biweekly-contest-33

A

Statement

简体中文English

Metadata

Link: 千位分隔数
Difficulty: Easy
Tag: 字符串

给你一个整数 n，请你每隔三位添加点（即 "." 符号）作为千位分隔符，并将结果以字符串格式返回。

示例 1：

输入：n = 987
输出："987"

示例 2：

输入：n = 1234
输出："1.234"

示例 3：

输入：n = 123456789
输出："123.456.789"

示例 4：

输入：n = 0
输出："0"

提示：

0 <= n < 2^31

Metadata

Link: Thousand Separator
Difficulty: Easy
Tag: String

Given an integer n, add a dot (".") as the thousands separator and return it in string format.

Example 1:

Input: n = 987
Output: "987"

Example 2:

Input: n = 1234
Output: "1.234"

Constraints:

0 <= n <= 2³¹ - 1

Solution

C++

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
// int n;

class Solution {
public:
    string thousandSeparator(int n) {
        int x = n;
        if (!x)
            return "0";
        vector<int> vec;
        while (x) {
            vec.push_back(x % 10);
            x /= 10;
        }
        //		reverse(all(vec));
        string res = "";
        for (int i = 0; i < SZ(vec); ++i) {
            if (i && i % 3 == 0)
                res += ".";
            res += vec[i] + '0';
        }
        reverse(all(res));
        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

简体中文English

Metadata

Link: 可以到达所有点的最少点数目
Difficulty: Medium
Tag: 图

给你一个 有向无环图 ， n 个节点编号为 0 到 n-1 ，以及一个边数组 edges ，其中 edges[i] = [from_i, to_i] 表示一条从点 from_i 到点 to_i 的有向边。

找到最小的点集使得从这些点出发能到达图中所有点。题目保证解存在且唯一。

你可以以任意顺序返回这些节点编号。

示例 1：

输入：n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
输出：[0,3]
解释：从单个节点出发无法到达所有节点。从 0 出发我们可以到达 [0,1,2,5] 。从 3 出发我们可以到达 [3,4,2,5] 。所以我们输出 [0,3] 。

示例 2：

输入：n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
输出：[0,2,3]
解释：注意到节点 0，3 和 2 无法从其他节点到达，所以我们必须将它们包含在结果点集中，这些点都能到达节点 1 和 4 。

提示：

2 <= n <= 10^5
1 <= edges.length <= min(10^5, n * (n - 1) / 2)
edges[i].length == 2
0 <= from_i, to_i < n
所有点对 (from_i, to_i) 互不相同。

Metadata

Link: Minimum Number of Vertices to Reach All Nodes
Difficulty: Medium
Tag: Graph

Given a directed acyclic graph, with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [from_i, to_i] represents a directed edge from node from_i to node to_i.

Find the smallest set of vertices from which all nodes in the graph are reachable. It's guaranteed that a unique solution exists.

Notice that you can return the vertices in any order.

Example 1:


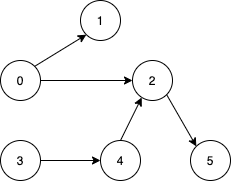
Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
Output: [0,3]
Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].

Example 2:


Input: n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
Output: [0,2,3]
Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.

Constraints:

2 <= n <= 10^5
1 <= edges.length <= min(10^5, n * (n - 1) / 2)
edges[i].length == 2
0 <= from_i, to_i < n
All pairs (from_i, to_i) are distinct.

Solution

C++

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
// int n;
int d[N];

class Solution {
public:
    vector<int> findSmallestSetOfVertices(int n, vector<vector<int>> &edges) {
        for (int i = 0; i <= n; ++i) d[i] = 0;
        for (auto &it : edges) {
            int u = it[0], v = it[1];
            ++d[v];
        }
        vector<int> res;
        for (int i = 0; i < n; ++i)
            if (!d[i])
                res.push_back(i);
        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

简体中文English

Metadata

Link: 得到目标数组的最少函数调用次数
Difficulty: Medium
Tag: 贪心 数组

给你一个与 nums 大小相同且初始值全为 0 的数组 arr ，请你调用以上函数得到整数数组 nums 。

请你返回将 arr 变成 nums 的最少函数调用次数。

答案保证在 32 位有符号整数以内。

示例 1：

输入：nums = [1,5]
输出：5
解释：给第二个数加 1 ：[0, 0] 变成 [0, 1] （1 次操作）。
将所有数字乘以 2 ：[0, 1] -> [0, 2] -> [0, 4] （2 次操作）。
给两个数字都加 1 ：[0, 4] -> [1, 4] -> [1, 5] （2 次操作）。
总操作次数为：1 + 2 + 2 = 5 。

示例 2：

输入：nums = [2,2]
输出：3
解释：给两个数字都加 1 ：[0, 0] -> [0, 1] -> [1, 1] （2 次操作）。
将所有数字乘以 2 ： [1, 1] -> [2, 2] （1 次操作）。
总操作次数为： 2 + 1 = 3 。

示例 3：

输入：nums = [4,2,5]
输出：6
解释：（初始）[0,0,0] -> [1,0,0] -> [1,0,1] -> [2,0,2] -> [2,1,2] -> [4,2,4] -> [4,2,5] （nums 数组）。

示例 4：

输入：nums = [3,2,2,4]
输出：7

示例 5：

输入：nums = [2,4,8,16]
输出：8

提示：

1 <= nums.length <= 10^5
0 <= nums[i] <= 10^9

Metadata

Link: Minimum Numbers of Function Calls to Make Target Array
Difficulty: Medium
Tag: Greedy Array

You are given an integer array nums. You have an integer array arr of the same length with all values set to 0 initially. You also have the following modify function:

You want to use the modify function to covert arr to nums using the minimum number of calls.

Return the minimum number of function calls to make nums from arr.

The test cases are generated so that the answer fits in a 32-bit signed integer.

Example 1:

Input: nums = [1,5]
Output: 5
Explanation: Increment by 1 (second element): [0, 0] to get [0, 1] (1 operation).
Double all the elements: [0, 1] -> [0, 2] -> [0, 4] (2 operations).
Increment by 1 (both elements)  [0, 4] -> [1, 4] -> [1, 5] (2 operations).
Total of operations: 1 + 2 + 2 = 5.

Example 2:

Input: nums = [2,2]
Output: 3
Explanation: Increment by 1 (both elements) [0, 0] -> [0, 1] -> [1, 1] (2 operations).
Double all the elements: [1, 1] -> [2, 2] (1 operation).
Total of operations: 2 + 1 = 3.

Example 3:

Input: nums = [4,2,5]
Output: 6
Explanation: (initial)[0,0,0] -> [1,0,0] -> [1,0,1] -> [2,0,2] -> [2,1,2] -> [4,2,4] -> [4,2,5](nums).

Constraints:

1 <= nums.length <= 10⁵
0 <= nums[i] <= 10⁹

Solution

C++

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
// int n;

class Solution {
public:
    int minOperations(vector<int> &nums) {
        ll res = 0;
        int Max = 0;
        for (auto &it : nums) {
            int now = 0;
            while (it) {
                if (it % 2 == 0) {
                    ++now;
                    it /= 2;
                } else {
                    ++res;
                    --it;
                }
            }
            chmax(Max, now);
        }
        return res + Max;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

D

Statement

简体中文English

Metadata

Link: 二维网格图中探测环
Difficulty: Medium
Tag: 深度优先搜索 广度优先搜索 并查集 数组 矩阵

给你一个二维字符网格数组 grid ，大小为 m x n ，你需要检查 grid 中是否存在 相同值 形成的环。

一个环是一条开始和结束于同一个格子的长度 大于等于 4 的路径。对于一个给定的格子，你可以移动到它上、下、左、右四个方向相邻的格子之一，可以移动的前提是这两个格子有 相同的值 。

同时，你也不能回到上一次移动时所在的格子。比方说，环 (1, 1) -> (1, 2) -> (1, 1) 是不合法的，因为从 (1, 2) 移动到 (1, 1) 回到了上一次移动时的格子。

如果 grid 中有相同值形成的环，请你返回 true ，否则返回 false 。

示例 1：

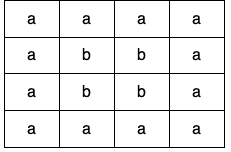
输入：grid = [["a","a","a","a"],["a","b","b","a"],["a","b","b","a"],["a","a","a","a"]]
输出：true
解释：如下图所示，有 2 个用不同颜色标出来的环：

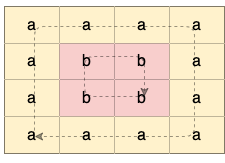
示例 2：

输入：grid = [["c","c","c","a"],["c","d","c","c"],["c","c","e","c"],["f","c","c","c"]]
输出：true
解释：如下图所示，只有高亮所示的一个合法环：

示例 3：

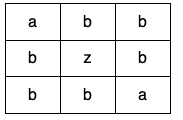
输入：grid = [["a","b","b"],["b","z","b"],["b","b","a"]]
输出：false

提示：

m == grid.length
n == grid[i].length
1 <= m <= 500
1 <= n <= 500
grid 只包含小写英文字母。

Metadata

Link: Detect Cycles in 2D Grid
Difficulty: Medium
Tag: Depth-First Search Breadth-First Search Union Find Array Matrix

Given a 2D array of characters grid of size m x n, you need to find if there exists any cycle consisting of the same value in grid.

A cycle is a path of length 4 or more in the grid that starts and ends at the same cell. From a given cell, you can move to one of the cells adjacent to it - in one of the four directions (up, down, left, or right), if it has the same value of the current cell.

Also, you cannot move to the cell that you visited in your last move. For example, the cycle (1, 1) -> (1, 2) -> (1, 1) is invalid because from (1, 2) we visited (1, 1) which was the last visited cell.

Return true if any cycle of the same value exists in grid, otherwise, return false.

Example 1:

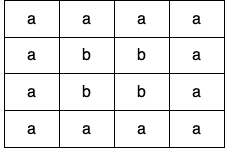
Input: grid = [["a","a","a","a"],["a","b","b","a"],["a","b","b","a"],["a","a","a","a"]]
Output: true
Explanation: There are two valid cycles shown in different colors in the image below:

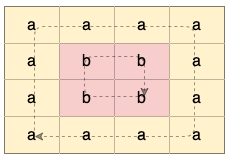
Example 2:

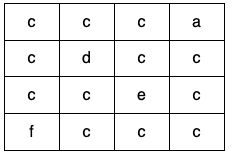
Input: grid = [["c","c","c","a"],["c","d","c","c"],["c","c","e","c"],["f","c","c","c"]]
Output: true
Explanation: There is only one valid cycle highlighted in the image below:

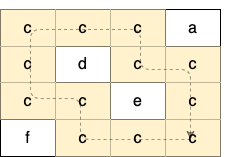
Example 3:

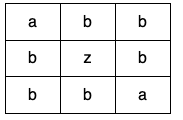
Input: grid = [["a","b","b"],["b","z","b"],["b","b","a"]]
Output: false

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 500
grid consists only of lowercase English letters.

Solution

C++

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 500 * 500 + 10;
int n, m;
vector<vector<int>> G;
int Move[4][2] = {-1, 0, 1, 0, 0, 1, 0, -1};
int vis[N], fa[N], g[510][510];
int has;

void dfs(int u) {
    vis[u] = 1;
    for (auto &v : G[u])
        if (v != fa[u]) {
            fa[v] = u;
            if (vis[v]) {
                has = 1;
                return;
            }
            dfs(v);
            if (has)
                return;
        }
}

bool valid(int x, int y) {
    if (x < 0 || x > n || y < 0 || y > m)
        return false;
    return true;
}

bool ok(vector<pII> &vec) {
    int _n = SZ(vec);
    G.clear();
    G.resize(_n + 1);
    for (int i = 0; i < _n; ++i) {
        g[vec[i].fi][vec[i].se] = i + 1;
        vis[i + 1] = 0;
        fa[i + 1] = 0;
    }
    has = 0;
    //	pt("-----");
    for (int i = 0; i < _n; ++i) {
        int x = vec[i].fi, y = vec[i].se, u = i + 1;
        for (int j = 0; j < 4; ++j) {
            int nx = x + Move[j][0];
            int ny = y + Move[j][1];
            if (valid(nx, ny) && g[nx][ny]) {
                int v = g[nx][ny];
                G[u].push_back(v);
                //	pt(u, v);
            }
        }
    }
    //	pt("-----------");
    for (int i = 0; i < _n; ++i) {
        g[vec[i].fi][vec[i].se] = 0;
    }
    for (int i = 1; i <= _n; ++i) {
        if (!vis[i]) {
            dfs(i);
            //	if (has) pt(i);
            if (has)
                return true;
        }
    }
    return false;
}

class Solution {
public:
    bool containsCycle(vector<vector<char>> &grid) {
        n = SZ(grid);
        m = SZ(grid[0]);
        for (int i = 0; i <= n; ++i)
            for (int j = 0; j <= m; ++j) g[i][j] = 0;
        vector<pII> vec[30];
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                vec[grid[i][j] - 'a'].push_back(pII(i, j));
            }
        }
        for (int i = 0; i < 26; ++i) {
            if (SZ(vec[i]) && ok(vec[i]))
                return true;
        }
        return false;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

最后更新: October 11, 2023