weekly-contest-306
A
Statement
Metadata
- Link: 矩阵中的局部最大值
- Difficulty: Easy
- Tag:
给你一个大小为 n x n 的整数矩阵 grid 。
生成一个大小为 (n - 2) x (n - 2) 的整数矩阵 maxLocal ,并满足:
maxLocal[i][j]等于grid中以i + 1行和j + 1列为中心的3 x 3矩阵中的 最大值 。
换句话说,我们希望找出 grid 中每个 3 x 3 矩阵中的最大值。
返回生成的矩阵。
示例 1:
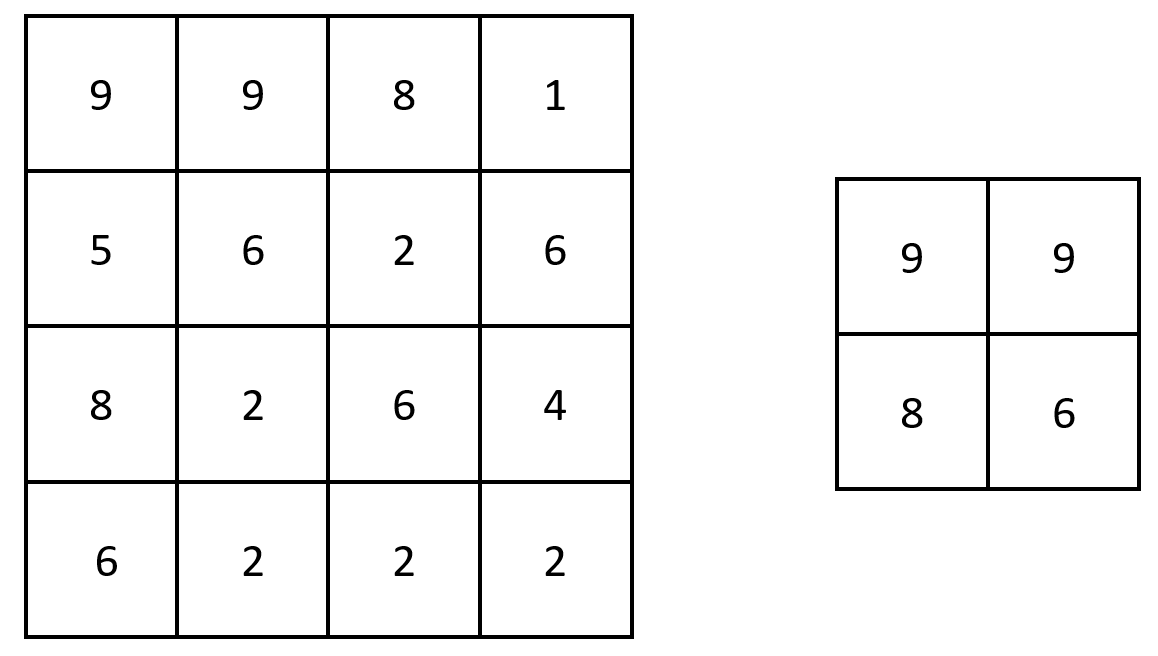
输入:grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]
输出:[[9,9],[8,6]]
解释:原矩阵和生成的矩阵如上图所示。
注意,生成的矩阵中,每个值都对应 grid 中一个相接的 3 x 3 矩阵的最大值。示例 2:
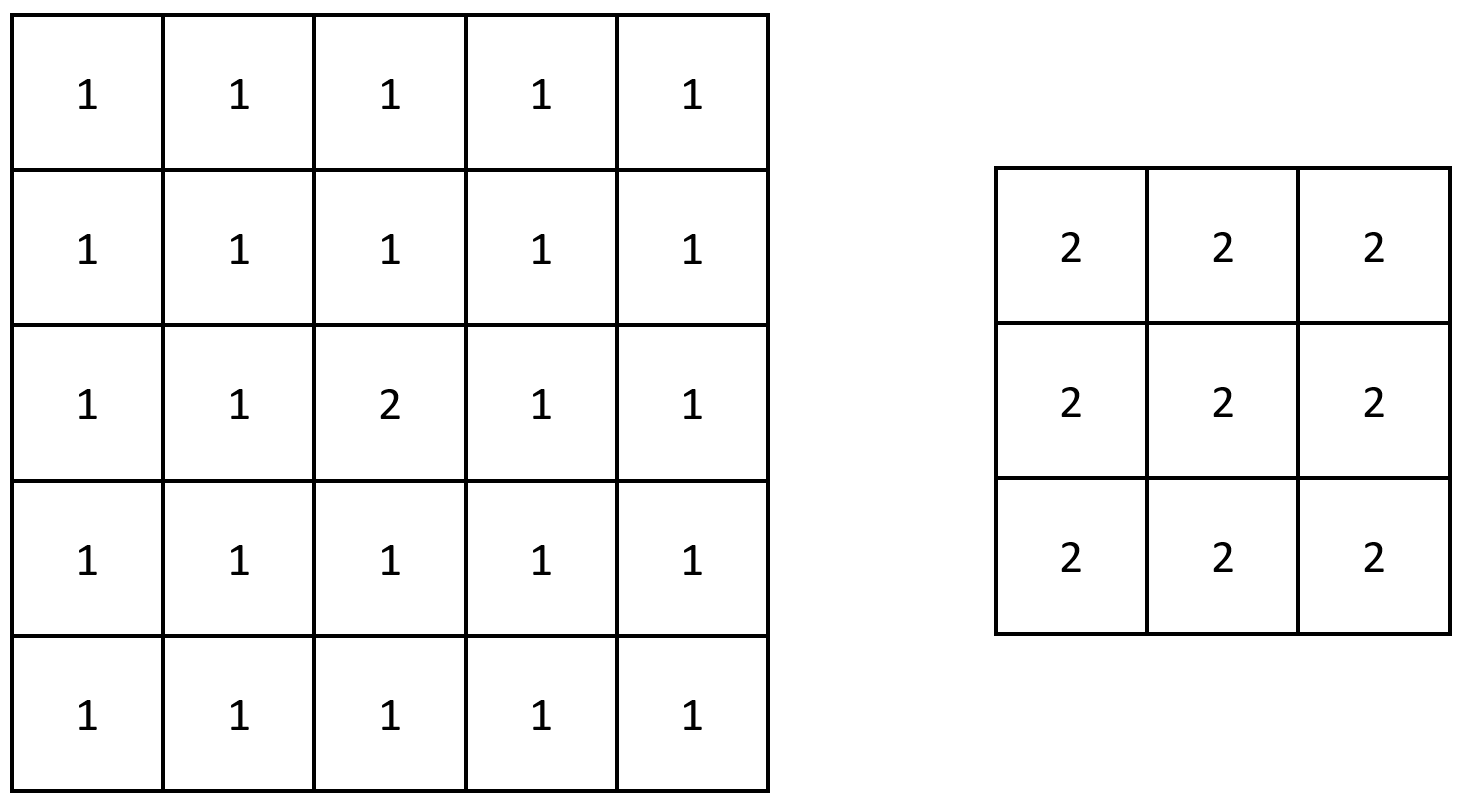
输入:grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]
输出:[[2,2,2],[2,2,2],[2,2,2]]
解释:注意,2 包含在 grid 中每个 3 x 3 的矩阵中。
提示:
n == grid.length == grid[i].length3 <= n <= 1001 <= grid[i][j] <= 100
Metadata
- Link: Largest Local Values in a Matrix
- Difficulty: Easy
- Tag:
You are given an n x n integer matrix grid.
Generate an integer matrix maxLocal of size (n - 2) x (n - 2) such that:
maxLocal[i][j]is equal to the largest value of the3 x 3matrix ingridcentered around rowi + 1and columnj + 1.
In other words, we want to find the largest value in every contiguous 3 x 3 matrix in grid.
Return the generated matrix.
Example 1:

Input: grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]
Output: [[9,9],[8,6]]
Explanation: The diagram above shows the original matrix and the generated matrix.
Notice that each value in the generated matrix corresponds to the largest value of a contiguous 3 x 3 matrix in grid.Example 2:

Input: grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]
Output: [[2,2,2],[2,2,2],[2,2,2]]
Explanation: Notice that the 2 is contained within every contiguous 3 x 3 matrix in grid.
Constraints:
n == grid.length == grid[i].length3 <= n <= 1001 <= grid[i][j] <= 100
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
vector<vector<int>> largestLocal(vector<vector<int>> &grid) {
int n = int(grid.size());
int m = n - 2;
auto res = vector<vector<int>>(m, vector<int>(m, 0));
for (int i = 0; i < n - 2; i++) {
for (int j = 0; j < n - 2; j++) {
int max_ = 0;
for (int k = 0; k < 3; k++) {
for (int l = 0; l < 3; l++) {
max_ = max(max_, grid[i + k][j + l]);
}
}
res[i][j] = max_;
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 边积分最高的节点
- Difficulty: Medium
- Tag:
给你一个有向图,图中有 n 个节点,节点编号从 0 到 n - 1 ,其中每个节点都 恰有一条 出边。
图由一个下标从 0 开始、长度为 n 的整数数组 edges 表示,其中 edges[i] 表示存在一条从节点 i 到节点 edges[i] 的 有向 边。
节点 i 的 边积分 定义为:所有存在一条指向节点 i 的边的节点的 编号 总和。
返回 边积分 最高的节点。如果多个节点的 边积分 相同,返回编号 最小 的那个。
示例 1:
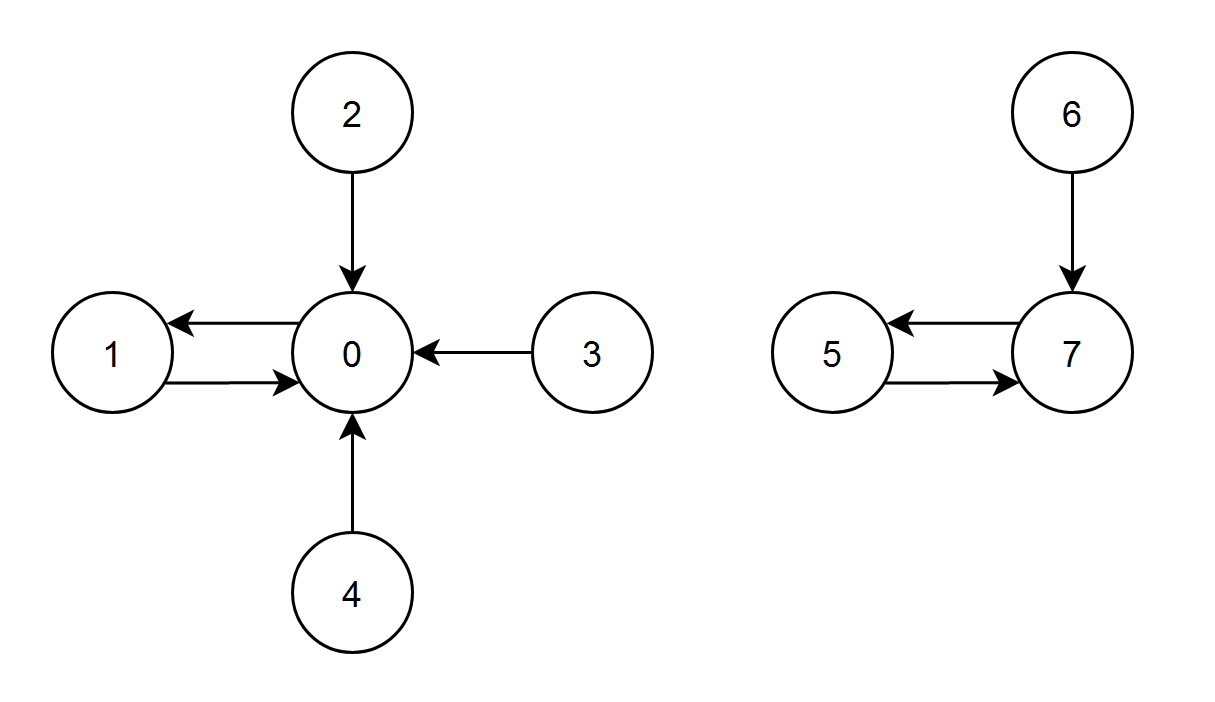
输入:edges = [1,0,0,0,0,7,7,5]
输出:7
解释:
- 节点 1、2、3 和 4 都有指向节点 0 的边,节点 0 的边积分等于 1 + 2 + 3 + 4 = 10 。
- 节点 0 有一条指向节点 1 的边,节点 1 的边积分等于 0 。
- 节点 7 有一条指向节点 5 的边,节点 5 的边积分等于 7 。
- 节点 5 和 6 都有指向节点 7 的边,节点 7 的边积分等于 5 + 6 = 11 。
节点 7 的边积分最高,所以返回 7 。
示例 2:
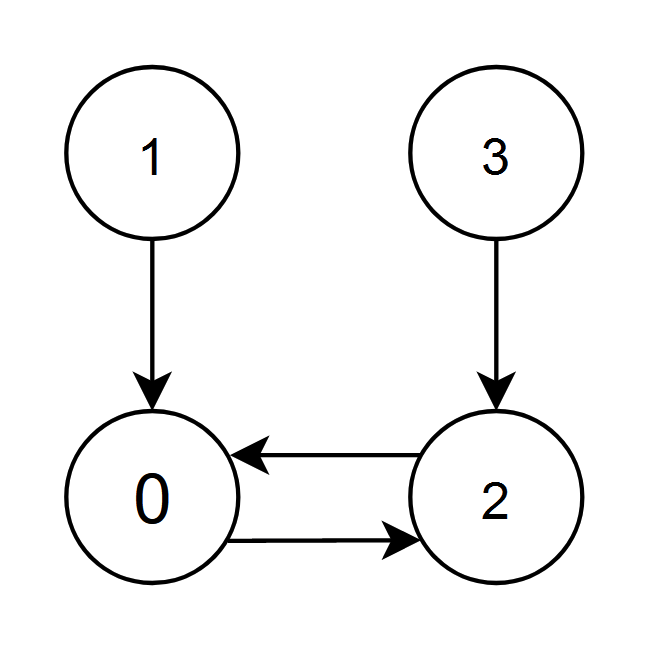
输入:edges = [2,0,0,2]
输出:0
解释:
- 节点 1 和 2 都有指向节点 0 的边,节点 0 的边积分等于 1 + 2 = 3 。
- 节点 0 和 3 都有指向节点 2 的边,节点 2 的边积分等于 0 + 3 = 3 。
节点 0 和 2 的边积分都是 3 。由于节点 0 的编号更小,返回 0 。
提示:
n == edges.length2 <= n <= 1050 <= edges[i] < nedges[i] != i
Metadata
- Link: Node With Highest Edge Score
- Difficulty: Medium
- Tag:
You are given a directed graph with n nodes labeled from 0 to n - 1, where each node has exactly one outgoing edge.
The graph is represented by a given 0-indexed integer array edges of length n, where edges[i] indicates that there is a directed edge from node i to node edges[i].
The edge score of a node i is defined as the sum of the labels of all the nodes that have an edge pointing to i.
Return the node with the highest edge score. If multiple nodes have the same edge score, return the node with the smallest index.
Example 1:

Input: edges = [1,0,0,0,0,7,7,5]
Output: 7
Explanation:
- The nodes 1, 2, 3 and 4 have an edge pointing to node 0. The edge score of node 0 is 1 + 2 + 3 + 4 = 10.
- The node 0 has an edge pointing to node 1. The edge score of node 1 is 0.
- The node 7 has an edge pointing to node 5. The edge score of node 5 is 7.
- The nodes 5 and 6 have an edge pointing to node 7. The edge score of node 7 is 5 + 6 = 11.
Node 7 has the highest edge score so return 7.
Example 2:

Input: edges = [2,0,0,2]
Output: 0
Explanation:
- The nodes 1 and 2 have an edge pointing to node 0. The edge score of node 0 is 1 + 2 = 3.
- The nodes 0 and 3 have an edge pointing to node 2. The edge score of node 2 is 0 + 3 = 3.
Nodes 0 and 2 both have an edge score of 3. Since node 0 has a smaller index, we return 0.
Constraints:
n == edges.length2 <= n <= 1050 <= edges[i] < nedges[i] != i
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int edgeScore(vector<int> &edges) {
int n = int(edges.size());
ll _max = 0;
int res = -1;
auto f = vector<ll>(n, 0);
for (int i = 0; i < n; i++) {
int x = edges[i];
f[x] += i;
}
for (int i = 0; i < n; i++) {
if (f[i] > _max) {
_max = f[i];
res = i;
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 根据模式串构造最小数字
- Difficulty: Medium
- Tag:
给你下标从 0 开始、长度为 n 的字符串 pattern ,它包含两种字符,'I' 表示 上升 ,'D' 表示 下降 。
你需要构造一个下标从 0 开始长度为 n + 1 的字符串,且它要满足以下条件:
num包含数字'1'到'9',其中每个数字 至多 使用一次。- 如果
pattern[i] == 'I',那么num[i] < num[i + 1]。 - 如果
pattern[i] == 'D',那么num[i] > num[i + 1]。
请你返回满足上述条件字典序 最小 的字符串 num。
示例 1:
输入:pattern = "IIIDIDDD"
输出:"123549876"
解释:
下标 0 ,1 ,2 和 4 处,我们需要使 num[i] < num[i+1] 。
下标 3 ,5 ,6 和 7 处,我们需要使 num[i] > num[i+1] 。
一些可能的 num 的值为 "245639871" ,"135749862" 和 "123849765" 。
"123549876" 是满足条件最小的数字。
注意,"123414321" 不是可行解因为数字 '1' 使用次数超过 1 次。示例 2:
输入:pattern = "DDD"
输出:"4321"
解释:
一些可能的 num 的值为 "9876" ,"7321" 和 "8742" 。
"4321" 是满足条件最小的数字。
提示:
1 <= pattern.length <= 8pattern只包含字符'I'和'D'。
Metadata
- Link: Construct Smallest Number From DI String
- Difficulty: Medium
- Tag:
You are given a 0-indexed string pattern of length n consisting of the characters 'I' meaning increasing and 'D' meaning decreasing.
A 0-indexed string num of length n + 1 is created using the following conditions:
numconsists of the digits'1'to'9', where each digit is used at most once.- If
pattern[i] == 'I', thennum[i] < num[i + 1]. - If
pattern[i] == 'D', thennum[i] > num[i + 1].
Return the lexicographically smallest possible string num that meets the conditions.
Example 1:
Input: pattern = "IIIDIDDD"
Output: "123549876"
Explanation:
At indices 0, 1, 2, and 4 we must have that num[i] < num[i+1].
At indices 3, 5, 6, and 7 we must have that num[i] > num[i+1].
Some possible values of num are "245639871", "135749862", and "123849765".
It can be proven that "123549876" is the smallest possible num that meets the conditions.
Note that "123414321" is not possible because the digit '1' is used more than once.Example 2:
Input: pattern = "DDD"
Output: "4321"
Explanation:
Some possible values of num are "9876", "7321", and "8742".
It can be proven that "4321" is the smallest possible num that meets the conditions.
Constraints:
1 <= pattern.length <= 8patternconsists of only the letters'I'and'D'.
Solution
#include <bits/stdc++.h>
#include <algorithm>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
string smallestNumber(string pattern) {
int n = int(pattern.size()) + 1;
auto f = vector<int>(n, 0);
for (int i = 1; i <= n; i++) {
f[i - 1] = i;
}
string res = "";
for (int i = n - 1; i >= 0; i--) {
res += to_string(i + 1);
}
do {
bool ok = true;
for (int i = 0; i < n - 1; i++) {
if (pattern[i] == 'I') {
if (f[i] > f[i + 1]) {
ok = false;
break;
}
} else {
if (f[i] < f[i + 1]) {
ok = false;
break;
}
}
}
if (ok) {
string _res = "";
for (const auto &i : f) {
_res += to_string(i);
}
res = min(res, _res);
break;
}
} while (next_permutation(f.begin(), f.end()));
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 统计特殊整数
- Difficulty: Hard
- Tag:
如果一个正整数每一个数位都是 互不相同 的,我们称它是 特殊整数 。
给你一个 正 整数 n ,请你返回区间 [1, n] 之间特殊整数的数目。
示例 1:
输入:n = 20
输出:19
解释:1 到 20 之间所有整数除了 11 以外都是特殊整数。所以总共有 19 个特殊整数。
示例 2:
输入:n = 5
输出:5
解释:1 到 5 所有整数都是特殊整数。
示例 3:
输入:n = 135
输出:110
解释:从 1 到 135 总共有 110 个整数是特殊整数。
不特殊的部分数字为:22 ,114 和 131 。
提示:
1 <= n <= 2 * 109
Metadata
- Link: Count Special Integers
- Difficulty: Hard
- Tag:
We call a positive integer special if all of its digits are distinct.
Given a positive integer n, return the number of special integers that belong to the interval [1, n].
Example 1:
Input: n = 20
Output: 19
Explanation: All the integers from 1 to 20, except 11, are special. Thus, there are 19 special integers.
Example 2:
Input: n = 5
Output: 5
Explanation: All the integers from 1 to 5 are special.
Example 3:
Input: n = 135
Output: 110
Explanation: There are 110 integers from 1 to 135 that are special.
Some of the integers that are not special are: 22, 114, and 131.
Constraints:
1 <= n <= 2 * 109
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
// #include <debug.hpp>
#else
#define dbg(...)
#endif
// head
bool ok(int x) {
auto f = vector<int>(10, 0);
while (x) {
int y = x % 10;
++f[y];
if (f[y] > 1) {
return false;
}
x /= 10;
}
return true;
}
class Solution {
public:
inline static int f[] = {0, 168570, 229050, 289530, 350010, 410490, 470970, 531450, 591930, 652410, 712890, 733050,
733050, 753210, 773370, 793530, 813690, 833850, 854010, 874170, 894330, 914490, 934650, 934650, 954810,
974970, 995130, 1015290, 1035450, 1055610, 1075770, 1095930, 1116090, 1136250, 1136250, 1156410, 1176570,
1196730, 1216890, 1237050, 1257210, 1277370, 1297530, 1317690, 1337850, 1337850, 1358010, 1378170, 1398330,
1418490, 1438650, 1458810, 1478970, 1499130, 1519290, 1539450, 1539450, 1559610, 1579770, 1599930, 1620090,
1640250, 1660410, 1680570, 1700730, 1720890, 1741050, 1741050, 1761210, 1781370, 1801530, 1821690, 1841850,
1862010, 1882170, 1902330, 1922490, 1942650, 1942650, 1962810, 1982970, 2003130, 2023290, 2043450, 2063610,
2083770, 2103930, 2124090, 2144250, 2144250, 2164410, 2184570, 2204730, 2224890, 2245050, 2265210, 2285370,
2305530, 2325690, 2345850, 2345850, 2345850, 2345850, 2350890, 2355930, 2360970, 2366010, 2371050, 2376090,
2381130, 2386170, 2386170, 2386170, 2386170, 2386170, 2386170, 2386170, 2386170, 2386170, 2386170, 2386170,
2391210, 2391210, 2391210, 2396250, 2401290, 2406330, 2411370, 2416410, 2421450, 2426490, 2431530, 2431530,
2436570, 2436570, 2441610, 2446650, 2451690, 2456730, 2461770, 2466810, 2471850, 2471850, 2476890, 2481930,
2481930, 2486970, 2492010, 2497050, 2502090, 2507130, 2512170, 2512170, 2517210, 2522250, 2527290, 2527290,
2532330, 2537370, 2542410, 2547450, 2552490, 2552490, 2557530, 2562570, 2567610, 2572650, 2572650, 2577690,
2582730, 2587770, 2592810, 2592810, 2597850, 2602890, 2607930, 2612970, 2618010, 2618010, 2623050, 2628090,
2633130, 2633130, 2638170, 2643210, 2648250, 2653290, 2658330, 2663370, 2663370, 2668410, 2673450, 2673450,
2678490, 2683530, 2688570, 2693610, 2698650, 2703690, 2708730, 2708730, 2708730, 2713770, 2713770, 2718810,
2723850, 2728890, 2733930, 2738970, 2744010, 2749050, 2754090, 2754090, 2754090, 2759130, 2764170, 2769210,
2774250, 2779290, 2784330, 2789370, 2789370, 2789370, 2789370, 2789370, 2789370, 2789370, 2789370, 2789370,
2789370, 2789370, 2794410, 2799450, 2799450, 2799450, 2804490, 2809530, 2814570, 2819610, 2824650, 2829690,
2834730, 2839770, 2839770, 2844810, 2844810, 2849850, 2854890, 2859930, 2864970, 2870010, 2875050, 2880090,
2880090, 2885130, 2890170, 2890170, 2895210, 2900250, 2905290, 2910330, 2915370, 2920410, 2920410, 2925450,
2930490, 2935530, 2935530, 2940570, 2945610, 2950650, 2955690, 2960730, 2960730, 2965770, 2970810, 2975850,
2980890, 2980890, 2985930, 2990970, 2996010, 3001050, 3001050, 3006090, 3011130, 3016170, 3021210, 3026250,
3026250, 3031290, 3036330, 3041370, 3041370, 3046410, 3051450, 3056490, 3061530, 3066570, 3071610, 3071610,
3071610, 3076650, 3081690, 3081690, 3086730, 3091770, 3096810, 3101850, 3106890, 3111930, 3116970, 3116970,
3122010, 3122010, 3127050, 3132090, 3137130, 3142170, 3147210, 3152250, 3157290, 3162330, 3162330, 3162330,
3167370, 3172410, 3177450, 3182490, 3187530, 3192570, 3192570, 3192570, 3192570, 3192570, 3192570, 3192570,
3192570, 3192570, 3192570, 3192570, 3197610, 3202650, 3207690, 3207690, 3207690, 3212730, 3217770, 3222810,
3227850, 3232890, 3237930, 3242970, 3248010, 3248010, 3253050, 3253050, 3258090, 3263130, 3268170, 3273210,
3278250, 3283290, 3288330, 3288330, 3293370, 3298410, 3298410, 3303450, 3308490, 3313530, 3318570, 3323610,
3328650, 3328650, 3333690, 3338730, 3343770, 3343770, 3348810, 3353850, 3358890, 3363930, 3368970, 3368970,
3374010, 3379050, 3384090, 3389130, 3389130, 3394170, 3399210, 3404250, 3409290, 3409290, 3414330, 3419370,
3424410, 3429450, 3434490, 3434490, 3434490, 3439530, 3444570, 3449610, 3449610, 3454650, 3459690, 3464730,
3469770, 3474810, 3479850, 3479850, 3484890, 3489930, 3489930, 3494970, 3500010, 3505050, 3510090, 3515130,
3520170, 3525210, 3525210, 3530250, 3530250, 3535290, 3540330, 3545370, 3550410, 3555450, 3560490, 3565530,
3570570, 3570570, 3570570, 3575610, 3580650, 3585690, 3590730, 3595770, 3595770, 3595770, 3595770, 3595770,
3595770, 3595770, 3595770, 3595770, 3595770, 3595770, 3600810, 3605850, 3610890, 3615930, 3615930, 3615930,
3620970, 3626010, 3631050, 3636090, 3641130, 3646170, 3651210, 3656250, 3656250, 3661290, 3661290, 3666330,
3671370, 3676410, 3681450, 3686490, 3691530, 3696570, 3696570, 3701610, 3706650, 3706650, 3711690, 3716730,
3721770, 3726810, 3731850, 3736890, 3736890, 3741930, 3746970, 3752010, 3752010, 3757050, 3762090, 3767130,
3772170, 3777210, 3777210, 3782250, 3787290, 3792330, 3797370, 3797370, 3797370, 3802410, 3807450, 3812490,
3817530, 3817530, 3822570, 3827610, 3832650, 3837690, 3842730, 3842730, 3847770, 3852810, 3857850, 3857850,
3862890, 3867930, 3872970, 3878010, 3883050, 3888090, 3888090, 3893130, 3898170, 3898170, 3903210, 3908250,
3913290, 3918330, 3923370, 3928410, 3933450, 3933450, 3938490, 3938490, 3943530, 3948570, 3953610, 3958650,
3963690, 3968730, 3973770, 3978810, 3978810, 3978810, 3983850, 3988890, 3993930, 3998970, 3998970, 3998970,
3998970, 3998970, 3998970, 3998970, 3998970, 3998970, 3998970, 3998970, 4004010, 4009050, 4014090, 4019130,
4024170, 4024170, 4024170, 4029210, 4034250, 4039290, 4044330, 4049370, 4054410, 4059450, 4064490, 4064490,
4069530, 4069530, 4074570, 4079610, 4084650, 4089690, 4094730, 4099770, 4104810, 4104810, 4109850, 4114890,
4114890, 4119930, 4124970, 4130010, 4135050, 4140090, 4145130, 4145130, 4150170, 4155210, 4160250, 4160250,
4160250, 4165290, 4170330, 4175370, 4180410, 4185450, 4185450, 4190490, 4195530, 4200570, 4205610, 4205610,
4210650, 4215690, 4220730, 4225770, 4225770, 4230810, 4235850, 4240890, 4245930, 4250970, 4250970, 4256010,
4261050, 4266090, 4266090, 4271130, 4276170, 4281210, 4286250, 4291290, 4296330, 4296330, 4301370, 4306410,
4306410, 4311450, 4316490, 4321530, 4326570, 4331610, 4336650, 4341690, 4341690, 4346730, 4346730, 4351770,
4356810, 4361850, 4366890, 4371930, 4376970, 4382010, 4387050, 4387050, 4387050, 4392090, 4397130, 4402170,
4402170, 4402170, 4402170, 4402170, 4402170, 4402170, 4402170, 4402170, 4402170, 4402170, 4407210, 4412250,
4417290, 4422330, 4427370, 4432410, 4432410, 4432410, 4437450, 4442490, 4447530, 4452570, 4457610, 4462650,
4467690, 4472730, 4472730, 4477770, 4477770, 4482810, 4487850, 4492890, 4497930, 4502970, 4508010, 4513050,
4513050, 4518090, 4523130, 4523130, 4523130, 4528170, 4533210, 4538250, 4543290, 4548330, 4553370, 4553370,
4558410, 4563450, 4568490, 4568490, 4573530, 4578570, 4583610, 4588650, 4593690, 4593690, 4598730, 4603770,
4608810, 4613850, 4613850, 4618890, 4623930, 4628970, 4634010, 4634010, 4639050, 4644090, 4649130, 4654170,
4659210, 4659210, 4664250, 4669290, 4674330, 4674330, 4679370, 4684410, 4689450, 4694490, 4699530, 4704570,
4704570, 4709610, 4714650, 4714650, 4719690, 4724730, 4729770, 4734810, 4739850, 4744890, 4749930, 4749930,
4754970, 4754970, 4760010, 4765050, 4770090, 4775130, 4780170, 4785210, 4790250, 4795290, 4795290, 4795290,
4800330, 4805370, 4805370, 4805370, 4805370, 4805370, 4805370, 4805370, 4805370, 4805370, 4805370, 4805370,
4810410, 4815450, 4820490, 4825530, 4830570, 4835610, 4840650, 4840650, 4840650, 4845690, 4850730, 4855770,
4860810, 4865850, 4870890, 4875930, 4880970, 4880970, 4886010, 4886010, 4886010, 4891050, 4896090, 4901130,
4906170, 4911210, 4916250, 4921290, 4921290, 4926330, 4931370, 4931370, 4936410, 4941450, 4946490, 4951530,
4956570, 4961610, 4961610, 4966650, 4971690, 4976730, 4976730, 4981770, 4986810, 4991850, 4996890, 5001930,
5001930, 5006970, 5012010, 5017050, 5022090, 5022090, 5027130, 5032170, 5037210, 5042250, 5042250, 5047290,
5052330, 5057370, 5062410, 5067450, 5067450, 5072490, 5077530, 5082570, 5082570, 5087610, 5092650, 5097690,
5102730, 5107770, 5112810, 5112810, 5117850, 5122890, 5122890, 5127930, 5132970, 5138010, 5143050, 5148090,
5153130, 5158170, 5158170, 5163210, 5163210, 5168250, 5173290, 5178330, 5183370, 5188410, 5193450, 5198490,
5203530, 5203530, 5203530, 5208570, 5208570, 5208570, 5208570, 5208570, 5208570, 5208570, 5208570, 5208570,
5208570, 5208570, 5213610, 5218650, 5223690, 5228730, 5233770, 5238810, 5243850, 5248890, 5248890, 5248890,
5248890, 5253930, 5258970, 5264010, 5269050, 5274090, 5279130, 5284170, 5289210, 5289210, 5294250, 5294250,
5299290, 5304330, 5309370, 5314410, 5319450, 5324490, 5329530, 5329530, 5334570, 5339610, 5339610, 5344650,
5349690, 5354730, 5359770, 5364810, 5369850, 5369850, 5374890, 5379930, 5384970, 5384970, 5390010, 5395050,
5400090, 5405130, 5410170, 5410170, 5415210, 5420250, 5425290, 5430330, 5430330, 5435370, 5440410, 5445450,
5450490, 5450490, 5455530, 5460570, 5465610, 5470650, 5475690, 5475690, 5480730, 5485770, 5490810, 5490810,
5495850, 5500890, 5505930, 5510970, 5516010, 5521050, 5521050, 5526090, 5531130, 5531130, 5536170, 5541210,
5546250, 5551290, 5556330, 5561370, 5566410, 5566410, 5571450, 5571450, 5576490, 5581530, 5586570, 5591610,
5596650, 5601690, 5606730, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770,
5611770, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770,
5611770, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770, 5611770,
5611770, 5611770, 5611770, 5612490, 5613210, 5613930, 5614650, 5615370, 5616090, 5616810, 5616810, 5616810,
5617530, 5617530, 5618250, 5618970, 5619690, 5620410, 5621130, 5621850, 5621850, 5621850, 5622570, 5623290,
5623290, 5624010, 5624730, 5625450, 5626170, 5626890, 5626890, 5626890, 5627610, 5628330, 5629050, 5629050,
5629770, 5630490, 5631210, 5631930, 5631930, 5631930, 5632650, 5633370, 5634090, 5634810, 5634810, 5635530,
5636250, 5636970, 5636970, 5636970, 5637690, 5638410, 5639130, 5639850, 5640570, 5640570, 5641290, 5642010,
5642010, 5642010, 5642730, 5643450, 5644170, 5644890, 5645610, 5646330, 5646330, 5647050, 5647050, 5647050,
5647770, 5648490, 5649210, 5649930, 5650650, 5651370, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090,
5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090,
5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090,
5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090,
5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090,
5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090,
5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090,
5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090,
5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090, 5652090,
5652090, 5652090, 5652090, 5652810, 5653530, 5654250, 5654970, 5655690, 5656410, 5657130, 5657130, 5657130,
5657130, 5657130, 5657130, 5657130, 5657130, 5657130, 5657130, 5657130, 5657130, 5657130, 5657130, 5657130,
5657130, 5657130, 5657130, 5657130, 5657130, 5657130, 5657850, 5657850, 5657850, 5657850, 5658570, 5659290,
5660010, 5660730, 5661450, 5662170, 5662890, 5662890, 5662890, 5663610, 5663610, 5664330, 5665050, 5665770,
5666490, 5667210, 5667930, 5667930, 5667930, 5668650, 5669370, 5669370, 5670090, 5670810, 5671530, 5672250,
5672970, 5672970, 5672970, 5673690, 5674410, 5675130, 5675130, 5675850, 5676570, 5677290, 5678010, 5678010,
5678010, 5678730, 5679450, 5680170, 5680890, 5680890, 5681610, 5682330, 5683050, 5683050, 5683050, 5683770,
5684490, 5685210, 5685930, 5686650, 5686650, 5687370, 5688090, 5688090, 5688090, 5688810, 5689530, 5690250,
5690970, 5691690, 5692410, 5692410, 5692410, 5692410, 5693130, 5693130, 5693850, 5694570, 5695290, 5696010,
5696730, 5697450, 5697450, 5697450, 5697450, 5697450, 5697450, 5697450, 5697450, 5697450, 5697450, 5697450,
5698170, 5698170, 5698170, 5698170, 5698890, 5699610, 5700330, 5701050, 5701770, 5702490, 5702490, 5702490,
5702490, 5702490, 5702490, 5702490, 5702490, 5702490, 5702490, 5702490, 5703210, 5703210, 5703930, 5703930,
5703930, 5704650, 5705370, 5706090, 5706810, 5707530, 5708250, 5708250, 5708970, 5708970, 5709690, 5709690,
5710410, 5711130, 5711850, 5712570, 5713290, 5713290, 5714010, 5714010, 5714730, 5715450, 5715450, 5716170,
5716890, 5717610, 5718330, 5718330, 5719050, 5719050, 5719770, 5720490, 5721210, 5721210, 5721930, 5722650,
5723370, 5723370, 5724090, 5724090, 5724810, 5725530, 5726250, 5726970, 5726970, 5727690, 5728410, 5728410,
5729130, 5729130, 5729850, 5730570, 5731290, 5732010, 5732730, 5732730, 5732730, 5732730, 5733450, 5734170,
5734170, 5734890, 5735610, 5736330, 5737050, 5737770, 5737770, 5737770, 5737770, 5737770, 5737770, 5737770,
5737770, 5737770, 5737770, 5737770, 5738490, 5738490, 5738490, 5739210, 5739210, 5739930, 5740650, 5741370,
5742090, 5742810, 5743530, 5743530, 5744250, 5744250, 5744250, 5744970, 5745690, 5746410, 5747130, 5747850,
5747850, 5747850, 5747850, 5747850, 5747850, 5747850, 5747850, 5747850, 5747850, 5747850, 5748570, 5748570,
5749290, 5750010, 5750010, 5750010, 5750730, 5751450, 5752170, 5752890, 5753610, 5753610, 5754330, 5755050,
5755050, 5755770, 5755770, 5756490, 5757210, 5757930, 5758650, 5758650, 5759370, 5760090, 5760090, 5760810,
5761530, 5761530, 5762250, 5762970, 5763690, 5763690, 5764410, 5765130, 5765130, 5765850, 5766570, 5767290,
5767290, 5768010, 5768730, 5768730, 5769450, 5770170, 5770170, 5770890, 5771610, 5772330, 5773050, 5773050,
5773050, 5773050, 5773770, 5774490, 5775210, 5775210, 5775930, 5776650, 5777370, 5778090, 5778090, 5778090,
5778090, 5778090, 5778090, 5778090, 5778090, 5778090, 5778090, 5778090, 5778810, 5778810, 5778810, 5779530,
5780250, 5780250, 5780970, 5781690, 5782410, 5783130, 5783850, 5783850, 5784570, 5784570, 5785290, 5785290,
5786010, 5786730, 5787450, 5788170, 5788890, 5788890, 5789610, 5790330, 5790330, 5790330, 5791050, 5791770,
5792490, 5793210, 5793210, 5793210, 5793210, 5793210, 5793210, 5793210, 5793210, 5793210, 5793210, 5793210,
5793930, 5793930, 5794650, 5795370, 5796090, 5796090, 5796090, 5796810, 5797530, 5798250, 5798970, 5798970,
5799690, 5800410, 5801130, 5801130, 5801850, 5801850, 5802570, 5803290, 5804010, 5804010, 5804730, 5805450,
5806170, 5806170, 5806890, 5807610, 5807610, 5808330, 5809050, 5809050, 5809770, 5810490, 5811210, 5811210,
5811930, 5812650, 5813370, 5813370, 5813370, 5813370, 5814090, 5814810, 5815530, 5816250, 5816250, 5816970,
5817690, 5818410, 5818410, 5818410, 5818410, 5818410, 5818410, 5818410, 5818410, 5818410, 5818410, 5818410,
5819130, 5819130, 5819130, 5819850, 5820570, 5821290, 5821290, 5822010, 5822730, 5823450, 5824170, 5824170,
5824890, 5824890, 5825610, 5826330, 5826330, 5827050, 5827770, 5828490, 5829210, 5829210, 5829930, 5830650,
5830650, 5831370, 5831370, 5832090, 5832810, 5833530, 5834250, 5834250, 5834970, 5835690, 5836410, 5836410,
5836410, 5837130, 5837850, 5838570, 5838570, 5838570, 5838570, 5838570, 5838570, 5838570, 5838570, 5838570,
5838570, 5838570, 5839290, 5839290, 5840010, 5840730, 5841450, 5842170, 5842170, 5842170, 5842890, 5843610,
5844330, 5844330, 5845050, 5845770, 5846490, 5847210, 5847210, 5847930, 5847930, 5848650, 5849370, 5849370,
5850090, 5850810, 5851530, 5852250, 5852250, 5852970, 5853690, 5853690, 5853690, 5853690, 5854410, 5855130,
5855850, 5856570, 5857290, 5857290, 5858010, 5858730, 5858730, 5858730, 5858730, 5858730, 5858730, 5858730,
5858730, 5858730, 5858730, 5858730, 5859450, 5859450, 5859450, 5860170, 5860890, 5861610, 5862330, 5862330,
5863050, 5863770, 5864490, 5864490, 5865210, 5865210, 5865930, 5866650, 5867370, 5867370, 5868090, 5868810,
5869530, 5869530, 5870250, 5870970, 5870970, 5871690, 5872410, 5872410, 5873130, 5873850, 5874570, 5874570,
5875290, 5876010, 5876730, 5876730, 5877450, 5877450, 5878170, 5878890, 5879610, 5879610, 5880330, 5881050,
5881770, 5882490, 5882490, 5882490, 5883210, 5883930, 5883930, 5883930, 5883930, 5883930, 5883930, 5883930,
5883930, 5883930, 5883930, 5883930, 5884650, 5884650, 5885370, 5886090, 5886810, 5887530, 5888250, 5888250,
5888250, 5888970, 5889690, 5889690, 5890410, 5891130, 5891850, 5892570, 5893290, 5893290, 5894010, 5894010,
5894010, 5894010, 5894730, 5895450, 5896170, 5896890, 5897610, 5898330, 5898330, 5899050, 5899050, 5899050,
5899050, 5899050, 5899050, 5899050, 5899050, 5899050, 5899050, 5899050, 5899770, 5899770, 5899770, 5900490,
5901210, 5901930, 5902650, 5903370, 5903370, 5904090, 5904810, 5904810, 5905530, 5905530, 5906250, 5906970,
5907690, 5908410, 5908410, 5909130, 5909850, 5909850, 5910570, 5911290, 5911290, 5912010, 5912730, 5913450,
5913450, 5914170, 5914890, 5914890, 5915610, 5916330, 5917050, 5917050, 5917770, 5918490, 5918490, 5919210,
5919930, 5919930, 5920650, 5921370, 5922090, 5922810, 5922810, 5923530, 5923530, 5924250, 5924970, 5924970,
5925690, 5926410, 5927130, 5927850, 5928570, 5928570, 5928570, 5929290, 5929290, 5929290, 5929290, 5929290,
5929290, 5929290, 5929290, 5929290, 5929290, 5929290, 5930010, 5930010, 5930730, 5931450, 5932170, 5932890,
5933610, 5934330, 5934330, 5934330, 5934330, 5934330, 5935050, 5935770, 5936490, 5937210, 5937930, 5938650,
5939370, 5939370, 5939370, 5939370, 5939370, 5939370, 5939370, 5939370, 5939370, 5939370, 5939370, 5939370,
5940090, 5940090, 5940090, 5940810, 5941530, 5942250, 5942970, 5943690, 5944410, 5944410, 5945130, 5945130,
5945850, 5945850, 5946570, 5947290, 5948010, 5948730, 5949450, 5949450, 5950170, 5950170, 5950890, 5951610,
5951610, 5952330, 5953050, 5953770, 5954490, 5954490, 5955210, 5955210, 5955930, 5956650, 5957370, 5957370,
5958090, 5958810, 5959530, 5959530, 5960250, 5960250, 5960970, 5961690, 5962410, 5963130, 5963130, 5963850,
5964570, 5964570, 5965290, 5965290, 5966010, 5966730, 5967450, 5968170, 5968890, 5968890, 5969610, 5969610,
5970330, 5970330, 5971050, 5971770, 5972490, 5973210, 5973930, 5974650, 5974650, 5974650, 5974650, 5974650,
5974650, 5974650, 5974650, 5974650, 5974650, 5974650, 5974650, 5974650};
int countSpecialNumbers(int n) {
int x = n / 1000000;
int res = f[x];
for (int i = 1000000 * x + 1; i <= n; i++) {
if (ok(i)) {
++res;
}
}
return res;
}
};
#ifdef LOCAL
int main() {
int res = 0;
for (int i = 1, j = 1; i <= 2000000000; i++, j++) {
if (ok(i)) {
++res;
}
if (j == 1000000) {
j = 0;
cout << res << ",";
}
}
return 0;
}
#endif
Solution1
#include <bits/stdc++.h>
#include <cstring>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
// #include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int dp[20][2][2][2050];
bool init{false};
int dfs(int pos, int up, int pre_zero, int flag, vector<int> x) {
if (pos == 0) {
return !pre_zero;
}
int &res = dp[pos][up][pre_zero][flag];
if (res != -1) {
return res;
}
res = 0;
int current_up = x.back();
auto _x = x;
_x.pop_back();
for (int i = 0; i <= 9; i++) {
if (up && i > current_up) {
break;
}
int _flag = flag;
if (pre_zero && i == 0) {
} else {
_flag |= (1 << i);
if (_flag == flag) {
continue;
}
}
res += dfs(pos - 1, up && current_up == i, pre_zero && i == 0, _flag, _x);
}
return res;
}
int countSpecialNumbers(int n) {
if (!init) {
memset(dp, -1, sizeof dp);
init = true;
}
auto f = [](int x) {
int res = 0;
while (x) {
++res;
x /= 10;
}
return res;
};
auto g = [](int x) {
auto f = vector<int>();
while (x) {
f.push_back(x % 10);
x /= 10;
}
return f;
};
return dfs(f(n), 1, 1, 0, g(n));
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif