weekly-contest-318
A
Statement
Metadata
- Link: 对数组执行操作
- Difficulty: Easy
- Tag:
给你一个下标从 0 开始的数组 nums ,数组大小为 n ,且由 非负 整数组成。
你需要对数组执行 n - 1 步操作,其中第 i 步操作(从 0 开始计数)要求对 nums 中第 i 个元素执行下述指令:
- 如果
nums[i] == nums[i + 1],则nums[i]的值变成原来的2倍,nums[i + 1]的值变成0。否则,跳过这步操作。
在执行完 全部 操作后,将所有 0 移动 到数组的 末尾 。
- 例如,数组
[1,0,2,0,0,1]将所有0移动到末尾后变为[1,2,1,0,0,0]。
返回结果数组。
注意 操作应当 依次有序 执行,而不是一次性全部执行。
示例 1:
输入:nums = [1,2,2,1,1,0]
输出:[1,4,2,0,0,0]
解释:执行以下操作:
- i = 0: nums[0] 和 nums[1] 不相等,跳过这步操作。
- i = 1: nums[1] 和 nums[2] 相等,nums[1] 的值变成原来的 2 倍,nums[2] 的值变成 0 。数组变成 [1,4,0,1,1,0] 。
- i = 2: nums[2] 和 nums[3] 不相等,所以跳过这步操作。
- i = 3: nums[3] 和 nums[4] 相等,nums[3] 的值变成原来的 2 倍,nums[4] 的值变成 0 。数组变成 [1,4,0,2,0,0] 。
- i = 4: nums[4] 和 nums[5] 相等,nums[4] 的值变成原来的 2 倍,nums[5] 的值变成 0 。数组变成 [1,4,0,2,0,0] 。
执行完所有操作后,将 0 全部移动到数组末尾,得到结果数组 [1,4,2,0,0,0] 。
示例 2:
输入:nums = [0,1]
输出:[1,0]
解释:无法执行任何操作,只需要将 0 移动到末尾。
提示:
2 <= nums.length <= 20000 <= nums[i] <= 1000
Metadata
- Link: Apply Operations to an Array
- Difficulty: Easy
- Tag:
You are given a 0-indexed array nums of size n consisting of non-negative integers.
You need to apply n - 1 operations to this array where, in the ith operation (0-indexed), you will apply the following on the ith element of nums:
- If
nums[i] == nums[i + 1], then multiplynums[i]by2and setnums[i + 1]to0. Otherwise, you skip this operation.
After performing all the operations, shift all the 0's to the end of the array.
- For example, the array
[1,0,2,0,0,1]after shifting all its0's to the end, is[1,2,1,0,0,0].
Return the resulting array.
Note that the operations are applied sequentially, not all at once.
Example 1:
Input: nums = [1,2,2,1,1,0]
Output: [1,4,2,0,0,0]
Explanation: We do the following operations:
- i = 0: nums[0] and nums[1] are not equal, so we skip this operation.
- i = 1: nums[1] and nums[2] are equal, we multiply nums[1] by 2 and change nums[2] to 0. The array becomes [1,4,0,1,1,0].
- i = 2: nums[2] and nums[3] are not equal, so we skip this operation.
- i = 3: nums[3] and nums[4] are equal, we multiply nums[3] by 2 and change nums[4] to 0. The array becomes [1,4,0,2,0,0].
- i = 4: nums[4] and nums[5] are equal, we multiply nums[4] by 2 and change nums[5] to 0. The array becomes [1,4,0,2,0,0].
After that, we shift the 0's to the end, which gives the array [1,4,2,0,0,0].
Example 2:
Input: nums = [0,1]
Output: [1,0]
Explanation: No operation can be applied, we just shift the 0 to the end.
Constraints:
2 <= nums.length <= 20000 <= nums[i] <= 1000
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
vector<int> applyOperations(vector<int> &nums) {
int n = int(nums.size());
for (int i = 1; i < n; i++) {
if (nums[i - 1] == nums[i]) {
nums[i - 1] *= 2;
nums[i] = 0;
}
}
auto res = vector<int>();
int zero = 0;
for (int i = 0; i < n; i++) {
if (nums[i] == 0) {
++zero;
} else {
res.push_back(nums[i]);
}
}
if (zero) {
auto zero_vec = vector<int>(zero, 0);
res.insert(res.end(), all(zero_vec));
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 长度为 K 子数组中的最大和
- Difficulty: Medium
- Tag:
给你一个整数数组 nums 和一个整数 k 。请你从 nums 中满足下述条件的全部子数组中找出最大子数组和:
- 子数组的长度是
k,且 - 子数组中的所有元素 各不相同 。
返回满足题面要求的最大子数组和。如果不存在子数组满足这些条件,返回 0 。
子数组 是数组中一段连续非空的元素序列。
示例 1:
输入:nums = [1,5,4,2,9,9,9], k = 3
输出:15
解释:nums 中长度为 3 的子数组是:
- [1,5,4] 满足全部条件,和为 10 。
- [5,4,2] 满足全部条件,和为 11 。
- [4,2,9] 满足全部条件,和为 15 。
- [2,9,9] 不满足全部条件,因为元素 9 出现重复。
- [9,9,9] 不满足全部条件,因为元素 9 出现重复。
因为 15 是满足全部条件的所有子数组中的最大子数组和,所以返回 15 。
示例 2:
输入:nums = [4,4,4], k = 3
输出:0
解释:nums 中长度为 3 的子数组是:
- [4,4,4] 不满足全部条件,因为元素 4 出现重复。
因为不存在满足全部条件的子数组,所以返回 0 。
提示:
1 <= k <= nums.length <= 1051 <= nums[i] <= 105
Metadata
- Link: Maximum Sum of Distinct Subarrays With Length K
- Difficulty: Medium
- Tag:
You are given an integer array nums and an integer k. Find the maximum subarray sum of all the subarrays of nums that meet the following conditions:
- The length of the subarray is
k, and - All the elements of the subarray are distinct.
Return the maximum subarray sum of all the subarrays that meet the conditions. If no subarray meets the conditions, return 0.
A subarray is a contiguous non-empty sequence of elements within an array.
Example 1:
Input: nums = [1,5,4,2,9,9,9], k = 3
Output: 15
Explanation: The subarrays of nums with length 3 are:
- [1,5,4] which meets the requirements and has a sum of 10.
- [5,4,2] which meets the requirements and has a sum of 11.
- [4,2,9] which meets the requirements and has a sum of 15.
- [2,9,9] which does not meet the requirements because the element 9 is repeated.
- [9,9,9] which does not meet the requirements because the element 9 is repeated.
We return 15 because it is the maximum subarray sum of all the subarrays that meet the conditions
Example 2:
Input: nums = [4,4,4], k = 3
Output: 0
Explanation: The subarrays of nums with length 3 are:
- [4,4,4] which does not meet the requirements because the element 4 is repeated.
We return 0 because no subarrays meet the conditions.
Constraints:
1 <= k <= nums.length <= 1051 <= nums[i] <= 105
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
long long maximumSubarraySum(vector<int> &nums, int k) {
int n = int(nums.size());
auto mp = map<int, int>();
ll cur_sum = 0;
ll res = 0;
int l = 0;
for (int i = 0; i < n; i++) {
int x = nums[i];
cur_sum += x;
++mp[x];
while (mp[x] > 1 || (i - l + 1) > k) {
cur_sum -= nums[l];
--mp[nums[l]];
++l;
}
if ((i - l + 1) == k) {
res = max(res, cur_sum);
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 雇佣 K 位工人的总代价
- Difficulty: Medium
- Tag:
给你一个下标从 0 开始的整数数组 costs ,其中 costs[i] 是雇佣第 i 位工人的代价。
同时给你两个整数 k 和 candidates 。我们想根据以下规则恰好雇佣 k 位工人:
- 总共进行
k轮雇佣,且每一轮恰好雇佣一位工人。 - 在每一轮雇佣中,从最前面
candidates和最后面candidates人中选出代价最小的一位工人,如果有多位代价相同且最小的工人,选择下标更小的一位工人。- 比方说,
costs = [3,2,7,7,1,2]且candidates = 2,第一轮雇佣中,我们选择第4位工人,因为他的代价最小[3,2,7,7,1,2]。 - 第二轮雇佣,我们选择第
1位工人,因为他们的代价与第4位工人一样都是最小代价,而且下标更小,[3,2,7,7,2]。注意每一轮雇佣后,剩余工人的下标可能会发生变化。
- 比方说,
- 如果剩余员工数目不足
candidates人,那么下一轮雇佣他们中代价最小的一人,如果有多位代价相同且最小的工人,选择下标更小的一位工人。 - 一位工人只能被选择一次。
返回雇佣恰好 k 位工人的总代价。
示例 1:
输入:costs = [17,12,10,2,7,2,11,20,8], k = 3, candidates = 4
输出:11
解释:我们总共雇佣 3 位工人。总代价一开始为 0 。
- 第一轮雇佣,我们从 [17,12,10,2,7,2,11,20,8] 中选择。最小代价是 2 ,有两位工人,我们选择下标更小的一位工人,即第 3 位工人。总代价是 0 + 2 = 2 。
- 第二轮雇佣,我们从 [17,12,10,7,2,11,20,8] 中选择。最小代价是 2 ,下标为 4 ,总代价是 2 + 2 = 4 。
- 第三轮雇佣,我们从 [17,12,10,7,11,20,8] 中选择,最小代价是 7 ,下标为 3 ,总代价是 4 + 7 = 11 。注意下标为 3 的工人同时在最前面和最后面 4 位工人中。
总雇佣代价是 11 。
示例 2:
输入:costs = [1,2,4,1], k = 3, candidates = 3
输出:4
解释:我们总共雇佣 3 位工人。总代价一开始为 0 。
- 第一轮雇佣,我们从 [1,2,4,1] 中选择。最小代价为 1 ,有两位工人,我们选择下标更小的一位工人,即第 0 位工人,总代价是 0 + 1 = 1 。注意,下标为 1 和 2 的工人同时在最前面和最后面 3 位工人中。
- 第二轮雇佣,我们从 [2,4,1] 中选择。最小代价为 1 ,下标为 2 ,总代价是 1 + 1 = 2 。
- 第三轮雇佣,少于 3 位工人,我们从剩余工人 [2,4] 中选择。最小代价是 2 ,下标为 0 。总代价为 2 + 2 = 4 。
总雇佣代价是 4 。
提示:
1 <= costs.length <= 1051 <= costs[i] <= 1051 <= k, candidates <= costs.length
Metadata
- Link: Total Cost to Hire K Workers
- Difficulty: Medium
- Tag:
You are given a 0-indexed integer array costs where costs[i] is the cost of hiring the ith worker.
You are also given two integers k and candidates. We want to hire exactly k workers according to the following rules:
- You will run
ksessions and hire exactly one worker in each session. - In each hiring session, choose the worker with the lowest cost from either the first
candidatesworkers or the lastcandidatesworkers. Break the tie by the smallest index.- For example, if
costs = [3,2,7,7,1,2]andcandidates = 2, then in the first hiring session, we will choose the4thworker because they have the lowest cost[3,2,7,7,1,2]. - In the second hiring session, we will choose
1stworker because they have the same lowest cost as4thworker but they have the smallest index[3,2,7,7,2]. Please note that the indexing may be changed in the process.
- For example, if
- If there are fewer than candidates workers remaining, choose the worker with the lowest cost among them. Break the tie by the smallest index.
- A worker can only be chosen once.
Return the total cost to hire exactly k workers.
Example 1:
Input: costs = [17,12,10,2,7,2,11,20,8], k = 3, candidates = 4
Output: 11
Explanation: We hire 3 workers in total. The total cost is initially 0.
- In the first hiring round we choose the worker from [17,12,10,2,7,2,11,20,8]. The lowest cost is 2, and we break the tie by the smallest index, which is 3. The total cost = 0 + 2 = 2.
- In the second hiring round we choose the worker from [17,12,10,7,2,11,20,8]. The lowest cost is 2 (index 4). The total cost = 2 + 2 = 4.
- In the third hiring round we choose the worker from [17,12,10,7,11,20,8]. The lowest cost is 7 (index 3). The total cost = 4 + 7 = 11. Notice that the worker with index 3 was common in the first and last four workers.
The total hiring cost is 11.
Example 2:
Input: costs = [1,2,4,1], k = 3, candidates = 3
Output: 4
Explanation: We hire 3 workers in total. The total cost is initially 0.
- In the first hiring round we choose the worker from [1,2,4,1]. The lowest cost is 1, and we break the tie by the smallest index, which is 0. The total cost = 0 + 1 = 1. Notice that workers with index 1 and 2 are common in the first and last 3 workers.
- In the second hiring round we choose the worker from [2,4,1]. The lowest cost is 1 (index 2). The total cost = 1 + 1 = 2.
- In the third hiring round there are less than three candidates. We choose the worker from the remaining workers [2,4]. The lowest cost is 2 (index 0). The total cost = 2 + 2 = 4.
The total hiring cost is 4.
Constraints:
1 <= costs.length <= 1051 <= costs[i] <= 1051 <= k, candidates <= costs.length
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
long long totalCost(vector<int> &costs, int k, int candidates) {
int n = int(costs.size());
auto se = set<pair<int, int>>();
auto vis = vector<int>(n + 1, 0);
const auto add = [&vis, &se, &costs, &n](int x) {
if (x < 0 || x >= n) {
return;
}
if (vis[x] == 1) {
return;
}
vis[x] = 1;
se.insert(make_pair(costs[x], x));
};
int l = candidates - 1;
int r = n - candidates;
for (int i = 0; i <= l; i++) {
add(i);
}
for (int i = r; i < n; i++) {
add(i);
}
ll res = 0;
for (int cnt = 0; cnt < k; cnt++) {
auto pos = se.begin();
res += pos->first;
int pp = pos->second;
se.erase(pos);
if (pp <= l) {
++l;
add(l);
} else {
--r;
add(r);
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 最小移动总距离
- Difficulty: Hard
- Tag:
X 轴上有一些机器人和工厂。给你一个整数数组 robot ,其中 robot[i] 是第 i 个机器人的位置。再给你一个二维整数数组 factory ,其中 factory[j] = [positionj, limitj] ,表示第 j 个工厂的位置在 positionj ,且第 j 个工厂最多可以修理 limitj 个机器人。
每个机器人所在的位置 互不相同 。每个工厂所在的位置也 互不相同 。注意一个机器人可能一开始跟一个工厂在 相同的位置 。
所有机器人一开始都是坏的,他们会沿着设定的方向一直移动。设定的方向要么是 X 轴的正方向,要么是 X 轴的负方向。当一个机器人经过一个没达到上限的工厂时,这个工厂会维修这个机器人,且机器人停止移动。
任何时刻,你都可以设置 部分 机器人的移动方向。你的目标是最小化所有机器人总的移动距离。
请你返回所有机器人移动的最小总距离。测试数据保证所有机器人都可以被维修。
注意:
- 所有机器人移动速度相同。
- 如果两个机器人移动方向相同,它们永远不会碰撞。
- 如果两个机器人迎面相遇,它们也不会碰撞,它们彼此之间会擦肩而过。
- 如果一个机器人经过了一个已经达到上限的工厂,机器人会当作工厂不存在,继续移动。
- 机器人从位置
x到位置y的移动距离为|y - x|。
示例 1:
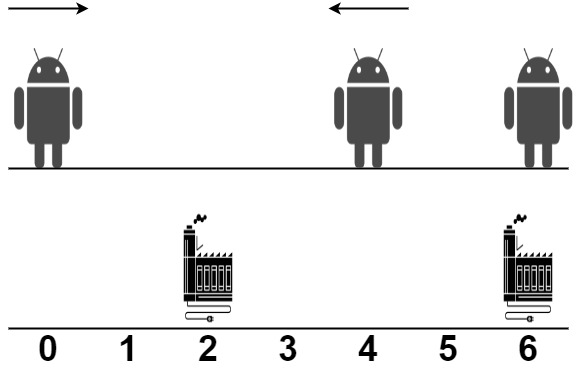
输入:robot = [0,4,6], factory = [[2,2],[6,2]]
输出:4
解释:如上图所示:
- 第一个机器人从位置 0 沿着正方向移动,在第一个工厂处维修。
- 第二个机器人从位置 4 沿着负方向移动,在第一个工厂处维修。
- 第三个机器人在位置 6 被第二个工厂维修,它不需要移动。
第一个工厂的维修上限是 2 ,它维修了 2 个机器人。
第二个工厂的维修上限是 2 ,它维修了 1 个机器人。
总移动距离是 |2 - 0| + |2 - 4| + |6 - 6| = 4 。没有办法得到比 4 更少的总移动距离。
示例 2:

输入:robot = [1,-1], factory = [[-2,1],[2,1]]
输出:2
解释:如上图所示:
- 第一个机器人从位置 1 沿着正方向移动,在第二个工厂处维修。
- 第二个机器人在位置 -1 沿着负方向移动,在第一个工厂处维修。
第一个工厂的维修上限是 1 ,它维修了 1 个机器人。
第二个工厂的维修上限是 1 ,它维修了 1 个机器人。
总移动距离是 |2 - 1| + |(-2) - (-1)| = 2 。没有办法得到比 2 更少的总移动距离。
提示:
1 <= robot.length, factory.length <= 100factory[j].length == 2-109 <= robot[i], positionj <= 1090 <= limitj <= robot.length- 测试数据保证所有机器人都可以被维修。
Metadata
- Link: Minimum Total Distance Traveled
- Difficulty: Hard
- Tag:
There are some robots and factories on the X-axis. You are given an integer array robot where robot[i] is the position of the ith robot. You are also given a 2D integer array factory where factory[j] = [positionj, limitj] indicates that positionj is the position of the jth factory and that the jth factory can repair at most limitj robots.
The positions of each robot are unique. The positions of each factory are also unique. Note that a robot can be in the same position as a factory initially.
All the robots are initially broken; they keep moving in one direction. The direction could be the negative or the positive direction of the X-axis. When a robot reaches a factory that did not reach its limit, the factory repairs the robot, and it stops moving.
At any moment, you can set the initial direction of moving for some robot. Your target is to minimize the total distance traveled by all the robots.
Return the minimum total distance traveled by all the robots. The test cases are generated such that all the robots can be repaired.
Note that
- All robots move at the same speed.
- If two robots move in the same direction, they will never collide.
- If two robots move in opposite directions and they meet at some point, they do not collide. They cross each other.
- If a robot passes by a factory that reached its limits, it crosses it as if it does not exist.
- If the robot moved from a position
xto a positiony, the distance it moved is|y - x|.
Example 1:
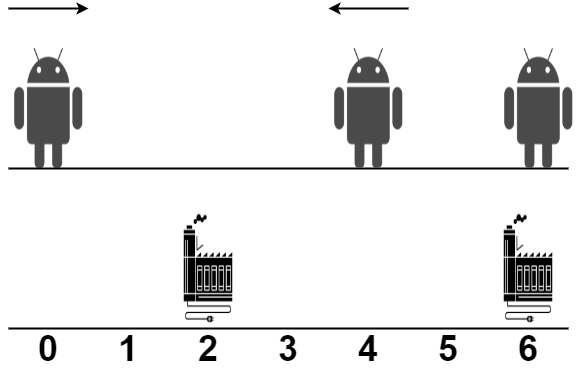
Input: robot = [0,4,6], factory = [[2,2],[6,2]]
Output: 4
Explanation: As shown in the figure:
- The first robot at position 0 moves in the positive direction. It will be repaired at the first factory.
- The second robot at position 4 moves in the negative direction. It will be repaired at the first factory.
- The third robot at position 6 will be repaired at the second factory. It does not need to move.
The limit of the first factory is 2, and it fixed 2 robots.
The limit of the second factory is 2, and it fixed 1 robot.
The total distance is |2 - 0| + |2 - 4| + |6 - 6| = 4. It can be shown that we cannot achieve a better total distance than 4.
Example 2:
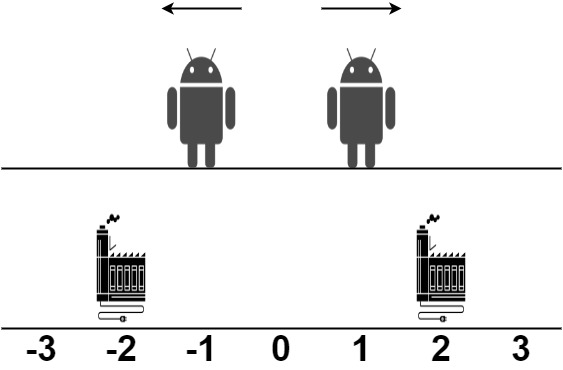
Input: robot = [1,-1], factory = [[-2,1],[2,1]]
Output: 2
Explanation: As shown in the figure:
- The first robot at position 1 moves in the positive direction. It will be repaired at the second factory.
- The second robot at position -1 moves in the negative direction. It will be repaired at the first factory.
The limit of the first factory is 1, and it fixed 1 robot.
The limit of the second factory is 1, and it fixed 1 robot.
The total distance is |2 - 1| + |(-2) - (-1)| = 2. It can be shown that we cannot achieve a better total distance than 2.
Constraints:
1 <= robot.length, factory.length <= 100factory[j].length == 2-109 <= robot[i], positionj <= 1090 <= limitj <= robot.length- The input will be generated such that it is always possible to repair every robot.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
const ll INF = 0x3f3f3f3f;
const int N = 4e3 + 10;
struct edge {
int to, capacity, cost, rev;
edge() {}
edge(int to, int _capacity, int _cost, int _rev) : to(to), capacity(_capacity), cost(_cost), rev(_rev) {}
};
struct Min_Cost_Max_Flow {
int V;
ll H[N + 5], dis[N + 5], PreV[N + 5], PreE[N + 5];
vector<edge> G[N + 5];
void Init(int n) {
V = n;
for (int i = 0; i <= V; ++i) G[i].clear();
}
void addedge(int from, int to, int cap, int cost) {
G[from].push_back(edge(to, cap, cost, G[to].size()));
G[to].push_back(edge(from, 0, -cost, G[from].size() - 1));
}
ll Min_cost_max_flow(int s, int t, ll f, int &flow) {
ll res = 0;
fill(H, H + 1 + V, 0);
while (f) {
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
fill(dis, dis + 1 + V, INF);
dis[s] = 0;
q.push(pair<int, int>(0, s));
while (!q.empty()) {
pair<int, int> now = q.top();
q.pop();
int v = now.second;
if (dis[v] < now.first)
continue;
for (int i = 0, sze = (int)G[v].size(); i < sze; ++i) {
edge &e = G[v][i];
if (e.capacity > 0 && dis[e.to] > dis[v] + e.cost + H[v] - H[e.to]) {
dis[e.to] = dis[v] + e.cost + H[v] - H[e.to];
PreV[e.to] = v;
PreE[e.to] = i;
q.push(pair<int, int>(dis[e.to], e.to));
}
}
}
if (dis[t] == INF)
break;
for (int i = 0; i <= V; ++i) H[i] += dis[i];
int d = f;
for (int v = t; v != s; v = PreV[v]) d = min(d, G[PreV[v]][PreE[v]].capacity);
f -= d;
flow += d;
res += d * H[t];
for (int v = t; v != s; v = PreV[v]) {
edge &e = G[PreV[v]][PreE[v]];
e.capacity -= d;
G[v][e.rev].capacity += d;
}
}
return res;
}
} MCMF;
class Solution {
public:
long long minimumTotalDistance(vector<int> &robot, vector<vector<int>> &factory) {
int n = int(robot.size());
int m = int(factory.size());
int t = n + m + 10;
MCMF.Init(t);
int st = 0;
int ed = t;
for (int i = 1; i <= n; i++) {
MCMF.addedge(st, i, 1, 0);
}
for (int j = 1; j <= m; j++) {
MCMF.addedge(n + j, ed, factory[j - 1][1], 0);
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
MCMF.addedge(i, n + j, 1, abs(robot[i - 1] - factory[j - 1][0]));
}
}
int flow = 0;
ll res = MCMF.Min_cost_max_flow(st, ed, INF, flow);
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif