跳转至

weekly-contest-292

A

Statement

Metadata

给你一个字符串 num ，表示一个大整数。如果一个整数满足下述所有条件，则认为该整数是一个 优质整数 ：

  • 该整数是 num 的一个长度为 3 的 子字符串 。
  • 该整数由唯一一个数字重复 3 次组成。

以字符串形式返回 最大的优质整数 。如果不存在满足要求的整数，则返回一个空字符串 "" 。

注意：

  • 子字符串 是字符串中的一个连续字符序列。
  • num 或优质整数中可能存在 前导零 。

 

示例 1：

输入：num = "6777133339"
输出："777"
解释：num 中存在两个优质整数："777" 和 "333" 。
"777" 是最大的那个，所以返回 "777" 。

示例 2：

输入：num = "2300019"
输出："000"
解释："000" 是唯一一个优质整数。

示例 3：

输入：num = "42352338"
输出：""
解释：不存在长度为 3 且仅由一个唯一数字组成的整数。因此，不存在优质整数。

 

提示：

  • 3 <= num.length <= 1000
  • num 仅由数字（0 - 9）组成

Metadata

You are given a string num representing a large integer. An integer is good if it meets the following conditions:

  • It is a substring of num with length 3.
  • It consists of only one unique digit.

Return the maximum good integer as a string or an empty string "" if no such integer exists.

Note:

  • A substring is a contiguous sequence of characters within a string.
  • There may be leading zeroes in num or a good integer.

 

Example 1:

Input: num = "6777133339"
Output: "777"
Explanation: There are two distinct good integers: "777" and "333".
"777" is the largest, so we return "777".

Example 2:

Input: num = "2300019"
Output: "000"
Explanation: "000" is the only good integer.

Example 3:

Input: num = "42352338"
Output: ""
Explanation: No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.

 

Constraints:

  • 3 <= num.length <= 1000
  • num only consists of digits.

Solution

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <string>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    string largestGoodInteger(string s) {
        string res = "";
        int m = -1;
        int n = static_cast<int>(s.size());
        for (int i = 2; i < n; i++) {
            string t = s.substr(i - 2, 3);
            if (t[0] == t[1] && t[1] == t[2]) {
                int cur = 0;
                for (int j = 0; j < 3; j++) {
                    cur = cur * 10 + (t[j] - '0');
                }

                if (cur > m) {
                    m = cur;
                    res = t;
                }
            }
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

Metadata

给你一棵二叉树的根节点 root ，找出并返回满足要求的节点数，要求节点的值等于其 子树 中值的 平均值 。

注意：

  • n 个元素的平均值可以由 n 个元素 求和 然后再除以 n ，并 向下舍入 到最近的整数。
  • root 的 子树 由 root 和它的所有后代组成。

 

示例 1：

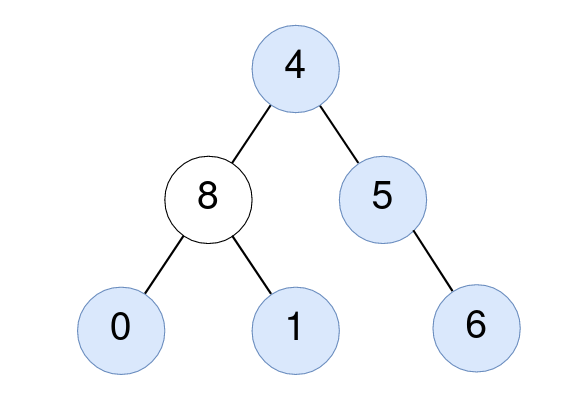
输入：root = [4,8,5,0,1,null,6]
输出：5
解释：
对值为 4 的节点：子树的平均值 (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4 。
对值为 5 的节点：子树的平均值 (5 + 6) / 2 = 11 / 2 = 5 。
对值为 0 的节点：子树的平均值 0 / 1 = 0 。
对值为 1 的节点：子树的平均值 1 / 1 = 1 。
对值为 6 的节点：子树的平均值 6 / 1 = 6 。

示例 2：

输入：root = [1]
输出：1
解释：对值为 1 的节点：子树的平均值 1 / 1 = 1。

 

提示：

  • 树中节点数目在范围 [1, 1000] 内
  • 0 <= Node.val <= 1000

Metadata

Given the root of a binary tree, return the number of nodes where the value of the node is equal to the average of the values in its subtree.

Note:

  • The average of n elements is the sum of the n elements divided by n and rounded down to the nearest integer.
  • A subtree of root is a tree consisting of root and all of its descendants.

 

Example 1:

Input: root = [4,8,5,0,1,null,6]
Output: 5
Explanation: 
For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4.
For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5.
For the node with value 0: The average of its subtree is 0 / 1 = 0.
For the node with value 1: The average of its subtree is 1 / 1 = 1.
For the node with value 6: The average of its subtree is 6 / 1 = 6.

Example 2:

Input: root = [1]
Output: 1
Explanation: For the node with value 1: The average of its subtree is 1 / 1 = 1.

 

Constraints:

  • The number of nodes in the tree is in the range [1, 1000].
  • 0 <= Node.val <= 1000

Solution

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <utility>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

#ifdef LOCAL

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

#endif

class Solution {
public:
    int res;

    std::pair<int, int> dfs(TreeNode *rt) {
        if (!rt) {
            return make_pair(0, 0);
        }

        int sum = 0;
        int sze = 0;

        {
            const auto &[a, b] = dfs(rt->left);
            sum += a;
            sze += b;
        }

        {
            const auto &[a, b] = dfs(rt->right);
            sum += a;
            sze += b;
        }

        sum += rt->val;
        ++sze;

        if (sum / sze == rt->val) {
            ++res;
        }

        return make_pair(sum, sze);
    }

    int averageOfSubtree(TreeNode *root) {
        res = 0;
        dfs(root);
        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

Metadata

Alice 在给 Bob 用手机打字。数字到字母的 对应 如下图所示。

为了 打出 一个字母，Alice 需要 按 对应字母 i 次，i 是该字母在这个按键上所处的位置。

  • 比方说，为了按出字母 's' ，Alice 需要按 '7' 四次。类似的， Alice 需要按 '5' 两次得到字母  'k' 。
  • 注意，数字 '0' 和 '1' 不映射到任何字母，所以 Alice 不 使用它们。

但是，由于传输的错误，Bob 没有收到 Alice 打字的字母信息，反而收到了 按键的字符串信息 。

  • 比方说，Alice 发出的信息为 "bob" ，Bob 将收到字符串 "2266622" 。

给你一个字符串 pressedKeys ，表示 Bob 收到的字符串，请你返回 Alice 总共可能发出多少种文字信息 。

由于答案可能很大，将它对 109 + 7 取余 后返回。

 

示例 1：

输入：pressedKeys = "22233"
输出：8
解释：
Alice 可能发出的文字信息包括：
"aaadd", "abdd", "badd", "cdd", "aaae", "abe", "bae" 和 "ce" 。
由于总共有 8 种可能的信息，所以我们返回 8 。

示例 2：

输入：pressedKeys = "222222222222222222222222222222222222"
输出：82876089
解释：
总共有 2082876103 种 Alice 可能发出的文字信息。
由于我们需要将答案对 109 + 7 取余，所以我们返回 2082876103 % (109 + 7) = 82876089 。

 

提示：

  • 1 <= pressedKeys.length <= 105
  • pressedKeys 只包含数字 '2' 到 '9' 。

Metadata

Alice is texting Bob using her phone. The mapping of digits to letters is shown in the figure below.

In order to add a letter, Alice has to press the key of the corresponding digit i times, where i is the position of the letter in the key.

  • For example, to add the letter 's', Alice has to press '7' four times. Similarly, to add the letter 'k', Alice has to press '5' twice.
  • Note that the digits '0' and '1' do not map to any letters, so Alice does not use them.

However, due to an error in transmission, Bob did not receive Alice's text message but received a string of pressed keys instead.

  • For example, when Alice sent the message "bob", Bob received the string "2266622".

Given a string pressedKeys representing the string received by Bob, return the total number of possible text messages Alice could have sent.

Since the answer may be very large, return it modulo 109 + 7.

 

Example 1:

Input: pressedKeys = "22233"
Output: 8
Explanation:
The possible text messages Alice could have sent are:
"aaadd", "abdd", "badd", "cdd", "aaae", "abe", "bae", and "ce".
Since there are 8 possible messages, we return 8.

Example 2:

Input: pressedKeys = "222222222222222222222222222222222222"
Output: 82876089
Explanation:
There are 2082876103 possible text messages Alice could have sent.
Since we need to return the answer modulo 109 + 7, we return 2082876103 % (109 + 7) = 82876089.

 

Constraints:

  • 1 <= pressedKeys.length <= 105
  • pressedKeys only consists of digits from '2' - '9'.

Solution

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

const int mod = 1e9 + 7;
const int N = 1e5 + 10;
int f[N], g[N];

class Solution {
public:
    void init() {
        if (f[0] == 1) {
            return;
        }

        f[0] = 1;

        for (int i = 1; i <= 1e5; i++) {
            for (int j = 1; j <= 3; j++) {
                if (i - j >= 0) {
                    f[i] += f[i - j];
                    if (f[i] >= mod) {
                        f[i] -= mod;
                    }
                }
            }
        }

        g[0] = 1;

        for (int i = 1; i <= 1e5; i++) {
            for (int j = 1; j <= 4; j++) {
                if (i - j >= 0) {
                    g[i] += g[i - j];
                    if (g[i] >= mod) {
                        g[i] -= mod;
                    }
                }
            }
        }
    }

    int countTexts(string s) {
        init();

        int res = 1;
        int n = static_cast<int>(s.size());

        int pre = -1;
        int cnt = 0;
        for (int i = 0; i < n; i++) {
            if (s[i] == pre) {
                ++cnt;
            } else {
                if (pre == '7' || pre == '9') {
                    res = 1ll * res * g[cnt] % mod;
                } else {
                    res = 1ll * res * f[cnt] % mod;
                }

                pre = s[i];
                cnt = 1;
            }
        }

        if (pre == '7' || pre == '9') {
            res = 1ll * res * g[cnt] % mod;
        } else {
            res = 1ll * res * f[cnt] % mod;
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

D

Statement

Metadata

一个括号字符串是一个 非空 且只包含 '(' 和 ')' 的字符串。如果下面 任意 条件为 真 ，那么这个括号字符串就是 合法的 。

  • 字符串是 () 。
  • 字符串可以表示为 AB（A 连接 B），A 和 B 都是合法括号序列。
  • 字符串可以表示为 (A) ，其中 A 是合法括号序列。

给你一个 m x n 的括号网格图矩阵 grid 。网格图中一个 合法括号路径 是满足以下所有条件的一条路径：

  • 路径开始于左上角格子 (0, 0) 。
  • 路径结束于右下角格子 (m - 1, n - 1) 。
  • 路径每次只会向 下 或者向 右 移动。
  • 路径经过的格子组成的括号字符串是 合法 的。

如果网格图中存在一条 合法括号路径 ，请返回 true ，否则返回 false 。

 

示例 1：

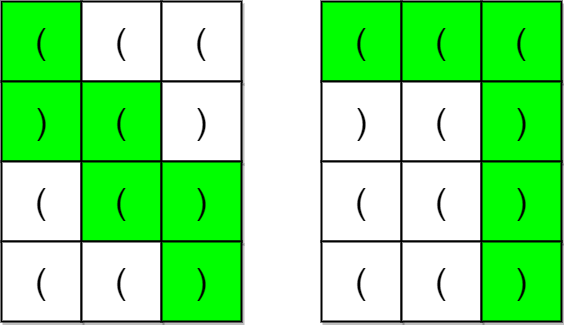
输入：grid = [["(","(","("],[")","(",")"],["(","(",")"],["(","(",")"]]
输出：true
解释：上图展示了两条路径，它们都是合法括号字符串路径。
第一条路径得到的合法字符串是 "()(())" 。
第二条路径得到的合法字符串是 "((()))" 。
注意可能有其他的合法括号字符串路径。

示例 2：

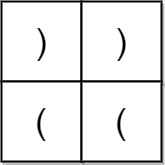
输入：grid = [[")",")"],["(","("]]
输出：false
解释：两条可行路径分别得到 "))(" 和 ")((" 。由于它们都不是合法括号字符串，我们返回 false 。

 

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 100
  • grid[i][j] 要么是 '(' ，要么是 ')' 。

Metadata

A parentheses string is a non-empty string consisting only of '(' and ')'. It is valid if any of the following conditions is true:

  • It is ().
  • It can be written as AB (A concatenated with B), where A and B are valid parentheses strings.
  • It can be written as (A), where A is a valid parentheses string.

You are given an m x n matrix of parentheses grid. A valid parentheses string path in the grid is a path satisfying all of the following conditions:

  • The path starts from the upper left cell (0, 0).
  • The path ends at the bottom-right cell (m - 1, n - 1).
  • The path only ever moves down or right.
  • The resulting parentheses string formed by the path is valid.

Return true if there exists a valid parentheses string path in the grid. Otherwise, return false.

 

Example 1:

Input: grid = [["(","(","("],[")","(",")"],["(","(",")"],["(","(",")"]]
Output: true
Explanation: The above diagram shows two possible paths that form valid parentheses strings.
The first path shown results in the valid parentheses string "()(())".
The second path shown results in the valid parentheses string "((()))".
Note that there may be other valid parentheses string paths.

Example 2:

Input: grid = [[")",")"],["(","("]]
Output: false
Explanation: The two possible paths form the parentheses strings "))(" and ")((". Since neither of them are valid parentheses strings, we return false.

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 100
  • grid[i][j] is either '(' or ')'.

Solution

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <stack>
#include <vector>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

int mv[][2] = {
        {0, 1},
        {1, 0},
};

struct node {
    int x, y, c;
};

class Solution {
public:
    vector<vector<char>> g;
    bool bfs() {
        int n = static_cast<int>(g.size());
        int m = static_cast<int>(g[0].size());

        const auto ok = [&](int x, int y) -> bool {
            if (x < 0 || x >= n || y < 0 || y >= m) {
                return false;
            }

            return true;
        };

        auto f = vector<vector<vector<int>>>(n + 1, vector<vector<int>>(m + 1, vector<int>(210, 0)));

        if (g[0][0] == ')') {
            return false;
        }

        if (g[n - 1][m - 1] == '(') {
            return false;
        }

        queue<node> q;

        q.push({
                .x = 0,
                .y = 0,
                .c = 1,
        });

        f[0][0][1] = 1;

        while (!q.empty()) {
            auto t = q.front();
            q.pop();

            int x = t.x;
            int y = t.y;
            int c = t.c;

            for (int i = 0; i < 2; i++) {
                int nx = x + mv[i][0];
                int ny = y + mv[i][1];
                int cc = c;

                if (ok(nx, ny)) {
                    if (g[nx][ny] == '(') {
                        ++cc;
                    } else {
                        --cc;
                    }

                    if (cc < 0) {
                        continue;
                    }

                    if (f[nx][ny][cc]) {
                        continue;
                    }

                    f[nx][ny][cc] = 1;
                    q.push({
                            .x = nx,
                            .y = ny,
                            .c = cc,
                    });
                }
            }
        }

        return f[n - 1][m - 1][0];
    }

    bool hasValidPath(vector<vector<char>> &grid) {
        g = vector<vector<char>>(grid);

        return bfs();
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif
最后更新: October 11, 2023
回到页面顶部