weekly-contest-323
A
Statement
Metadata
- Link: 删除每行中的最大值
- Difficulty: Easy
- Tag:
给你一个 m x n 大小的矩阵 grid ,由若干正整数组成。
执行下述操作,直到 grid 变为空矩阵:
- 从每一行删除值最大的元素。如果存在多个这样的值,删除其中任何一个。
- 将删除元素中的最大值与答案相加。
注意 每执行一次操作,矩阵中列的数据就会减 1 。
返回执行上述操作后的答案。
示例 1:
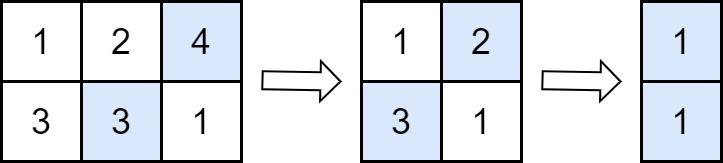
输入:grid = [[1,2,4],[3,3,1]]
输出:8
解释:上图展示在每一步中需要移除的值。
- 在第一步操作中,从第一行删除 4 ,从第二行删除 3(注意,有两个单元格中的值为 3 ,我们可以删除任一)。在答案上加 4 。
- 在第二步操作中,从第一行删除 2 ,从第二行删除 3 。在答案上加 3 。
- 在第三步操作中,从第一行删除 1 ,从第二行删除 1 。在答案上加 1 。
最终,答案 = 4 + 3 + 1 = 8 。
示例 2:

输入:grid = [[10]]
输出:10
解释:上图展示在每一步中需要移除的值。
- 在第一步操作中,从第一行删除 10 。在答案上加 10 。
最终,答案 = 10 。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 501 <= grid[i][j] <= 100
Metadata
- Link: Delete Greatest Value in Each Row
- Difficulty: Easy
- Tag:
You are given an m x n matrix grid consisting of positive integers.
Perform the following operation until grid becomes empty:
- Delete the element with the greatest value from each row. If multiple such elements exist, delete any of them.
- Add the maximum of deleted elements to the answer.
Note that the number of columns decreases by one after each operation.
Return the answer after performing the operations described above.
Example 1:

Input: grid = [[1,2,4],[3,3,1]]
Output: 8
Explanation: The diagram above shows the removed values in each step.
- In the first operation, we remove 4 from the first row and 3 from the second row (notice that, there are two cells with value 3 and we can remove any of them). We add 4 to the answer.
- In the second operation, we remove 2 from the first row and 3 from the second row. We add 3 to the answer.
- In the third operation, we remove 1 from the first row and 1 from the second row. We add 1 to the answer.
The final answer = 4 + 3 + 1 = 8.
Example 2:

Input: grid = [[10]]
Output: 10
Explanation: The diagram above shows the removed values in each step.
- In the first operation, we remove 10 from the first row. We add 10 to the answer.
The final answer = 10.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 501 <= grid[i][j] <= 100
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int deleteGreatestValue(vector<vector<int>> &grid) {
int n = int(grid.size());
int m = int(grid[0].size());
int ans = 0;
for (int i = 0; i < n; i++) {
sort(all(grid[i]));
}
for (int j = 0; j < m; j++) {
int mx = 0;
for (int i = 0; i < n; i++) {
mx = max(mx, grid[i][j]);
}
ans += mx;
}
return ans;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 数组中最长的方波
- Difficulty: Medium
- Tag:
给你一个整数数组 nums 。如果 nums 的子序列满足下述条件,则认为该子序列是一个 方波 :
- 子序列的长度至少为
2,并且 - 将子序列从小到大排序 之后 ,除第一个元素外,每个元素都是前一个元素的 平方 。
返回 nums 中 最长方波 的长度,如果不存在 方波 则返回 -1 。
子序列 也是一个数组,可以由另一个数组删除一些或不删除元素且不改变剩余元素的顺序得到。
示例 1 :
输入:nums = [4,3,6,16,8,2]
输出:3
解释:选出子序列 [4,16,2] 。排序后,得到 [2,4,16] 。
- 4 = 2 * 2.
- 16 = 4 * 4.
因此,[4,16,2] 是一个方波.
可以证明长度为 4 的子序列都不是方波。
示例 2 :
输入:nums = [2,3,5,6,7]
输出:-1
解释:nums 不存在方波,所以返回 -1 。
提示:
2 <= nums.length <= 1052 <= nums[i] <= 105
Metadata
- Link: Longest Square Streak in an Array
- Difficulty: Medium
- Tag:
You are given an integer array nums. A subsequence of nums is called a square streak if:
- The length of the subsequence is at least
2, and - after sorting the subsequence, each element (except the first element) is the square of the previous number.
Return the length of the longest square streak in nums, or return -1 if there is no square streak.
A subsequence is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
Example 1:
Input: nums = [4,3,6,16,8,2]
Output: 3
Explanation: Choose the subsequence [4,16,2]. After sorting it, it becomes [2,4,16].
- 4 = 2 * 2.
- 16 = 4 * 4.
Therefore, [4,16,2] is a square streak.
It can be shown that every subsequence of length 4 is not a square streak.
Example 2:
Input: nums = [2,3,5,6,7]
Output: -1
Explanation: There is no square streak in nums so return -1.
Constraints:
2 <= nums.length <= 1052 <= nums[i] <= 105
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int longestSquareStreak(vector<int> &nums) {
sort(all(nums));
auto mp = map<int, int>();
for (const auto &a : nums) {
int x = int(sqrt(a));
if (x * x == a) {
mp[a] = mp[x] + 1;
} else {
mp[a] = 1;
}
}
int res = 0;
for (const auto &[k, v] : mp) {
res = max(res, v);
}
return res == 1 ? -1 : res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 设计内存分配器
- Difficulty: Medium
- Tag:
给你一个整数 n ,表示下标从 0 开始的内存数组的大小。所有内存单元开始都是空闲的。
请你设计一个具备以下功能的内存分配器:
- 分配 一块大小为
size的连续空闲内存单元并赋 idmID。 - 释放 给定 id
mID对应的所有内存单元。
注意:
- 多个块可以被分配到同一个
mID。 - 你必须释放
mID对应的所有内存单元,即便这些内存单元被分配在不同的块中。
实现 Allocator 类:
Allocator(int n)使用一个大小为n的内存数组初始化Allocator对象。int allocate(int size, int mID)找出大小为size个连续空闲内存单元且位于 最左侧 的块,分配并赋 idmID。返回块的第一个下标。如果不存在这样的块,返回-1。int free(int mID)释放 idmID对应的所有内存单元。返回释放的内存单元数目。
示例:
输入
["Allocator", "allocate", "allocate", "allocate", "free", "allocate", "allocate", "allocate", "free", "allocate", "free"]
[[10], [1, 1], [1, 2], [1, 3], [2], [3, 4], [1, 1], [1, 1], [1], [10, 2], [7]]
输出
[null, 0, 1, 2, 1, 3, 1, 6, 3, -1, 0]
解释
Allocator loc = new Allocator(10); // 初始化一个大小为 10 的内存数组,所有内存单元都是空闲的。
loc.allocate(1, 1); // 最左侧的块的第一个下标是 0 。内存数组变为 [1, , , , , , , , , ]。返回 0 。
loc.allocate(1, 2); // 最左侧的块的第一个下标是 1 。内存数组变为 [1,2, , , , , , , , ]。返回 1 。
loc.allocate(1, 3); // 最左侧的块的第一个下标是 2 。内存数组变为 [1,2,3, , , , , , , ]。返回 2 。
loc.free(2); // 释放 mID 为 2 的所有内存单元。内存数组变为 [1, ,3, , , , , , , ] 。返回 1 ,因为只有 1 个 mID 为 2 的内存单元。
loc.allocate(3, 4); // 最左侧的块的第一个下标是 3 。内存数组变为 [1, ,3,4,4,4, , , , ]。返回 3 。
loc.allocate(1, 1); // 最左侧的块的第一个下标是 1 。内存数组变为 [1,1,3,4,4,4, , , , ]。返回 1 。
loc.allocate(1, 1); // 最左侧的块的第一个下标是 6 。内存数组变为 [1,1,3,4,4,4,1, , , ]。返回 6 。
loc.free(1); // 释放 mID 为 1 的所有内存单元。内存数组变为 [ , ,3,4,4,4, , , , ] 。返回 3 ,因为有 3 个 mID 为 1 的内存单元。
loc.allocate(10, 2); // 无法找出长度为 10 个连续空闲内存单元的空闲块,所有返回 -1 。
loc.free(7); // 释放 mID 为 7 的所有内存单元。内存数组保持原状,因为不存在 mID 为 7 的内存单元。返回 0 。
提示:
1 <= n, size, mID <= 1000- 最多调用
allocate和free方法1000次
Metadata
- Link: Design Memory Allocator
- Difficulty: Medium
- Tag:
You are given an integer n representing the size of a 0-indexed memory array. All memory units are initially free.
You have a memory allocator with the following functionalities:
- Allocate a block of
sizeconsecutive free memory units and assign it the idmID. - Free all memory units with the given id
mID.
Note that:
- Multiple blocks can be allocated to the same
mID. - You should free all the memory units with
mID, even if they were allocated in different blocks.
Implement the Allocator class:
Allocator(int n)Initializes anAllocatorobject with a memory array of sizen.int allocate(int size, int mID)Find the leftmost block ofsizeconsecutive free memory units and allocate it with the idmID. Return the block's first index. If such a block does not exist, return-1.int free(int mID)Free all memory units with the idmID. Return the number of memory units you have freed.
Example 1:
Input
["Allocator", "allocate", "allocate", "allocate", "free", "allocate", "allocate", "allocate", "free", "allocate", "free"]
[[10], [1, 1], [1, 2], [1, 3], [2], [3, 4], [1, 1], [1, 1], [1], [10, 2], [7]]
Output
[null, 0, 1, 2, 1, 3, 1, 6, 3, -1, 0]
Explanation
Allocator loc = new Allocator(10); // Initialize a memory array of size 10. All memory units are initially free.
loc.allocate(1, 1); // The leftmost block's first index is 0. The memory array becomes [1,,,,,,,,,]. We return 0.
loc.allocate(1, 2); // The leftmost block's first index is 1. The memory array becomes [1,2,,,,,,,,]. We return 1.
loc.allocate(1, 3); // The leftmost block's first index is 2. The memory array becomes [1,2,3,,,,,,,]. We return 2.
loc.free(2); // Free all memory units with mID 2. The memory array becomes [1,, 3,,,,,,,]. We return 1 since there is only 1 unit with mID 2.
loc.allocate(3, 4); // The leftmost block's first index is 3. The memory array becomes [1,,3,4,4,4,,,,]. We return 3.
loc.allocate(1, 1); // The leftmost block's first index is 1. The memory array becomes [1,1,3,4,4,4,,,,]. We return 1.
loc.allocate(1, 1); // The leftmost block's first index is 6. The memory array becomes [1,1,3,4,4,4,1,,,]. We return 6.
loc.free(1); // Free all memory units with mID 1. The memory array becomes [,,3,4,4,4,,,,]. We return 3 since there are 3 units with mID 1.
loc.allocate(10, 2); // We can not find any free block with 10 consecutive free memory units, so we return -1.
loc.free(7); // Free all memory units with mID 7. The memory array remains the same since there is no memory unit with mID 7. We return 0.
Constraints:
1 <= n, size, mID <= 1000- At most
1000calls will be made toallocateandfree.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Allocator {
public:
vector<int> mem;
int n;
Allocator(int n) {
this->n = n;
mem = vector<int>(n + 5, 0);
}
int allocate(int size, int mID) {
for (int i = 0; i < n && i + size <= n; i++) {
if (mem[i] != 0) {
continue;
}
int ok = 1;
for (int j = i; j - i < size; j++) {
if (mem[j] != 0) {
i = j;
ok = 0;
break;
}
}
if (ok) {
for (int j = i; j - i < size; j++) {
mem[j] = mID;
}
return i;
}
}
return -1;
}
int free(int mID) {
int cnt = 0;
for (int i = 0; i < n; i++) {
if (mem[i] == mID) {
mem[i] = 0;
++cnt;
}
}
return cnt;
}
};
/**
* Your Allocator object will be instantiated and called as such:
* Allocator* obj = new Allocator(n);
* int param_1 = obj->allocate(size,mID);
* int param_2 = obj->free(mID);
*/
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 矩阵查询可获得的最大分数
- Difficulty: Hard
- Tag:
给你一个大小为 m x n 的整数矩阵 grid 和一个大小为 k 的数组 queries 。
找出一个大小为 k 的数组 answer ,且满足对于每个整数 queres[i] ,你从矩阵 左上角 单元格开始,重复以下过程:
- 如果
queries[i]严格 大于你当前所处位置单元格,如果该单元格是第一次访问,则获得 1 分,并且你可以移动到所有4个方向(上、下、左、右)上任一 相邻 单元格。 - 否则,你不能获得任何分,并且结束这一过程。
在过程结束后,answer[i] 是你可以获得的最大分数。注意,对于每个查询,你可以访问同一个单元格 多次 。
返回结果数组 answer 。
示例 1:
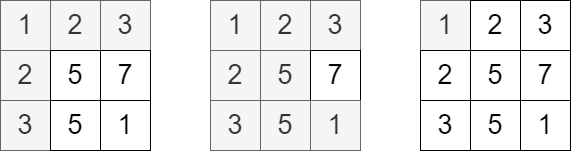
输入:grid = [[1,2,3],[2,5,7],[3,5,1]], queries = [5,6,2]
输出:[5,8,1]
解释:上图展示了每个查询中访问并获得分数的单元格。示例 2:
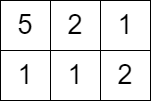
输入:grid = [[5,2,1],[1,1,2]], queries = [3]
输出:[0]
解释:无法获得分数,因为左上角单元格的值大于等于 3 。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 10004 <= m * n <= 105k == queries.length1 <= k <= 1041 <= grid[i][j], queries[i] <= 106
Metadata
- Link: Maximum Number of Points From Grid Queries
- Difficulty: Hard
- Tag:
You are given an m x n integer matrix grid and an array queries of size k.
Find an array answer of size k such that for each integer queres[i] you start in the top left cell of the matrix and repeat the following process:
- If
queries[i]is strictly greater than the value of the current cell that you are in, then you get one point if it is your first time visiting this cell, and you can move to any adjacent cell in all4directions: up, down, left, and right. - Otherwise, you do not get any points, and you end this process.
After the process, answer[i] is the maximum number of points you can get. Note that for each query you are allowed to visit the same cell multiple times.
Return the resulting array answer.
Example 1:

Input: grid = [[1,2,3],[2,5,7],[3,5,1]], queries = [5,6,2]
Output: [5,8,1]
Explanation: The diagrams above show which cells we visit to get points for each query.Example 2:

Input: grid = [[5,2,1],[1,1,2]], queries = [3]
Output: [0]
Explanation: We can not get any points because the value of the top left cell is already greater than or equal to 3.
Constraints:
m == grid.lengthn == grid[i].length2 <= m, n <= 10004 <= m * n <= 105k == queries.length1 <= k <= 1041 <= grid[i][j], queries[i] <= 106
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
struct QNode {
int ix;
int v;
};
const int N = 1e5 + 10;
struct UFS {
int fa[N], sze[N];
void init(int n) {
memset(fa, -1, sizeof(fa[0]) * (n + 5));
for (int i = 0; i <= n; i++) {
sze[i] = 1;
}
}
int find(int x) {
return fa[x] == -1 ? x : fa[x] = find(fa[x]);
}
bool merge(int x, int y) {
int fx = find(x), fy = find(y);
if (fx != fy) {
if (sze[fx] > sze[fy]) {
swap(fx, fy);
}
fa[fx] = fy;
sze[fy] += sze[fx];
return true;
}
return false;
}
bool same(int x, int y) {
return find(x) == find(y);
}
} ufs;
int mv[4][2] = {
{0, -1},
{0, 1},
{1, 0},
{-1, 0},
};
class Solution {
public:
int n, m;
int id(int x, int y) {
return x * m + y;
}
vector<int> maxPoints(vector<vector<int>> &grid, vector<int> &queries) {
int n = int(grid.size());
int m = int(grid[0].size());
int q = int(queries.size());
this->n = n;
this->m = m;
int nn = n * m;
ufs.init(nn + 5);
auto node = vector<tuple<int, int, int>>();
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
node.push_back(make_tuple(grid[i][j], i, j));
}
}
sort(all(node));
auto qq = vector<tuple<int, int>>();
for (int i = 0; i < q; i++) {
qq.push_back(make_tuple(queries[i], i));
}
sort(all(qq));
auto res = vector<int>(q, 0);
for (int i = 0, ix = 0; i < q; i++) {
const auto [qv, qx] = qq[i];
while (ix < nn && get<0>(node[ix]) < qv) {
const auto [v, x, y] = node[ix];
for (int j = 0; j < 4; j++) {
int nx = x + mv[j][0];
int ny = y + mv[j][1];
if (nx >= 0 && nx < n && ny >= 0 && ny < m && grid[nx][ny] < qv) {
ufs.merge(id(x, y), id(nx, ny));
}
}
++ix;
}
if (qv > grid[0][0]) {
res[qx] = ufs.sze[ufs.find(0)];
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif