weekly-contest-209

A

Statement

简体中文English

Metadata

• Link: 特殊数组的特征值
• Difficulty: Easy
• Tag: 数组 二分查找 排序

给你一个非负整数数组 nums 。如果存在一个数 x ，使得 nums 中恰好有 x 个元素 大于或者等于 x ，那么就称 nums 是一个 特殊数组 ，而 x 是该数组的 特征值 。

注意： x 不必 是 nums 的中的元素。

如果数组 nums 是一个 特殊数组 ，请返回它的特征值 x 。否则，返回 -1 。可以证明的是，如果 nums 是特殊数组，那么其特征值 x 是 唯一的 。

 

示例 1：

输入：nums = [3,5]
输出：2
解释：有 2 个元素（3 和 5）大于或等于 2 。

示例 2：

输入：nums = [0,0]
输出：-1
解释：没有满足题目要求的特殊数组，故而也不存在特征值 x 。
如果 x = 0，应该有 0 个元素 >= x，但实际有 2 个。
如果 x = 1，应该有 1 个元素 >= x，但实际有 0 个。
如果 x = 2，应该有 2 个元素 >= x，但实际有 0 个。
x 不能取更大的值，因为 nums 中只有两个元素。

示例 3：

输入：nums = [0,4,3,0,4]
输出：3
解释：有 3 个元素大于或等于 3 。

示例 4：

输入：nums = [3,6,7,7,0]
输出：-1

 

提示：

• 1 <= nums.length <= 100
• 0 <= nums[i] <= 1000

Metadata

• Link: Special Array With X Elements Greater Than or Equal X
• Difficulty: Easy
• Tag: Array Binary Search Sorting

You are given an array nums of non-negative integers. nums is considered special if there exists a number x such that there are exactly x numbers in nums that are greater than or equal to x.

Notice that x does not have to be an element in nums.

Return x if the array is special, otherwise, return -1. It can be proven that if nums is special, the value for x is unique.

 

Example 1:

Input: nums = [3,5]
Output: 2
Explanation: There are 2 values (3 and 5) that are greater than or equal to 2.

Example 2:

Input: nums = [0,0]
Output: -1
Explanation: No numbers fit the criteria for x.
If x = 0, there should be 0 numbers >= x, but there are 2.
If x = 1, there should be 1 number >= x, but there are 0.
If x = 2, there should be 2 numbers >= x, but there are 0.
x cannot be greater since there are only 2 numbers in nums.

Example 3:

Input: nums = [0,4,3,0,4]
Output: 3
Explanation: There are 3 values that are greater than or equal to 3.

 

Constraints:

• 1 <= nums.length <= 100
• 0 <= nums[i] <= 1000

Solution

C++

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
int n;

class Solution {
public:
    int specialArray(vector<int> &nums) {
        sort(all(nums));
        n = SZ(nums);
        int pos = 0;
        for (int i = 0; i <= 1000; ++i) {
            while (pos < n && nums[pos] < i) ++pos;
            if (n - pos == i)
                return i;
        }
        return -1;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

简体中文English

Metadata

• Link: 奇偶树
• Difficulty: Medium
• Tag: 树 广度优先搜索 二叉树

如果一棵二叉树满足下述几个条件，则可以称为 奇偶树 ：

• 二叉树根节点所在层下标为 0 ，根的子节点所在层下标为 1 ，根的孙节点所在层下标为 2 ，依此类推。
• 偶数下标 层上的所有节点的值都是 奇 整数，从左到右按顺序 严格递增
• 奇数下标 层上的所有节点的值都是 偶 整数，从左到右按顺序 严格递减

给你二叉树的根节点，如果二叉树为 奇偶树 ，则返回 true ，否则返回 false 。

 

示例 1：

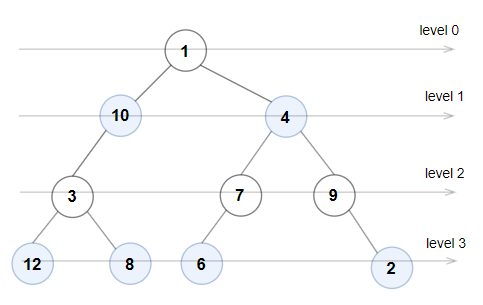
输入：root = [1,10,4,3,null,7,9,12,8,6,null,null,2]
输出：true
解释：每一层的节点值分别是：
0 层：[1]
1 层：[10,4]
2 层：[3,7,9]
3 层：[12,8,6,2]
由于 0 层和 2 层上的节点值都是奇数且严格递增，而 1 层和 3 层上的节点值都是偶数且严格递减，因此这是一棵奇偶树。

示例 2：

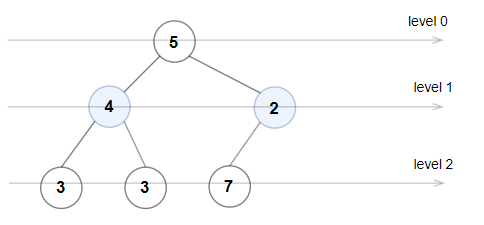
输入：root = [5,4,2,3,3,7]
输出：false
解释：每一层的节点值分别是：
0 层：[5]
1 层：[4,2]
2 层：[3,3,7]
2 层上的节点值不满足严格递增的条件，所以这不是一棵奇偶树。

示例 3：

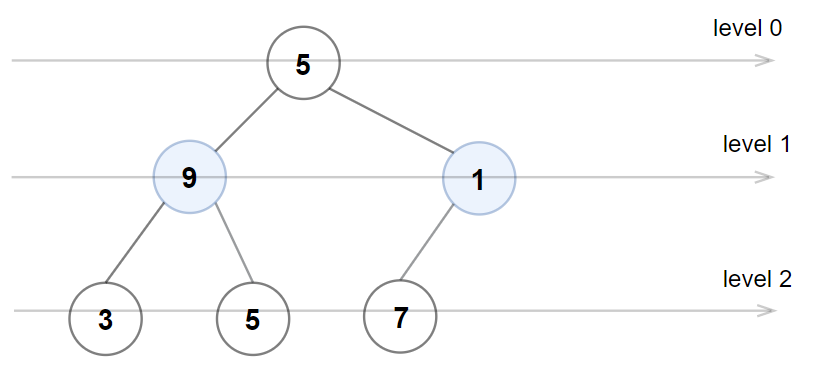
输入：root = [5,9,1,3,5,7]
输出：false
解释：1 层上的节点值应为偶数。

示例 4：

输入：root = [1]
输出：true

示例 5：

输入：root = [11,8,6,1,3,9,11,30,20,18,16,12,10,4,2,17]
输出：true

 

提示：

• 树中节点数在范围 [1, 105] 内
• 1 <= Node.val <= 106

Metadata

• Link: Even Odd Tree
• Difficulty: Medium
• Tag: Tree Breadth-First Search Binary Tree

A binary tree is named Even-Odd if it meets the following conditions:

• The root of the binary tree is at level index 0, its children are at level index 1, their children are at level index 2, etc.
• For every even-indexed level, all nodes at the level have odd integer values in strictly increasing order (from left to right).
• For every odd-indexed level, all nodes at the level have even integer values in strictly decreasing order (from left to right).

Given the root of a binary tree, return true if the binary tree is Even-Odd, otherwise return false.

 

Example 1:

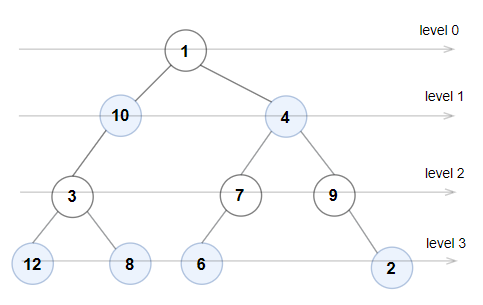
Input: root = [1,10,4,3,null,7,9,12,8,6,null,null,2]
Output: true
Explanation: The node values on each level are:
Level 0: [1]
Level 1: [10,4]
Level 2: [3,7,9]
Level 3: [12,8,6,2]
Since levels 0 and 2 are all odd and increasing and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.

Example 2:

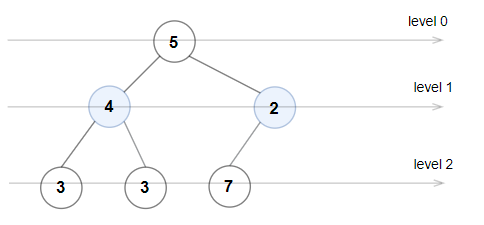
Input: root = [5,4,2,3,3,7]
Output: false
Explanation: The node values on each level are:
Level 0: [5]
Level 1: [4,2]
Level 2: [3,3,7]
Node values in level 2 must be in strictly increasing order, so the tree is not Even-Odd.

Example 3:

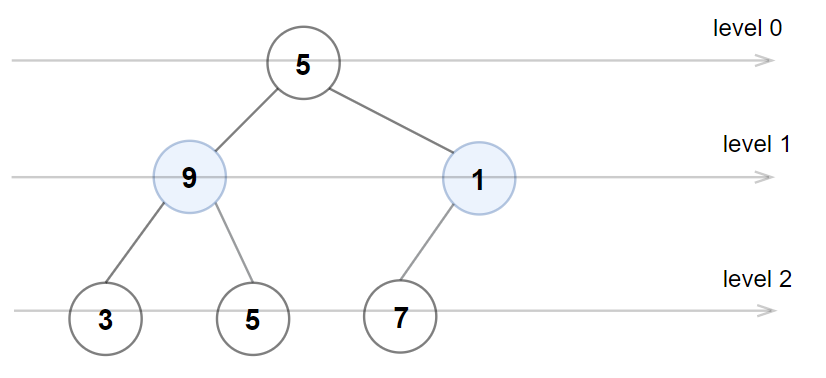
Input: root = [5,9,1,3,5,7]
Output: false
Explanation: Node values in the level 1 should be even integers.

 

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 1 <= Node.val <= 106

Solution

C++

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
constexpr int INF = 0x3f3f3f3f;
int n;

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isEvenOddTree(TreeNode *root) {
        vector<vector<int>> vec;
        queue<TreeNode *> que;
        que.push(root);
        while (!que.empty()) {
            queue<TreeNode *> _que;
            vector<int> _vec;
            while (!que.empty()) {
                TreeNode *rt = que.front();
                que.pop();
                _vec.push_back(rt->val);
                if (rt->left)
                    _que.push(rt->left);
                if (rt->right)
                    _que.push(rt->right);
            }
            que = _que;
            vec.push_back(_vec);
        }
        for (int i = 0; i < SZ(vec); ++i) {
            int f = i & 1 ^ 1;
            int pre = f ? 0 : INF;
            for (auto &x : vec[i]) {
                if ((x & 1) != f)
                    return false;
                if (f && x <= pre)
                    return false;
                if (!f && x >= pre)
                    return false;
                pre = x;
            }
        }
        return true;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

简体中文English

Metadata

• Link: 可见点的最大数目
• Difficulty: Hard
• Tag: 几何 数组 数学 排序 滑动窗口

给你一个点数组 points 和一个表示角度的整数 angle ，你的位置是 location ，其中 location = [posx, posy] 且 points[i] = [xi, yi] 都表示 X-Y 平面上的整数坐标。

最开始，你面向东方进行观测。你 不能 进行移动改变位置，但可以通过 自转 调整观测角度。换句话说，posx 和 posy 不能改变。你的视野范围的角度用 angle 表示， 这决定了你观测任意方向时可以多宽。设 d 为你逆时针自转旋转的度数，那么你的视野就是角度范围 [d - angle/2, d + angle/2] 所指示的那片区域。

对于每个点，如果由该点、你的位置以及从你的位置直接向东的方向形成的角度 位于你的视野中 ，那么你就可以看到它。

同一个坐标上可以有多个点。你所在的位置也可能存在一些点，但不管你的怎么旋转，总是可以看到这些点。同时，点不会阻碍你看到其他点。

返回你能看到的点的最大数目。

 

示例 1：

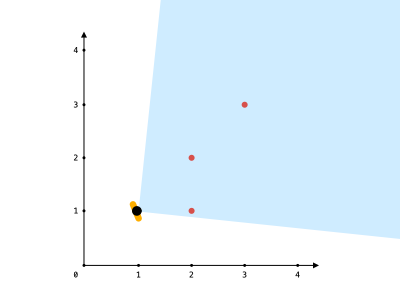
输入：points = [[2,1],[2,2],[3,3]], angle = 90, location = [1,1]
输出：3
解释：阴影区域代表你的视野。在你的视野中，所有的点都清晰可见，尽管 [2,2] 和 [3,3]在同一条直线上，你仍然可以看到 [3,3] 。

示例 2：

输入：points = [[2,1],[2,2],[3,4],[1,1]], angle = 90, location = [1,1]
输出：4
解释：在你的视野中，所有的点都清晰可见，包括你所在位置的那个点。

示例 3：

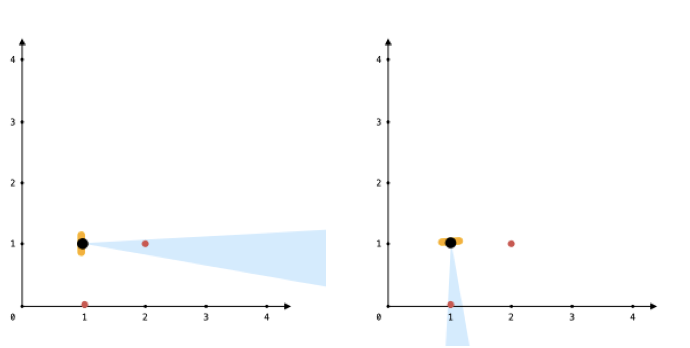
输入：points = [[1,0],[2,1]], angle = 13, location = [1,1]
输出：1
解释：如图所示，你只能看到两点之一。

 

提示：

• 1 <= points.length <= 105
• points[i].length == 2
• location.length == 2
• 0 <= angle < 360
• 0 <= posx, posy, xi, yi <= 100

Metadata

• Link: Maximum Number of Visible Points
• Difficulty: Hard
• Tag: Geometry Array Math Sorting Sliding Window

You are given an array points, an integer angle, and your location, where location = [posx, posy] and points[i] = [xi, yi] both denote integral coordinates on the X-Y plane.

Initially, you are facing directly east from your position. You cannot move from your position, but you can rotate. In other words, posx and posy cannot be changed. Your field of view in degrees is represented by angle, determining how wide you can see from any given view direction. Let d be the amount in degrees that you rotate counterclockwise. Then, your field of view is the inclusive range of angles [d - angle/2, d + angle/2].

You can see some set of points if, for each point, the angle formed by the point, your position, and the immediate east direction from your position is in your field of view.

There can be multiple points at one coordinate. There may be points at your location, and you can always see these points regardless of your rotation. Points do not obstruct your vision to other points.

Return the maximum number of points you can see.

 

Example 1:

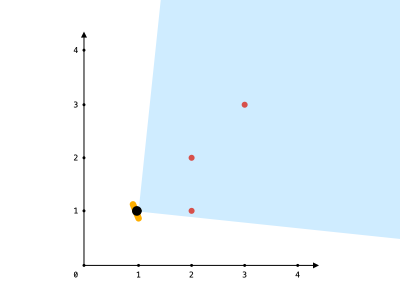
Input: points = [[2,1],[2,2],[3,3]], angle = 90, location = [1,1]
Output: 3
Explanation: The shaded region represents your field of view. All points can be made visible in your field of view, including [3,3] even though [2,2] is in front and in the same line of sight.

Example 2:

Input: points = [[2,1],[2,2],[3,4],[1,1]], angle = 90, location = [1,1]
Output: 4
Explanation: All points can be made visible in your field of view, including the one at your location.

Example 3:

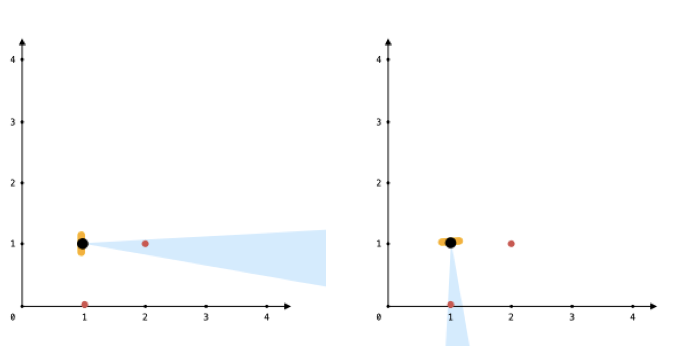
Input: points = [[1,0],[2,1]], angle = 13, location = [1,1]
Output: 1
Explanation: You can only see one of the two points, as shown above.

 

Constraints:

• 1 <= points.length <= 105
• points[i].length == 2
• location.length == 2
• 0 <= angle < 360
• 0 <= posx, posy, xi, yi <= 100

D

Statement

简体中文English

Metadata

• Link: 使整数变为 0 的最少操作次数
• Difficulty: Hard
• Tag: 位运算 记忆化搜索 动态规划

给你一个整数 n，你需要重复执行多次下述操作将其转换为 0 ：

• 翻转 n 的二进制表示中最右侧位（第 0 位）。
• 如果第 (i-1) 位为 1 且从第 (i-2) 位到第 0 位都为 0，则翻转 n 的二进制表示中的第 i 位。

返回将 n 转换为 0 的最小操作次数。

 

示例 1：

输入：n = 0
输出：0

示例 2：

输入：n = 3
输出：2
解释：3 的二进制表示为 "11"
"11" -> "01" ，执行的是第 2 种操作，因为第 0 位为 1 。
"01" -> "00" ，执行的是第 1 种操作。

示例 3：

输入：n = 6
输出：4
解释：6 的二进制表示为 "110".
"110" -> "010" ，执行的是第 2 种操作，因为第 1 位为 1 ，第 0 到 0 位为 0 。
"010" -> "011" ，执行的是第 1 种操作。
"011" -> "001" ，执行的是第 2 种操作，因为第 0 位为 1 。
"001" -> "000" ，执行的是第 1 种操作。

示例 4：

输入：n = 9
输出：14

示例 5：

输入：n = 333
输出：393

 

提示：

• 0 <= n <= 109

Metadata

• Link: Minimum One Bit Operations to Make Integers Zero
• Difficulty: Hard
• Tag: Bit Manipulation Memoization Dynamic Programming

Given an integer n, you must transform it into 0 using the following operations any number of times:

• Change the rightmost (0th) bit in the binary representation of n.
• Change the ith bit in the binary representation of n if the (i-1)th bit is set to 1 and the (i-2)th through 0th bits are set to 0.

Return the minimum number of operations to transform n into 0.

 

Example 1:

Input: n = 3
Output: 2
Explanation: The binary representation of 3 is "11".
"11" -> "01" with the 2nd operation since the 0th bit is 1.
"01" -> "00" with the 1st operation.

Example 2:

Input: n = 6
Output: 4
Explanation: The binary representation of 6 is "110".
"110" -> "010" with the 2nd operation since the 1st bit is 1 and 0th through 0th bits are 0.
"010" -> "011" with the 1st operation.
"011" -> "001" with the 2nd operation since the 0th bit is 1.
"001" -> "000" with the 1st operation.

 

Constraints:

• 0 <= n <= 109

Solution

C++

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
int n;

map<int, int> mp;

int dfs(int n) {
    if (!n)
        return 0;
    if (n == 1)
        return mp[n] = 1;
    if (mp.count(n))
        return mp[n];
    int f = 1 + dfs(n ^ 1);
    int x = __builtin_ffs(n);
    if (x <= 30)
        chmin(f, 1 + dfs(n ^ (1 << x)));
    return mp[n] = f;
}

class Solution {
public:
    int minimumOneBitOperations(int n) {
        mp.clear();
        return dfs(n);
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

---

最后更新: October 11, 2023