weekly-contest-207
A
Statement
Metadata
- Link: 重新排列单词间的空格
- Difficulty: Easy
- Tag:
字符串
给你一个字符串 text ,该字符串由若干被空格包围的单词组成。每个单词由一个或者多个小写英文字母组成,并且两个单词之间至少存在一个空格。题目测试用例保证 text 至少包含一个单词 。
请你重新排列空格,使每对相邻单词之间的空格数目都 相等 ,并尽可能 最大化 该数目。如果不能重新平均分配所有空格,请 将多余的空格放置在字符串末尾 ,这也意味着返回的字符串应当与原 text 字符串的长度相等。
返回 重新排列空格后的字符串 。
示例 1:
输入:text = " this is a sentence "
输出:"this is a sentence"
解释:总共有 9 个空格和 4 个单词。可以将 9 个空格平均分配到相邻单词之间,相邻单词间空格数为:9 / (4-1) = 3 个。
示例 2:
输入:text = " practice makes perfect"
输出:"practice makes perfect "
解释:总共有 7 个空格和 3 个单词。7 / (3-1) = 3 个空格加上 1 个多余的空格。多余的空格需要放在字符串的末尾。
示例 3:
输入:text = "hello world"
输出:"hello world"
示例 4:
输入:text = " walks udp package into bar a"
输出:"walks udp package into bar a "
示例 5:
输入:text = "a"
输出:"a"
提示:
1 <= text.length <= 100text由小写英文字母和' '组成text中至少包含一个单词
Metadata
- Link: Rearrange Spaces Between Words
- Difficulty: Easy
- Tag:
String
You are given a string text of words that are placed among some number of spaces. Each word consists of one or more lowercase English letters and are separated by at least one space. It's guaranteed that text contains at least one word.
Rearrange the spaces so that there is an equal number of spaces between every pair of adjacent words and that number is maximized. If you cannot redistribute all the spaces equally, place the extra spaces at the end, meaning the returned string should be the same length as text.
Return the string after rearranging the spaces.
Example 1:
Input: text = " this is a sentence "
Output: "this is a sentence"
Explanation: There are a total of 9 spaces and 4 words. We can evenly divide the 9 spaces between the words: 9 / (4-1) = 3 spaces.
Example 2:
Input: text = " practice makes perfect"
Output: "practice makes perfect "
Explanation: There are a total of 7 spaces and 3 words. 7 / (3-1) = 3 spaces plus 1 extra space. We place this extra space at the end of the string.
Constraints:
1 <= text.length <= 100textconsists of lowercase English letters and' '.textcontains at least one word.
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n;
class Solution {
public:
string reorderSpaces(string text) {
n = SZ(text);
int cnt = 0;
vector<string> res;
string t = "";
for (auto &ch : text) {
if (ch == ' ') {
++cnt;
if (SZ(t))
res.push_back(t);
t.clear();
} else {
t += ch;
}
}
if (SZ(t))
res.push_back(t);
t.clear();
string s = "";
int m = SZ(res);
if (m == 1) {
s += res[0];
s += string(cnt, ' ');
return s;
} else {
int need = cnt / (m - 1);
s += res[0];
for (int i = 1; i < m; ++i) {
s += string(need, ' ');
s += res[i];
}
int remind = cnt - need * (m - 1);
s += string(remind, ' ');
return s;
}
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 拆分字符串使唯一子字符串的数目最大
- Difficulty: Medium
- Tag:
哈希表字符串回溯
给你一个字符串 s ,请你拆分该字符串,并返回拆分后唯一子字符串的最大数目。
字符串 s 拆分后可以得到若干 非空子字符串 ,这些子字符串连接后应当能够还原为原字符串。但是拆分出来的每个子字符串都必须是 唯一的 。
注意:子字符串 是字符串中的一个连续字符序列。
示例 1:
输入:s = "ababccc"
输出:5
解释:一种最大拆分方法为 ['a', 'b', 'ab', 'c', 'cc'] 。像 ['a', 'b', 'a', 'b', 'c', 'cc'] 这样拆分不满足题目要求,因为其中的 'a' 和 'b' 都出现了不止一次。
示例 2:
输入:s = "aba"
输出:2
解释:一种最大拆分方法为 ['a', 'ba'] 。
示例 3:
输入:s = "aa"
输出:1
解释:无法进一步拆分字符串。
提示:
-
1 <= s.length <= 16 -
s仅包含小写英文字母
Metadata
- Link: Split a String Into the Max Number of Unique Substrings
- Difficulty: Medium
- Tag:
Hash TableStringBacktracking
Given a string s, return the maximum number of unique substrings that the given string can be split into.
You can split string s into any list of non-empty substrings, where the concatenation of the substrings forms the original string. However, you must split the substrings such that all of them are unique.
A substring is a contiguous sequence of characters within a string.
Example 1:
Input: s = "ababccc"
Output: 5
Explanation: One way to split maximally is ['a', 'b', 'ab', 'c', 'cc']. Splitting like ['a', 'b', 'a', 'b', 'c', 'cc'] is not valid as you have 'a' and 'b' multiple times.
Example 2:
Input: s = "aba"
Output: 2
Explanation: One way to split maximally is ['a', 'ba'].
Example 3:
Input: s = "aa"
Output: 1
Explanation: It is impossible to split the string any further.
Constraints:
-
1 <= s.length <= 16 -
scontains only lower case English letters.
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n, res;
string s;
void dfs(unordered_set<string> mp, string t, int cur) {
//<string, int> mp, string t, int cur) {
if (cur == n) {
chmax(res, SZ(mp));
} else {
if (cur == n - 1) {
t += s[cur];
if (mp.find(t) == mp.end()) {
chmax(res, SZ(mp) + 1);
}
} else {
if (SZ(mp) + n - cur < res)
return;
t += s[cur];
dfs(mp, t, cur + 1);
if (mp.find(t) == mp.end()) {
mp.insert(t);
dfs(mp, "", cur + 1);
}
}
}
}
class Solution {
public:
int maxUniqueSplit(string _s) {
s = _s;
n = SZ(s);
res = 1;
dfs(unordered_set<string>(), "", 0);
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 矩阵的最大非负积
- Difficulty: Medium
- Tag:
数组动态规划矩阵
给你一个大小为 rows x cols 的矩阵 grid 。最初,你位于左上角 (0, 0) ,每一步,你可以在矩阵中 向右 或 向下 移动。
在从左上角 (0, 0) 开始到右下角 (rows - 1, cols - 1) 结束的所有路径中,找出具有 最大非负积 的路径。路径的积是沿路径访问的单元格中所有整数的乘积。
返回 最大非负积 对 109 + 7 取余 的结果。如果最大积为负数,则返回 -1 。
注意,取余是在得到最大积之后执行的。
示例 1:
输入:grid = [[-1,-2,-3],
[-2,-3,-3],
[-3,-3,-2]]
输出:-1
解释:从 (0, 0) 到 (2, 2) 的路径中无法得到非负积,所以返回 -1
示例 2:
输入:grid = [[1,-2,1],
[1,-2,1],
[3,-4,1]]
输出:8
解释:最大非负积对应的路径已经用粗体标出 (1 * 1 * -2 * -4 * 1 = 8)
示例 3:
输入:grid = [[1, 3],
[0,-4]]
输出:0
解释:最大非负积对应的路径已经用粗体标出 (1 * 0 * -4 = 0)
示例 4:
输入:grid = [[ 1, 4,4,0],
[-2, 0,0,1],
[ 1,-1,1,1]]
输出:2
解释:最大非负积对应的路径已经用粗体标出 (1 * -2 * 1 * -1 * 1 * 1 = 2)
提示:
1 <= rows, cols <= 15-4 <= grid[i][j] <= 4
Metadata
- Link: Maximum Non Negative Product in a Matrix
- Difficulty: Medium
- Tag:
ArrayDynamic ProgrammingMatrix
You are given a m x n matrix grid. Initially, you are located at the top-left corner (0, 0), and in each step, you can only move right or down in the matrix.
Among all possible paths starting from the top-left corner (0, 0) and ending in the bottom-right corner (m - 1, n - 1), find the path with the maximum non-negative product. The product of a path is the product of all integers in the grid cells visited along the path.
Return the maximum non-negative product modulo 109 + 7. If the maximum product is negative, return -1.
Notice that the modulo is performed after getting the maximum product.
Example 1:
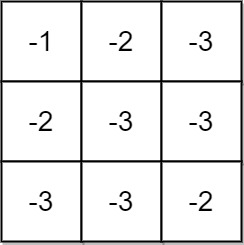
Input: grid = [[-1,-2,-3],[-2,-3,-3],[-3,-3,-2]]
Output: -1
Explanation: It is not possible to get non-negative product in the path from (0, 0) to (2, 2), so return -1.
Example 2:
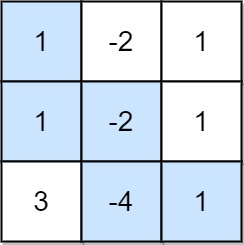
Input: grid = [[1,-2,1],[1,-2,1],[3,-4,1]]
Output: 8
Explanation: Maximum non-negative product is shown (1 * 1 * -2 * -4 * 1 = 8).
Example 3:
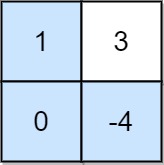
Input: grid = [[1,3],[0,-4]]
Output: 0
Explanation: Maximum non-negative product is shown (1 * 0 * -4 = 0).
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 15-4 <= grid[i][j] <= 4
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e2 + 10;
int n, m;
ll f[N][N][2];
int Move[][2] = {-1, 0, 0, -1};
bool ok(int x, int y) {
if (x < 0 || x >= n || y < 0 || y >= m)
return false;
return true;
}
class Solution {
public:
int maxProductPath(vector<vector<int>> &grid) {
n = SZ(grid);
m = SZ(grid[0]);
memset(f, -1, sizeof f);
if (grid[0][0] >= 0)
f[0][0][0] = grid[0][0];
else
f[0][0][1] = abs(grid[0][0]);
int zero = grid[0][0] == 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
zero += grid[i][j] == 0;
if (i || j) {
int p = (grid[i][j] < 0);
for (int k = 0; k < 2; ++k) {
int nx = i + Move[k][0];
int ny = j + Move[k][1];
if (ok(nx, ny) && grid[nx][ny] != 0) {
if (f[nx][ny][0] != -1) {
chmax(f[i][j][p], f[nx][ny][0] * abs(grid[i][j]));
}
if (f[nx][ny][1] != -1) {
chmax(f[i][j][p ^ 1], f[nx][ny][1] * abs(grid[i][j]));
}
}
}
}
}
}
int res = -1;
if (zero)
res = 0;
if (f[n - 1][m - 1][0] != -1)
res = f[n - 1][m - 1][0] % mod;
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 连通两组点的最小成本
- Difficulty: Hard
- Tag:
位运算数组动态规划状态压缩矩阵
给你两组点,其中第一组中有 size1 个点,第二组中有 size2 个点,且 size1 >= size2 。
任意两点间的连接成本 cost 由大小为 size1 x size2 矩阵给出,其中 cost[i][j] 是第一组中的点 i 和第二组中的点 j 的连接成本。如果两个组中的每个点都与另一组中的一个或多个点连接,则称这两组点是连通的。换言之,第一组中的每个点必须至少与第二组中的一个点连接,且第二组中的每个点必须至少与第一组中的一个点连接。
返回连通两组点所需的最小成本。
示例 1:
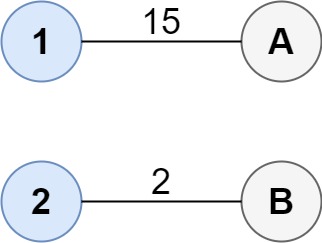
输入:cost = [[15, 96], [36, 2]]
输出:17
解释:连通两组点的最佳方法是:
1–A
2–B
总成本为 17 。
示例 2:
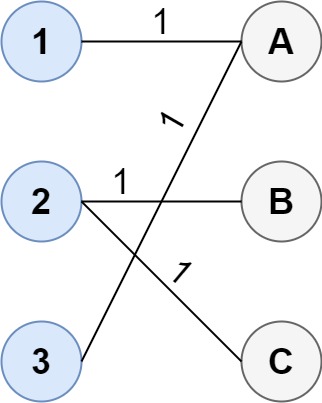
输入:cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
输出:4
解释:连通两组点的最佳方法是:
1–A
2–B
2–C
3–A
最小成本为 4 。
请注意,虽然有多个点连接到第一组中的点 2 和第二组中的点 A ,但由于题目并不限制连接点的数目,所以只需要关心最低总成本。示例 3:
输入:cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]]
输出:10
提示:
size1 == cost.lengthsize2 == cost[i].length1 <= size1, size2 <= 12size1 >= size20 <= cost[i][j] <= 100
Metadata
- Link: Minimum Cost to Connect Two Groups of Points
- Difficulty: Hard
- Tag:
Bit ManipulationArrayDynamic ProgrammingBitmaskMatrix
You are given two groups of points where the first group has size1 points, the second group has size2 points, and size1 >= size2.
The cost of the connection between any two points are given in an size1 x size2 matrix where cost[i][j] is the cost of connecting point i of the first group and point j of the second group. The groups are connected if each point in both groups is connected to one or more points in the opposite group. In other words, each point in the first group must be connected to at least one point in the second group, and each point in the second group must be connected to at least one point in the first group.
Return the minimum cost it takes to connect the two groups.
Example 1:
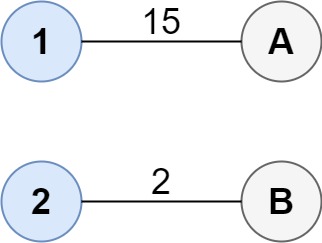
Input: cost = [[15, 96], [36, 2]]
Output: 17
Explanation: The optimal way of connecting the groups is:
1–A
2–B
This results in a total cost of 17.
Example 2:
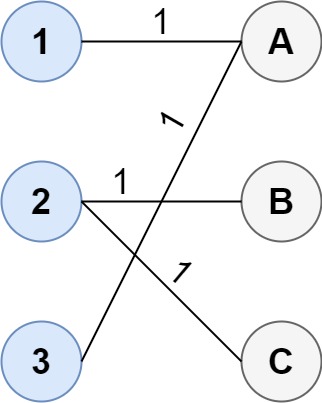
Input: cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
Output: 4
Explanation: The optimal way of connecting the groups is:
1–A
2–B
2–C
3–A
This results in a total cost of 4.
Note that there are multiple points connected to point 2 in the first group and point A in the second group. This does not matter as there is no limit to the number of points that can be connected. We only care about the minimum total cost.
Example 3:
Input: cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]]
Output: 10
Constraints:
size1 == cost.lengthsize2 == cost[i].length1 <= size1, size2 <= 12size1 >= size20 <= cost[i][j] <= 100
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e2 + 10;
constexpr int INF = 0x3f3f3f3f;
int n, m, f[N], g[2][1 << 13];
class Solution {
public:
int connectTwoGroups(vector<vector<int>> &cost) {
n = SZ(cost);
m = SZ(cost[0]);
int res = INF;
memset(f, 0x3f, sizeof f);
memset(g, 0x3f, sizeof g);
g[1][0] = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
chmin(f[j], cost[i][j]);
}
}
for (int i = 0; i < n; ++i) {
int p = i & 1;
memset(g[p], 0x3f, sizeof g[p]);
for (int j = 0; j < m; ++j) {
for (int S = 0; S < 1 << m; ++S) {
chmin(g[p][S | (1 << j)], g[p ^ 1][S] + cost[i][j]);
}
}
}
int p = (n - 1) & 1;
for (int S = 0; S < 1 << m; ++S) {
int add = 0;
for (int i = 0; i < m; ++i) {
if (!((S >> i) & 1)) {
add += f[i];
}
}
chmin(res, g[p][S] + add);
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif