biweekly-contest-81

A

Statement

简体中文English

Metadata

Link: 统计星号
Difficulty: Easy
Tag:

给你一个字符串 s ，每两个连续竖线 '|' 为一对。换言之，第一个和第二个 '|' 为一对，第三个和第四个 '|' 为一对，以此类推。

请你返回不在竖线对之间，s 中 '*' 的数目。

注意，每个竖线 '|' 都会恰好属于一个对。

示例 1：

输入：s = "l|*e*et|c**o|*de|"
输出：2
解释：不在竖线对之间的字符加粗加斜体后，得到字符串："l|*e*et|c**o|*de|" 。
第一和第二条竖线 '|' 之间的字符不计入答案。
同时，第三条和第四条竖线 '|' 之间的字符也不计入答案。
不在竖线对之间总共有 2 个星号，所以我们返回 2 。

示例 2：

输入：s = "iamprogrammer"
输出：0
解释：在这个例子中，s 中没有星号。所以返回 0 。

示例 3：

输入：s = "yo|uar|e**|b|e***au|tifu|l"
输出：5
解释：需要考虑的字符加粗加斜体后："yo|uar|e**|b|e***au|tifu|l" 。不在竖线对之间总共有 5 个星号。所以我们返回 5 。

提示：

1 <= s.length <= 1000
s 只包含小写英文字母，竖线 '|' 和星号 '*' 。
s 包含偶数个竖线 '|' 。

Metadata

Link: Count Asterisks
Difficulty: Easy
Tag:

You are given a string s, where every two consecutive vertical bars '|' are grouped into a pair. In other words, the 1^st and 2^nd '|' make a pair, the 3^rd and 4^th '|' make a pair, and so forth.

Return the number of '*' in s, excluding the '*' between each pair of '|'.

Note that each '|' will belong to exactly one pair.

Example 1:

Input: s = "l|*e*et|c**o|*de|"
Output: 2
Explanation: The considered characters are underlined: "l|*e*et|c**o|*de|".
The characters between the first and second '|' are excluded from the answer.
Also, the characters between the third and fourth '|' are excluded from the answer.
There are 2 asterisks considered. Therefore, we return 2.

Example 2:

Input: s = "iamprogrammer"
Output: 0
Explanation: In this example, there are no asterisks in s. Therefore, we return 0.

Example 3:

Input: s = "yo|uar|e**|b|e***au|tifu|l"
Output: 5
Explanation: The considered characters are underlined: "yo|uar|e**|b|e***au|tifu|l". There are 5 asterisks considered. Therefore, we return 5.

Constraints:

1 <= s.length <= 1000
s consists of lowercase English letters, vertical bars '|', and asterisks '*'.
s contains an even number of vertical bars '|'.

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    int countAsterisks(const string &s) {
        int flag = 1;
        int res = 0;
        for (const char &c : s) {
            if (c == '*') {
                res += flag;
            }

            if (c == '|') {
                flag ^= 1;
            }
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

简体中文English

Metadata

Link: 统计无向图中无法互相到达点对数
Difficulty: Medium
Tag:

给你一个整数 n ，表示一张 无向图 中有 n 个节点，编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ，其中 edges[i] = [a_i, b_i] 表示节点 a_i 和 b_i 之间有一条无向边。

请你返回 无法互相到达 的不同 点对数目 。

示例 1：

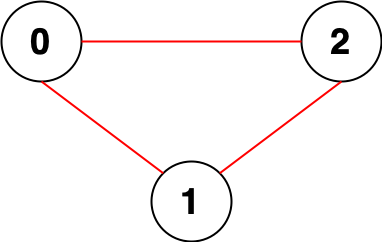
输入：n = 3, edges = [[0,1],[0,2],[1,2]]
输出：0
解释：所有点都能互相到达，意味着没有点对无法互相到达，所以我们返回 0 。

示例 2：

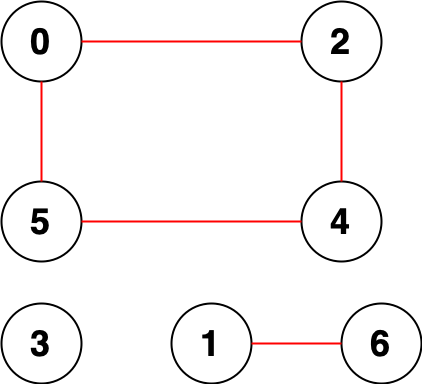
输入：n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出：14
解释：总共有 14 个点对互相无法到达：
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14 。

提示：

1 <= n <= 10⁵
0 <= edges.length <= 2 * 10⁵
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
不会有重复边。

Metadata

Link: Count Unreachable Pairs of Nodes in an Undirected Graph
Difficulty: Medium
Tag:

You are given an integer n. There is an undirected graph with n nodes, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [a_i, b_i] denotes that there exists an undirected edge connecting nodes a_i and b_i.

Return the number of pairs of different nodes that are unreachable from each other.

Example 1:

Input: n = 3, edges = [[0,1],[0,2],[1,2]]
Output: 0
Explanation: There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.

Example 2:

Input: n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
Output: 14
Explanation: There are 14 pairs of nodes that are unreachable from each other:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]].
Therefore, we return 14.

Constraints:

1 <= n <= 10⁵
0 <= edges.length <= 2 * 10⁵
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
There are no repeated edges.

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

constexpr int N = 1e5 + 10;

struct UFS {
    int fa[N], rk[N], sz[N];
    void init(int n) {
        memset(fa, 0, sizeof(fa[0]) * (n + 5));
        memset(rk, 0, sizeof(rk[0]) * (n + 5));
        for (int i = 1; i <= n; i++) {
            sz[i] = 1;
        }
    }
    int find(int x) {
        return fa[x] == 0 ? x : fa[x] = find(fa[x]);
    }
    bool merge(int x, int y) {
        int fx = find(x), fy = find(y);
        if (fx != fy) {
            if (rk[fx] > rk[fy])
                swap(fx, fy);
            fa[fx] = fy;
            if (rk[fx] == rk[fy])
                ++rk[fy];
            sz[fy] += sz[fx];
            return true;
        }
        return false;
    }
    bool same(int x, int y) {
        return find(x) == find(y);
    }
} ufs;

class Solution {
public:
    long long countPairs(int n, vector<vector<int>> &edges) {
        ufs.init(n);

        for (auto &e : edges) {
            ufs.merge(e[0] + 1, e[1] + 1);
        }

        auto f = vector<int>();

        for (int i = 1; i <= n; i++) {
            if (ufs.find(i) == i) {
                f.push_back(ufs.sz[i]);
            }
        }

        ll sum = f[0];
        ll res = 0;
        for (size_t i = 1; i < f.size(); i++) {
            res += f[i] * sum;
            sum += f[i];
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

简体中文English

Metadata

Link: 操作后的最大异或和
Difficulty: Medium
Tag:

给你一个下标从 0 开始的整数数组 nums 。一次操作中，选择任意非负整数 x 和一个下标 i ，更新 nums[i] 为 nums[i] AND (nums[i] XOR x) 。

注意，AND 是逐位与运算，XOR 是逐位异或运算。

请你执行 任意次 更新操作，并返回 nums 中所有元素最大逐位异或和。

示例 1：

输入：nums = [3,2,4,6]
输出：7
解释：选择 x = 4 和 i = 3 进行操作，num[3] = 6 AND (6 XOR 4) = 6 AND 2 = 2 。
现在，nums = [3, 2, 4, 2] 且所有元素逐位异或得到 3 XOR 2 XOR 4 XOR 2 = 7 。
可知 7 是能得到的最大逐位异或和。
注意，其他操作可能也能得到逐位异或和 7 。

示例 2：

输入：nums = [1,2,3,9,2]
输出：11
解释：执行 0 次操作。
所有元素的逐位异或和为 1 XOR 2 XOR 3 XOR 9 XOR 2 = 11 。
可知 11 是能得到的最大逐位异或和。

提示：

1 <= nums.length <= 10⁵
0 <= nums[i] <= 10⁸

Metadata

Link: Maximum XOR After Operations
Difficulty: Medium
Tag:

You are given a 0-indexed integer array nums. In one operation, select any non-negative integer x and an index i, then update nums[i] to be equal to nums[i] AND (nums[i] XOR x).

Note that AND is the bitwise AND operation and XOR is the bitwise XOR operation.

Return the maximum possible bitwise XOR of all elements of nums after applying the operation any number of times.

Example 1:

Input: nums = [3,2,4,6]
Output: 7
Explanation: Apply the operation with x = 4 and i = 3, num[3] = 6 AND (6 XOR 4) = 6 AND 2 = 2.
Now, nums = [3, 2, 4, 2] and the bitwise XOR of all the elements = 3 XOR 2 XOR 4 XOR 2 = 7.
It can be shown that 7 is the maximum possible bitwise XOR.
Note that other operations may be used to achieve a bitwise XOR of 7.

Example 2:

Input: nums = [1,2,3,9,2]
Output: 11
Explanation: Apply the operation zero times.
The bitwise XOR of all the elements = 1 XOR 2 XOR 3 XOR 9 XOR 2 = 11.
It can be shown that 11 is the maximum possible bitwise XOR.

Constraints:

1 <= nums.length <= 10⁵
0 <= nums[i] <= 10⁸

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    int maximumXOR(vector<int> &nums) {
        int res = 0;

        for (auto &a : nums) {
            res |= a;
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

D

Statement

简体中文English

Metadata

Link: 不同骰子序列的数目
Difficulty: Hard
Tag:

给你一个整数 n 。你需要掷一个 6 面的骰子 n 次。请你在满足以下要求的前提下，求出不同骰子序列的数目：

序列中任意相邻数字的 最大公约数 为 1 。
序列中相等的值之间，至少有 2 个其他值的数字。正式地，如果第 i 次掷骰子的值等于第 j 次的值，那么 abs(i - j) > 2 。

请你返回不同序列的 总数目 。由于答案可能很大，请你将答案对 10⁹ + 7 取余后返回。

如果两个序列中至少有一个元素不同，那么它们被视为不同的序列。

示例 1：

输入：n = 4
输出：184
解释：一些可行的序列为 (1, 2, 3, 4) ，(6, 1, 2, 3) ，(1, 2, 3, 1) 等等。
一些不可行的序列为 (1, 2, 1, 3) ，(1, 2, 3, 6) 。
(1, 2, 1, 3) 是不可行的，因为第一个和第三个骰子值相等且 abs(1 - 3) = 2 （下标从 1 开始表示）。
(1, 2, 3, 6) i是不可行的，因为 3 和 6 的最大公约数是 3 。
总共有 184 个不同的可行序列，所以我们返回 184 。

示例 2：

输入：n = 2
输出：22
解释：一些可行的序列为 (1, 2) ，(2, 1) ，(3, 2) 。
一些不可行的序列为 (3, 6) ，(2, 4) ，因为最大公约数不为 1 。
总共有 22 个不同的可行序列，所以我们返回 22 。

提示：

1 <= n <= 10⁴

Metadata

Link: Number of Distinct Roll Sequences
Difficulty: Hard
Tag:

You are given an integer n. You roll a fair 6-sided dice n times. Determine the total number of distinct sequences of rolls possible such that the following conditions are satisfied:

The greatest common divisor of any adjacent values in the sequence is equal to 1.
There is at least a gap of 2 rolls between equal valued rolls. More formally, if the value of the i^th roll is equal to the value of the j^th roll, then abs(i - j) > 2.

Return the total number of distinct sequences possible. Since the answer may be very large, return it modulo 10⁹ + 7.

Two sequences are considered distinct if at least one element is different.

Example 1:

Input: n = 4
Output: 184
Explanation: Some of the possible sequences are (1, 2, 3, 4), (6, 1, 2, 3), (1, 2, 3, 1), etc.
Some invalid sequences are (1, 2, 1, 3), (1, 2, 3, 6).
(1, 2, 1, 3) is invalid since the first and third roll have an equal value and abs(1 - 3) = 2 (i and j are 1-indexed).
(1, 2, 3, 6) is invalid since the greatest common divisor of 3 and 6 = 3.
There are a total of 184 distinct sequences possible, so we return 184.

Example 2:

Input: n = 2
Output: 22
Explanation: Some of the possible sequences are (1, 2), (2, 1), (3, 2).
Some invalid sequences are (3, 6), (2, 4) since the greatest common divisor is not equal to 1.
There are a total of 22 distinct sequences possible, so we return 22.

Constraints:

1 <= n <= 10⁴

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

const int mod = 1e9 + 7;

// 1 2 1 3
// 1 2 3 6

class Solution {
public:
    int distinctSequences(int n) {
        static auto f = std::invoke([]() {
            auto f = vector<vector<ll>>(1e4 + 5, vector<ll>(10, 0));
            auto g = vector<vector<ll>>(1e4 + 5, vector<ll>(10, 0));

            const int n = 1e4;

            for (int i = 1; i <= 6; i++) {
                f[1][i] = 1;
                g[1][i] = 1;
            }

            for (int i = 2; i <= n; i++) {
                for (int j = 1; j <= 6; j++) {
                    for (int k = 1; k <= 6; k++) {
                        if (j == k || __gcd(j, k) != 1) {
                            continue;
                        }

                        f[i][j] += f[i - 1][k];
                        f[i][j] %= mod;

                        f[i][j] -= g[i - 2][j];
                        f[i][j] += mod;
                        f[i][j] %= mod;

                        if (i >= 3) {
                            f[i][j] += g[i - 3][k];
                            f[i][j] %= mod;
                        }
                    }

                    g[i][j] = f[i][j] + g[i - 2][j];
                    g[i][j] %= mod;
                }
            }

            return f;
        });

        ll res = 0;
        for (int i = 1; i <= 6; i++) {
            res += f[n][i];
            res %= mod;
        }

        return res;

        // return ans[n - 1];

        // static auto f = std::invoke([]() {
        //     auto res = vector<int>(15);

        //     auto dfs = [&res](auto &&dfs, int n, vector<int> &vec) {
        //         if (vec.size() == (size_t)n) {
        //             ++res[n];
        //             return;
        //         }

        //         for (int i = 1; i <= 6; i++) {
        //             if (!vec.empty()) {
        //                 if (vec.back() == i) {
        //                     continue;
        //                 }

        //                 if (__gcd(vec.back(), i) != 1) {
        //                     continue;
        //                 }

        //                 if (vec.size() >= 2 && vec.end()[-2] == i) {
        //                     continue;
        //                 }
        //             }

        //             vec.push_back(i);
        //             dfs(dfs, n, vec);
        //             vec.pop_back();
        //         }
        //     };

        //     for (int i = 1; i <= 15; i++) {
        //         auto tmp = vector<int>();
        //         dfs(dfs, i, tmp);
        //     }

        //     return res;
        // });

        // return f[n];
    }
};

#ifdef LOCAL

int main() {
    auto s = Solution();
    for (int i = 1; i <= 15; i++) {
        cout << s.distinctSequences(i) << ",";
    }

    return 0;
}

#endif

最后更新: October 11, 2023