weekly-contest-308
A
Statement
Metadata
- Link: 和有限的最长子序列
- Difficulty: Easy
- Tag:
给你一个长度为 n 的整数数组 nums ,和一个长度为 m 的整数数组 queries 。
返回一个长度为 m 的数组 answer ,其中 answer[i] 是 nums 中 元素之和小于等于 queries[i] 的 子序列 的 最大 长度 。
子序列 是由一个数组删除某些元素(也可以不删除)但不改变剩余元素顺序得到的一个数组。
示例 1:
输入:nums = [4,5,2,1], queries = [3,10,21]
输出:[2,3,4]
解释:queries 对应的 answer 如下:
- 子序列 [2,1] 的和小于或等于 3 。可以证明满足题目要求的子序列的最大长度是 2 ,所以 answer[0] = 2 。
- 子序列 [4,5,1] 的和小于或等于 10 。可以证明满足题目要求的子序列的最大长度是 3 ,所以 answer[1] = 3 。
- 子序列 [4,5,2,1] 的和小于或等于 21 。可以证明满足题目要求的子序列的最大长度是 4 ,所以 answer[2] = 4 。
示例 2:
输入:nums = [2,3,4,5], queries = [1]
输出:[0]
解释:空子序列是唯一一个满足元素和小于或等于 1 的子序列,所以 answer[0] = 0 。
提示:
n == nums.lengthm == queries.length1 <= n, m <= 10001 <= nums[i], queries[i] <= 106
Metadata
- Link: Longest Subsequence With Limited Sum
- Difficulty: Easy
- Tag:
You are given an integer array nums of length n, and an integer array queries of length m.
Return an array answer of length m where answer[i] is the maximum size of a subsequence that you can take from nums such that the sum of its elements is less than or equal to queries[i].
A subsequence is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
Example 1:
Input: nums = [4,5,2,1], queries = [3,10,21]
Output: [2,3,4]
Explanation: We answer the queries as follows:
- The subsequence [2,1] has a sum less than or equal to 3. It can be proven that 2 is the maximum size of such a subsequence, so answer[0] = 2.
- The subsequence [4,5,1] has a sum less than or equal to 10. It can be proven that 3 is the maximum size of such a subsequence, so answer[1] = 3.
- The subsequence [4,5,2,1] has a sum less than or equal to 21. It can be proven that 4 is the maximum size of such a subsequence, so answer[2] = 4.
Example 2:
Input: nums = [2,3,4,5], queries = [1]
Output: [0]
Explanation: The empty subsequence is the only subsequence that has a sum less than or equal to 1, so answer[0] = 0.
Constraints:
n == nums.lengthm == queries.length1 <= n, m <= 10001 <= nums[i], queries[i] <= 106
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
vector<int> answerQueries(vector<int> &nums, vector<int> &queries) {
int n = int(nums.size());
sort(all(nums));
for (int i = 1; i < n; i++) {
nums[i] += nums[i - 1];
}
auto res = vector<int>();
for (const auto &q : queries) {
auto pos = upper_bound(all(nums), q);
auto x = pos - nums.begin();
res.push_back(int(x));
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 从字符串中移除星号
- Difficulty: Medium
- Tag:
给你一个包含若干星号 * 的字符串 s 。
在一步操作中,你可以:
- 选中
s中的一个星号。 - 移除星号 左侧 最近的那个 非星号 字符,并移除该星号自身。
返回移除 所有 星号之后的字符串。
注意:
- 生成的输入保证总是可以执行题面中描述的操作。
- 可以证明结果字符串是唯一的。
示例 1:
输入:s = "leet**cod*e"
输出:"lecoe"
解释:从左到右执行移除操作:
- 距离第 1 个星号最近的字符是 "leet**cod*e" 中的 't' ,s 变为 "lee*cod*e" 。
- 距离第 2 个星号最近的字符是 "lee*cod*e" 中的 'e' ,s 变为 "lecod*e" 。
- 距离第 3 个星号最近的字符是 "lecod*e" 中的 'd' ,s 变为 "lecoe" 。
不存在其他星号,返回 "lecoe" 。示例 2:
输入:s = "erase*****"
输出:""
解释:整个字符串都会被移除,所以返回空字符串。
提示:
1 <= s.length <= 105s由小写英文字母和星号*组成s可以执行上述操作
Metadata
- Link: Removing Stars From a String
- Difficulty: Medium
- Tag:
You are given a string s, which contains stars *.
In one operation, you can:
- Choose a star in
s. - Remove the closest non-star character to its left, as well as remove the star itself.
Return the string after all stars have been removed.
Note:
- The input will be generated such that the operation is always possible.
- It can be shown that the resulting string will always be unique.
Example 1:
Input: s = "leet**cod*e"
Output: "lecoe"
Explanation: Performing the removals from left to right:
- The closest character to the 1st star is 't' in "leet**cod*e". s becomes "lee*cod*e".
- The closest character to the 2nd star is 'e' in "lee*cod*e". s becomes "lecod*e".
- The closest character to the 3rd star is 'd' in "lecod*e". s becomes "lecoe".
There are no more stars, so we return "lecoe".Example 2:
Input: s = "erase*****"
Output: ""
Explanation: The entire string is removed, so we return an empty string.
Constraints:
1 <= s.length <= 105sconsists of lowercase English letters and stars*.- The operation above can be performed on
s.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
string removeStars(string s) {
std::string res = "";
for (const auto &c : s) {
if (c == '*') {
if (!res.empty()) {
res.pop_back();
continue;
}
}
res += c;
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 收集垃圾的最少总时间
- Difficulty: Medium
- Tag:
给你一个下标从 0 开始的字符串数组 garbage ,其中 garbage[i] 表示第 i 个房子的垃圾集合。garbage[i] 只包含字符 'M' ,'P' 和 'G' ,但可能包含多个相同字符,每个字符分别表示一单位的金属、纸和玻璃。垃圾车收拾 一 单位的任何一种垃圾都需要花费 1 分钟。
同时给你一个下标从 0 开始的整数数组 travel ,其中 travel[i] 是垃圾车从房子 i 行驶到房子 i + 1 需要的分钟数。
城市里总共有三辆垃圾车,分别收拾三种垃圾。每辆垃圾车都从房子 0 出发,按顺序 到达每一栋房子。但它们 不是必须 到达所有的房子。
任何时刻只有 一辆 垃圾车处在使用状态。当一辆垃圾车在行驶或者收拾垃圾的时候,另外两辆车 不能 做任何事情。
请你返回收拾完所有垃圾需要花费的 最少 总分钟数。
示例 1:
输入:garbage = ["G","P","GP","GG"], travel = [2,4,3]
输出:21
解释:
收拾纸的垃圾车:
1. 从房子 0 行驶到房子 1
2. 收拾房子 1 的纸垃圾
3. 从房子 1 行驶到房子 2
4. 收拾房子 2 的纸垃圾
收拾纸的垃圾车总共花费 8 分钟收拾完所有的纸垃圾。
收拾玻璃的垃圾车:
1. 收拾房子 0 的玻璃垃圾
2. 从房子 0 行驶到房子 1
3. 从房子 1 行驶到房子 2
4. 收拾房子 2 的玻璃垃圾
5. 从房子 2 行驶到房子 3
6. 收拾房子 3 的玻璃垃圾
收拾玻璃的垃圾车总共花费 13 分钟收拾完所有的玻璃垃圾。
由于没有金属垃圾,收拾金属的垃圾车不需要花费任何时间。
所以总共花费 8 + 13 = 21 分钟收拾完所有垃圾。
示例 2:
输入:garbage = ["MMM","PGM","GP"], travel = [3,10]
输出:37
解释:
收拾金属的垃圾车花费 7 分钟收拾完所有的金属垃圾。
收拾纸的垃圾车花费 15 分钟收拾完所有的纸垃圾。
收拾玻璃的垃圾车花费 15 分钟收拾完所有的玻璃垃圾。
总共花费 7 + 15 + 15 = 37 分钟收拾完所有的垃圾。
提示:
2 <= garbage.length <= 105garbage[i]只包含字母'M','P'和'G'。1 <= garbage[i].length <= 10travel.length == garbage.length - 11 <= travel[i] <= 100
Metadata
- Link: Minimum Amount of Time to Collect Garbage
- Difficulty: Medium
- Tag:
You are given a 0-indexed array of strings garbage where garbage[i] represents the assortment of garbage at the ith house. garbage[i] consists only of the characters 'M', 'P' and 'G' representing one unit of metal, paper and glass garbage respectively. Picking up one unit of any type of garbage takes 1 minute.
You are also given a 0-indexed integer array travel where travel[i] is the number of minutes needed to go from house i to house i + 1.
There are three garbage trucks in the city, each responsible for picking up one type of garbage. Each garbage truck starts at house 0 and must visit each house in order; however, they do not need to visit every house.
Only one garbage truck may be used at any given moment. While one truck is driving or picking up garbage, the other two trucks cannot do anything.
Return the minimum number of minutes needed to pick up all the garbage.
Example 1:
Input: garbage = ["G","P","GP","GG"], travel = [2,4,3]
Output: 21
Explanation:
The paper garbage truck:
1. Travels from house 0 to house 1
2. Collects the paper garbage at house 1
3. Travels from house 1 to house 2
4. Collects the paper garbage at house 2
Altogether, it takes 8 minutes to pick up all the paper garbage.
The glass garbage truck:
1. Collects the glass garbage at house 0
2. Travels from house 0 to house 1
3. Travels from house 1 to house 2
4. Collects the glass garbage at house 2
5. Travels from house 2 to house 3
6. Collects the glass garbage at house 3
Altogether, it takes 13 minutes to pick up all the glass garbage.
Since there is no metal garbage, we do not need to consider the metal garbage truck.
Therefore, it takes a total of 8 + 13 = 21 minutes to collect all the garbage.
Example 2:
Input: garbage = ["MMM","PGM","GP"], travel = [3,10]
Output: 37
Explanation:
The metal garbage truck takes 7 minutes to pick up all the metal garbage.
The paper garbage truck takes 15 minutes to pick up all the paper garbage.
The glass garbage truck takes 15 minutes to pick up all the glass garbage.
It takes a total of 7 + 15 + 15 = 37 minutes to collect all the garbage.
Constraints:
2 <= garbage.length <= 105garbage[i]consists of only the letters'M','P', and'G'.1 <= garbage[i].length <= 10travel.length == garbage.length - 11 <= travel[i] <= 100
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T& a, const S& b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T& a, const S& b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int garbageCollection(vector<string>& garbage, vector<int>& travel) {
int n = (int)garbage.size();
auto g = vector<vector<int>>(3, vector<int>(n, 0));
for (int i = 0; i < n; i++) {
for (const auto& c : garbage[i]) {
if (c == 'M') {
++g[0][i];
} else if (c == 'P') {
++g[1][i];
} else {
++g[2][i];
}
}
}
auto calc = [&travel](vector<int>& v) -> int {
int res = 0;
while (!v.empty() && v.back() == 0) {
v.pop_back();
}
int m = int(v.size());
for (int i = 0; i < m; i++) {
if (i) {
res += travel[i - 1];
}
res += v[i];
}
return res;
};
int res = 0;
for (int i = 0; i < 3; i++) {
res += calc(g[i]);
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 给定条件下构造矩阵
- Difficulty: Hard
- Tag:
给你一个 正 整数 k ,同时给你:
- 一个大小为
n的二维整数数组rowConditions,其中rowConditions[i] = [abovei, belowi]和 - 一个大小为
m的二维整数数组colConditions,其中colConditions[i] = [lefti, righti]。
两个数组里的整数都是 1 到 k 之间的数字。
你需要构造一个 k x k 的矩阵,1 到 k 每个数字需要 恰好出现一次 。剩余的数字都是 0 。
矩阵还需要满足以下条件:
- 对于所有
0到n - 1之间的下标i,数字abovei所在的 行 必须在数字belowi所在行的上面。 - 对于所有
0到m - 1之间的下标i,数字lefti所在的 列 必须在数字righti所在列的左边。
返回满足上述要求的 任意 矩阵。如果不存在答案,返回一个空的矩阵。
示例 1:
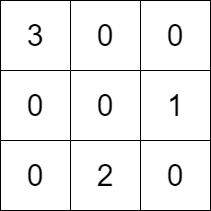
输入:k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]]
输出:[[3,0,0],[0,0,1],[0,2,0]]
解释:上图为一个符合所有条件的矩阵。
行要求如下:
- 数字 1 在第 1 行,数字 2 在第 2 行,1 在 2 的上面。
- 数字 3 在第 0 行,数字 2 在第 2 行,3 在 2 的上面。
列要求如下:
- 数字 2 在第 1 列,数字 1 在第 2 列,2 在 1 的左边。
- 数字 3 在第 0 列,数字 2 在第 1 列,3 在 2 的左边。
注意,可能有多种正确的答案。
示例 2:
输入:k = 3, rowConditions = [[1,2],[2,3],[3,1],[2,3]], colConditions = [[2,1]]
输出:[]
解释:由前两个条件可以得到 3 在 1 的下面,但第三个条件是 3 在 1 的上面。
没有符合条件的矩阵存在,所以我们返回空矩阵。
提示:
2 <= k <= 4001 <= rowConditions.length, colConditions.length <= 104rowConditions[i].length == colConditions[i].length == 21 <= abovei, belowi, lefti, righti <= kabovei != belowilefti != righti
Metadata
- Link: Build a Matrix With Conditions
- Difficulty: Hard
- Tag:
You are given a positive integer k. You are also given:
- a 2D integer array
rowConditionsof sizenwhererowConditions[i] = [abovei, belowi], and - a 2D integer array
colConditionsof sizemwherecolConditions[i] = [lefti, righti].
The two arrays contain integers from 1 to k.
You have to build a k x k matrix that contains each of the numbers from 1 to k exactly once. The remaining cells should have the value 0.
The matrix should also satisfy the following conditions:
- The number
aboveishould appear in a row that is strictly above the row at which the numberbelowiappears for allifrom0ton - 1. - The number
leftishould appear in a column that is strictly left of the column at which the numberrightiappears for allifrom0tom - 1.
Return any matrix that satisfies the conditions. If no answer exists, return an empty matrix.
Example 1:

Input: k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]]
Output: [[3,0,0],[0,0,1],[0,2,0]]
Explanation: The diagram above shows a valid example of a matrix that satisfies all the conditions.
The row conditions are the following:
- Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix.
- Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix.
The column conditions are the following:
- Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix.
- Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix.
Note that there may be multiple correct answers.
Example 2:
Input: k = 3, rowConditions = [[1,2],[2,3],[3,1],[2,3]], colConditions = [[2,1]]
Output: []
Explanation: From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied.
No matrix can satisfy all the conditions, so we return the empty matrix.
Constraints:
2 <= k <= 4001 <= rowConditions.length, colConditions.length <= 104rowConditions[i].length == colConditions[i].length == 21 <= abovei, belowi, lefti, righti <= kabovei != belowilefti != righti
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
vector<vector<int>> buildMatrix(int k, vector<vector<int>> &rowConditions, vector<vector<int>> &colConditions) {
auto calc = [&k](const vector<vector<int>> &vec) {
auto g = vector<vector<int>>(k + 1, vector<int>());
auto d = vector<int>(k + 1, 0);
for (const auto &v : vec) {
g[v[0]].push_back(v[1]);
++d[v[1]];
}
vector<int> ordered, unordered;
for (int i = 1; i <= k; i++) {
if (d[i] == 0) {
unordered.push_back(i);
}
}
while (!unordered.empty()) {
int u = unordered.back();
unordered.pop_back();
ordered.push_back(u);
for (int v : g[u]) {
if (--d[v] == 0) {
unordered.push_back(v);
}
}
}
if (int(ordered.size()) != k) {
return vector<int>();
}
auto res = vector<int>(k, 0);
for (int i = 0; i < k; i++) {
res[ordered[i] - 1] = i;
}
return res;
};
auto f = calc(rowConditions);
auto g = calc(colConditions);
if (f.empty() || g.empty()) {
return vector<vector<int>>();
}
auto res = vector<vector<int>>(k, vector<int>(k, 0));
for (int i = 0; i < k; i++) {
res[f[i]][g[i]] = i + 1;
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif