biweekly-contest-93
A
Statement
Metadata
- Link: 数组中字符串的最大值
- Difficulty: Easy
- Tag:
一个由字母和数字组成的字符串的 值 定义如下:
- 如果字符串 只 包含数字,那么值为该字符串在
10进制下的所表示的数字。 - 否则,值为字符串的 长度 。
给你一个字符串数组 strs ,每个字符串都只由字母和数字组成,请你返回 strs 中字符串的 最大值 。
示例 1:
输入:strs = ["alic3","bob","3","4","00000"]
输出:5
解释:
- "alic3" 包含字母和数字,所以值为长度 5 。
- "bob" 只包含字母,所以值为长度 3 。
- "3" 只包含数字,所以值为 3 。
- "4" 只包含数字,所以值为 4 。
- "00000" 只包含数字,所以值为 0 。
所以最大的值为 5 ,是字符串 "alic3" 的值。
示例 2:
输入:strs = ["1","01","001","0001"]
输出:1
解释:
数组中所有字符串的值都是 1 ,所以我们返回 1 。
提示:
1 <= strs.length <= 1001 <= strs[i].length <= 9strs[i]只包含小写英文字母和数字。
Metadata
- Link: Maximum Value of a String in an Array
- Difficulty: Easy
- Tag:
The value of an alphanumeric string can be defined as:
- The numeric representation of the string in base
10, if it comprises of digits only. - The length of the string, otherwise.
Given an array strs of alphanumeric strings, return the maximum value of any string in strs.
Example 1:
Input: strs = ["alic3","bob","3","4","00000"]
Output: 5
Explanation:
- "alic3" consists of both letters and digits, so its value is its length, i.e. 5.
- "bob" consists only of letters, so its value is also its length, i.e. 3.
- "3" consists only of digits, so its value is its numeric equivalent, i.e. 3.
- "4" also consists only of digits, so its value is 4.
- "00000" consists only of digits, so its value is 0.
Hence, the maximum value is 5, of "alic3".
Example 2:
Input: strs = ["1","01","001","0001"]
Output: 1
Explanation:
Each string in the array has value 1. Hence, we return 1.
Constraints:
1 <= strs.length <= 1001 <= strs[i].length <= 9strs[i]consists of only lowercase English letters and digits.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int maximumValue(vector<string> &strs) {
ll res = 0;
for (const auto &s : strs) {
ll cur = 0;
for (const auto &c : s) {
if (c >= '0' && c <= '9') {
cur = cur * 10 + (c - '0');
} else {
cur = ll(s.length());
break;
}
}
res = max(res, cur);
}
return int(res);
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 图中最大星和
- Difficulty: Medium
- Tag:
给你一个 n 个点的无向图,节点从 0 到 n - 1 编号。给你一个长度为 n 下标从 0 开始的整数数组 vals ,其中 vals[i] 表示第 i 个节点的值。
同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条双向边。
星图 是给定图中的一个子图,它包含一个中心节点和 0 个或更多个邻居。换言之,星图是给定图中一个边的子集,且这些边都有一个公共节点。
下图分别展示了有 3 个和 4 个邻居的星图,蓝色节点为中心节点。
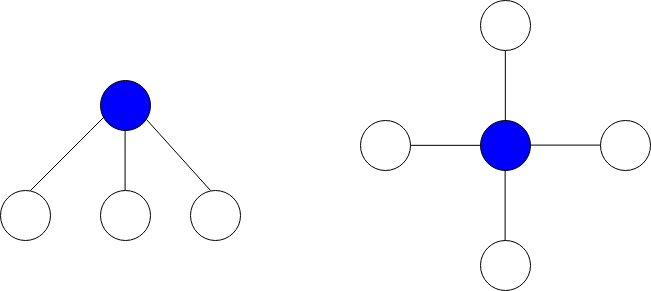
星和 定义为星图中所有节点值的和。
给你一个整数 k ,请你返回 至多 包含 k 条边的星图中的 最大星和 。
示例 1:
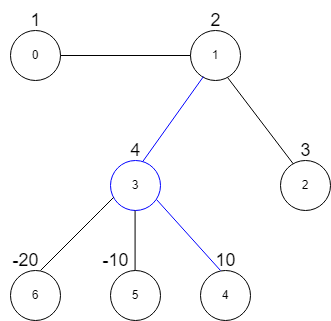
输入:vals = [1,2,3,4,10,-10,-20], edges = [[0,1],[1,2],[1,3],[3,4],[3,5],[3,6]], k = 2
输出:16
解释:上图展示了输入示例。
最大星和对应的星图在上图中用蓝色标出。中心节点是 3 ,星图中还包含邻居 1 和 4 。
无法得到一个和大于 16 且边数不超过 2 的星图。
示例 2:
输入:vals = [-5], edges = [], k = 0
输出:-5
解释:只有一个星图,就是节点 0 自己。
所以我们返回 -5 。
提示:
n == vals.length1 <= n <= 105-104 <= vals[i] <= 1040 <= edges.length <= min(n * (n - 1) / 2, 105)edges[i].length == 20 <= ai, bi <= n - 1ai != bi0 <= k <= n - 1
Metadata
- Link: Maximum Star Sum of a Graph
- Difficulty: Medium
- Tag:
There is an undirected graph consisting of n nodes numbered from 0 to n - 1. You are given a 0-indexed integer array vals of length n where vals[i] denotes the value of the ith node.
You are also given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.
A star graph is a subgraph of the given graph having a center node containing 0 or more neighbors. In other words, it is a subset of edges of the given graph such that there exists a common node for all edges.
The image below shows star graphs with 3 and 4 neighbors respectively, centered at the blue node.

The star sum is the sum of the values of all the nodes present in the star graph.
Given an integer k, return the maximum star sum of a star graph containing at most k edges.
Example 1:

Input: vals = [1,2,3,4,10,-10,-20], edges = [[0,1],[1,2],[1,3],[3,4],[3,5],[3,6]], k = 2
Output: 16
Explanation: The above diagram represents the input graph.
The star graph with the maximum star sum is denoted by blue. It is centered at 3 and includes its neighbors 1 and 4.
It can be shown it is not possible to get a star graph with a sum greater than 16.
Example 2:
Input: vals = [-5], edges = [], k = 0
Output: -5
Explanation: There is only one possible star graph, which is node 0 itself.
Hence, we return -5.
Constraints:
n == vals.length1 <= n <= 105-104 <= vals[i] <= 1040 <= edges.length <= min(n * (n - 1) / 2, 105)edges[i].length == 20 <= ai, bi <= n - 1ai != bi0 <= k <= n - 1
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int maxStarSum(vector<int> &vals, vector<vector<int>> &edges, int k) {
int n = int(vals.size());
auto f = vector<vector<int>>(n + 5, vector<int>());
for (const auto &e : edges) {
int u = e[0];
int v = e[1];
f[u].push_back(vals[v]);
f[v].push_back(vals[u]);
}
int res = -0x3f3f3f3f;
for (int i = 0; i < n; i++) {
sort(all(f[i]));
reverse(all(f[i]));
int cur = vals[i];
for (int j = 0; j < min(k, int(f[i].size())); j++) {
if (f[i][j] <= 0) {
break;
}
cur += f[i][j];
}
res = max(res, cur);
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 青蛙过河 II
- Difficulty: Medium
- Tag:
给你一个下标从 0 开始的整数数组 stones ,数组中的元素 严格递增 ,表示一条河中石头的位置。
一只青蛙一开始在第一块石头上,它想到达最后一块石头,然后回到第一块石头。同时每块石头 至多 到达 一次。
一次跳跃的 长度 是青蛙跳跃前和跳跃后所在两块石头之间的距离。
- 更正式的,如果青蛙从
stones[i]跳到stones[j],跳跃的长度为|stones[i] - stones[j]|。
一条路径的 代价 是这条路径里的 最大跳跃长度 。
请你返回这只青蛙的 最小代价 。
示例 1:
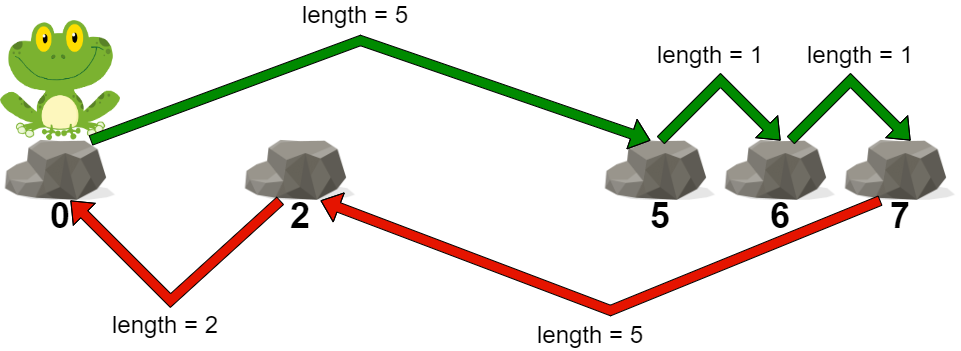
输入:stones = [0,2,5,6,7]
输出:5
解释:上图展示了一条最优路径。
这条路径的代价是 5 ,是这条路径中的最大跳跃长度。
无法得到一条代价小于 5 的路径,我们返回 5 。
示例 2:

输入:stones = [0,3,9]
输出:9
解释:
青蛙可以直接跳到最后一块石头,然后跳回第一块石头。
在这条路径中,每次跳跃长度都是 9 。所以路径代价是 max(9, 9) = 9 。
这是可行路径中的最小代价。
提示:
2 <= stones.length <= 1050 <= stones[i] <= 109stones[0] == 0stones中的元素严格递增。
Metadata
- Link: Frog Jump II
- Difficulty: Medium
- Tag:
You are given a 0-indexed integer array stones sorted in strictly increasing order representing the positions of stones in a river.
A frog, initially on the first stone, wants to travel to the last stone and then return to the first stone. However, it can jump to any stone at most once.
The length of a jump is the absolute difference between the position of the stone the frog is currently on and the position of the stone to which the frog jumps.
- More formally, if the frog is at
stones[i]and is jumping tostones[j], the length of the jump is|stones[i] - stones[j]|.
The cost of a path is the maximum length of a jump among all jumps in the path.
Return the minimum cost of a path for the frog.
Example 1:

Input: stones = [0,2,5,6,7]
Output: 5
Explanation: The above figure represents one of the optimal paths the frog can take.
The cost of this path is 5, which is the maximum length of a jump.
Since it is not possible to achieve a cost of less than 5, we return it.
Example 2:

Input: stones = [0,3,9]
Output: 9
Explanation:
The frog can jump directly to the last stone and come back to the first stone.
In this case, the length of each jump will be 9. The cost for the path will be max(9, 9) = 9.
It can be shown that this is the minimum achievable cost.
Constraints:
2 <= stones.length <= 1050 <= stones[i] <= 109stones[0] == 0stonesis sorted in a strictly increasing order.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int maxJump(vector<int> &stones) {
int n = int(stones.size());
int l = 0, r = abs(stones.end()[-1] - stones[0]), res = -1;
const auto check = [&](int x) -> bool {
auto vis = vector<int>(n + 5, 0);
int pre_ix = 0;
for (int i = 1; i < n; i++) {
if (abs(stones[pre_ix] - stones[i]) > x) {
if (i - 1 == pre_ix) {
return false;
}
vis[i - 1] = true;
pre_ix = i - 1;
}
}
if (stones[n - 1] - stones[pre_ix] > x) {
return false;
}
pre_ix = 0;
for (int i = 1; i < n; i++) {
if (!vis[i]) {
if (stones[i] - stones[pre_ix] > x) {
return false;
}
pre_ix = i;
}
}
if (stones[n - 1] - stones[pre_ix] > x) {
return false;
}
return true;
};
while (r - l >= 0) {
int mid = (l + r) >> 1;
if (check(mid)) {
r = mid - 1;
res = mid;
} else {
l = mid + 1;
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 让数组不相等的最小总代价
- Difficulty: Hard
- Tag:
给你两个下标从 0 开始的整数数组 nums1 和 nums2 ,两者长度都为 n 。
每次操作中,你可以选择交换 nums1 中任意两个下标处的值。操作的 开销 为两个下标的 和 。
你的目标是对于所有的 0 <= i <= n - 1 ,都满足 nums1[i] != nums2[i] ,你可以进行 任意次 操作,请你返回达到这个目标的 最小 总代价。
请你返回让 nums1 和 nums2 满足上述条件的 最小总代价 ,如果无法达成目标,返回 -1 。
示例 1:
输入:nums1 = [1,2,3,4,5], nums2 = [1,2,3,4,5]
输出:10
解释:
实现目标的其中一种方法为:
- 交换下标为 0 和 3 的两个值,代价为 0 + 3 = 3 。现在 nums1 = [4,2,3,1,5] 。
- 交换下标为 1 和 2 的两个值,代价为 1 + 2 = 3 。现在 nums1 = [4,3,2,1,5] 。
- 交换下标为 0 和 4 的两个值,代价为 0 + 4 = 4 。现在 nums1 = [5,3,2,1,4] 。
最后,对于每个下标 i ,都有 nums1[i] != nums2[i] 。总代价为 10 。
还有别的交换值的方法,但是无法得到代价和小于 10 的方案。
示例 2:
输入:nums1 = [2,2,2,1,3], nums2 = [1,2,2,3,3]
输出:10
解释:
实现目标的一种方法为:
- 交换下标为 2 和 3 的两个值,代价为 2 + 3 = 5 。现在 nums1 = [2,2,1,2,3] 。
- 交换下标为 1 和 4 的两个值,代价为 1 + 4 = 5 。现在 nums1 = [2,3,1,2,2] 。
总代价为 10 ,是所有方案中的最小代价。
示例 3:
输入:nums1 = [1,2,2], nums2 = [1,2,2]
输出:-1
解释:
不管怎么操作,都无法满足题目要求。
所以返回 -1 。
提示:
n == nums1.length == nums2.length1 <= n <= 1051 <= nums1[i], nums2[i] <= n
Metadata
- Link: Minimum Total Cost to Make Arrays Unequal
- Difficulty: Hard
- Tag:
You are given two 0-indexed integer arrays nums1 and nums2, of equal length n.
In one operation, you can swap the values of any two indices of nums1. The cost of this operation is the sum of the indices.
Find the minimum total cost of performing the given operation any number of times such that nums1[i] != nums2[i] for all 0 <= i <= n - 1 after performing all the operations.
Return the minimum total cost such that nums1 and nums2 satisfy the above condition. In case it is not possible, return -1.
Example 1:
Input: nums1 = [1,2,3,4,5], nums2 = [1,2,3,4,5]
Output: 10
Explanation:
One of the ways we can perform the operations is:
- Swap values at indices 0 and 3, incurring cost = 0 + 3 = 3. Now, nums1 = [4,2,3,1,5]
- Swap values at indices 1 and 2, incurring cost = 1 + 2 = 3. Now, nums1 = [4,3,2,1,5].
- Swap values at indices 0 and 4, incurring cost = 0 + 4 = 4. Now, nums1 =[5,3,2,1,4].
We can see that for each index i, nums1[i] != nums2[i]. The cost required here is 10.
Note that there are other ways to swap values, but it can be proven that it is not possible to obtain a cost less than 10.
Example 2:
Input: nums1 = [2,2,2,1,3], nums2 = [1,2,2,3,3]
Output: 10
Explanation:
One of the ways we can perform the operations is:
- Swap values at indices 2 and 3, incurring cost = 2 + 3 = 5. Now, nums1 = [2,2,1,2,3].
- Swap values at indices 1 and 4, incurring cost = 1 + 4 = 5. Now, nums1 = [2,3,1,2,2].
The total cost needed here is 10, which is the minimum possible.
Example 3:
Input: nums1 = [1,2,2], nums2 = [1,2,2]
Output: -1
Explanation:
It can be shown that it is not possible to satisfy the given conditions irrespective of the number of operations we perform.
Hence, we return -1.
Constraints:
n == nums1.length == nums2.length1 <= n <= 1051 <= nums1[i], nums2[i] <= n
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
long long minimumTotalCost(vector<int> &nums1, vector<int> &nums2) {
int n = int(nums1.size());
ll res = 0;
int swap_cnt = 0, mode = 0, mode_cnt = 0;
auto cnt = vector<int>(n + 5, 0);
for (int i = 0; i < n; i++) {
int x = nums1[i];
int y = nums2[i];
if (x == y) {
res += i;
++swap_cnt;
++cnt[x];
if (cnt[x] > mode_cnt) {
mode = x;
mode_cnt = cnt[x];
}
}
}
for (int i = 0; i < n && mode_cnt * 2 > swap_cnt; i++) {
int x = nums1[i];
int y = nums2[i];
if (x != y && x != mode && y != mode) {
res += i;
++swap_cnt;
}
}
if (mode_cnt * 2 > swap_cnt) {
return -1;
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif