weekly-contest-205
A
Statement
Metadata
- Link: 替换所有的问号
- Difficulty: Easy
- Tag:
字符串
给你一个仅包含小写英文字母和 '?' 字符的字符串 s,请你将所有的 '?' 转换为若干小写字母,使最终的字符串不包含任何 连续重复 的字符。
注意:你 不能 修改非 '?' 字符。
题目测试用例保证 除 '?' 字符 之外,不存在连续重复的字符。
在完成所有转换(可能无需转换)后返回最终的字符串。如果有多个解决方案,请返回其中任何一个。可以证明,在给定的约束条件下,答案总是存在的。
示例 1:
输入:s = "?zs"
输出:"azs"
解释:该示例共有 25 种解决方案,从 "azs" 到 "yzs" 都是符合题目要求的。只有 "z" 是无效的修改,因为字符串 "zzs" 中有连续重复的两个 'z' 。示例 2:
输入:s = "ubv?w"
输出:"ubvaw"
解释:该示例共有 24 种解决方案,只有替换成 "v" 和 "w" 不符合题目要求。因为 "ubvvw" 和 "ubvww" 都包含连续重复的字符。
示例 3:
输入:s = "j?qg??b"
输出:"jaqgacb"
示例 4:
输入:s = "??yw?ipkj?"
输出:"acywaipkja"
提示:
-
1 <= s.length <= 100 -
s仅包含小写英文字母和'?'字符
Metadata
- Link: Replace All ?'s to Avoid Consecutive Repeating Characters
- Difficulty: Easy
- Tag:
String
Given a string s containing only lowercase English letters and the '?' character, convert all the '?' characters into lowercase letters such that the final string does not contain any consecutive repeating characters. You cannot modify the non '?' characters.
It is guaranteed that there are no consecutive repeating characters in the given string except for '?'.
Return the final string after all the conversions (possibly zero) have been made. If there is more than one solution, return any of them. It can be shown that an answer is always possible with the given constraints.
Example 1:
Input: s = "?zs"
Output: "azs"
Explanation: There are 25 solutions for this problem. From "azs" to "yzs", all are valid. Only "z" is an invalid modification as the string will consist of consecutive repeating characters in "zzs".
Example 2:
Input: s = "ubv?w"
Output: "ubvaw"
Explanation: There are 24 solutions for this problem. Only "v" and "w" are invalid modifications as the strings will consist of consecutive repeating characters in "ubvvw" and "ubvww".
Constraints:
1 <= s.length <= 100sconsist of lowercase English letters and'?'.
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n;
class Solution {
public:
string modifyString(string s) {
n = SZ(s);
for (int i = 0; i < n; ++i) {
if (s[i] == '?') {
for (int j = 0; j < 26; ++j) {
if (i && j == s[i - 1] - 'a')
continue;
if (i < n - 1 && j == s[i + 1] - 'a')
continue;
s[i] = j + 'a';
}
}
}
return s;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 数的平方等于两数乘积的方法数
- Difficulty: Medium
- Tag:
数组哈希表数学双指针
给你两个整数数组 nums1 和 nums2 ,请你返回根据以下规则形成的三元组的数目(类型 1 和类型 2 ):
- 类型 1:三元组
(i, j, k),如果nums1[i]2 == nums2[j] * nums2[k]其中0 <= i < nums1.length且0 <= j < k < nums2.length - 类型 2:三元组
(i, j, k),如果nums2[i]2 == nums1[j] * nums1[k]其中0 <= i < nums2.length且0 <= j < k < nums1.length
示例 1:
输入:nums1 = [7,4], nums2 = [5,2,8,9]
输出:1
解释:类型 1:(1,1,2), nums1[1]^2 = nums2[1] * nums2[2] (4^2 = 2 * 8)示例 2:
输入:nums1 = [1,1], nums2 = [1,1,1]
输出:9
解释:所有三元组都符合题目要求,因为 1^2 = 1 * 1
类型 1:(0,0,1), (0,0,2), (0,1,2), (1,0,1), (1,0,2), (1,1,2), nums1[i]^2 = nums2[j] * nums2[k]
类型 2:(0,0,1), (1,0,1), (2,0,1), nums2[i]^2 = nums1[j] * nums1[k]
示例 3:
输入:nums1 = [7,7,8,3], nums2 = [1,2,9,7]
输出:2
解释:有两个符合题目要求的三元组
类型 1:(3,0,2), nums1[3]^2 = nums2[0] * nums2[2]
类型 2:(3,0,1), nums2[3]^2 = nums1[0] * nums1[1]
示例 4:
输入:nums1 = [4,7,9,11,23], nums2 = [3,5,1024,12,18]
输出:0
解释:不存在符合题目要求的三元组
提示:
1 <= nums1.length, nums2.length <= 10001 <= nums1[i], nums2[i] <= 10^5
Metadata
- Link: Number of Ways Where Square of Number Is Equal to Product of Two Numbers
- Difficulty: Medium
- Tag:
ArrayHash TableMathTwo Pointers
Given two arrays of integers nums1 and nums2, return the number of triplets formed (type 1 and type 2) under the following rules:
- Type 1: Triplet (i, j, k) if
nums1[i]2 == nums2[j] * nums2[k]where0 <= i < nums1.lengthand0 <= j < k < nums2.length. - Type 2: Triplet (i, j, k) if
nums2[i]2 == nums1[j] * nums1[k]where0 <= i < nums2.lengthand0 <= j < k < nums1.length.
Example 1:
Input: nums1 = [7,4], nums2 = [5,2,8,9]
Output: 1
Explanation: Type 1: (1, 1, 2), nums1[1]2 = nums2[1] * nums2[2]. (42 = 2 * 8).
Example 2:
Input: nums1 = [1,1], nums2 = [1,1,1]
Output: 9
Explanation: All Triplets are valid, because 12 = 1 * 1.
Type 1: (0,0,1), (0,0,2), (0,1,2), (1,0,1), (1,0,2), (1,1,2). nums1[i]2 = nums2[j] * nums2[k].
Type 2: (0,0,1), (1,0,1), (2,0,1). nums2[i]2 = nums1[j] * nums1[k].
Example 3:
Input: nums1 = [7,7,8,3], nums2 = [1,2,9,7]
Output: 2
Explanation: There are 2 valid triplets.
Type 1: (3,0,2). nums1[3]2 = nums2[0] * nums2[2].
Type 2: (3,0,1). nums2[3]2 = nums1[0] * nums1[1].
Constraints:
1 <= nums1.length, nums2.length <= 10001 <= nums1[i], nums2[i] <= 105
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n;
int cnt[N];
int sqr(ll x) {
int y = sqrt(x);
for (int i = max(1, y - 5); i <= y + 5; ++i) {
if (1ll * i * i == x)
return i;
}
return 0;
}
int gao(vector<int> nums1, vector<int> nums2) {
memset(cnt, 0, sizeof cnt);
for (auto &it : nums1) ++cnt[it];
int res = 0;
int n = SZ(nums2);
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
res += cnt[sqr(1ll * nums2[i] * nums2[j])];
}
}
return res;
}
class Solution {
public:
int numTriplets(vector<int> &nums1, vector<int> &nums2) {
int res = gao(nums1, nums2) + gao(nums2, nums1);
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 使绳子变成彩色的最短时间
- Difficulty: Medium
- Tag:
贪心数组字符串动态规划
Alice 把 n 个气球排列在一根绳子上。给你一个下标从 0 开始的字符串 colors ,其中 colors[i] 是第 i 个气球的颜色。
Alice 想要把绳子装扮成 彩色 ,且她不希望两个连续的气球涂着相同的颜色,所以她喊来 Bob 帮忙。Bob 可以从绳子上移除一些气球使绳子变成 彩色 。给你一个下标从 0 开始的整数数组 neededTime ,其中 neededTime[i] 是 Bob 从绳子上移除第 i 个气球需要的时间(以秒为单位)。
返回 Bob 使绳子变成 彩色 需要的 最少时间 。
示例 1:
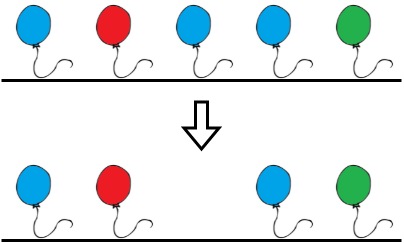
输入:colors = "abaac", neededTime = [1,2,3,4,5]
输出:3
解释:在上图中,'a' 是蓝色,'b' 是红色且 'c' 是绿色。
Bob 可以移除下标 2 的蓝色气球。这将花费 3 秒。
移除后,不存在两个连续的气球涂着相同的颜色。总时间 = 3 。示例 2:
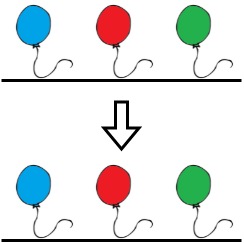
输入:colors = "abc", neededTime = [1,2,3]
输出:0
解释:绳子已经是彩色的,Bob 不需要从绳子上移除任何气球。
示例 3:
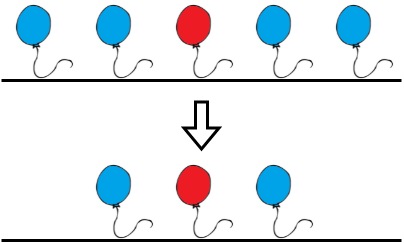
输入:colors = "aabaa", neededTime = [1,2,3,4,1]
输出:2
解释:Bob 会移除下标 0 和下标 4 处的气球。这两个气球各需要 1 秒来移除。
移除后,不存在两个连续的气球涂着相同的颜色。总时间 = 1 + 1 = 2 。
提示:
n == colors.length == neededTime.length1 <= n <= 1051 <= neededTime[i] <= 104colors仅由小写英文字母组成
Metadata
- Link: Minimum Time to Make Rope Colorful
- Difficulty: Medium
- Tag:
GreedyArrayStringDynamic Programming
Alice has n balloons arranged on a rope. You are given a 0-indexed string colors where colors[i] is the color of the ith balloon.
Alice wants the rope to be colorful. She does not want two consecutive balloons to be of the same color, so she asks Bob for help. Bob can remove some balloons from the rope to make it colorful. You are given a 0-indexed integer array neededTime where neededTime[i] is the time (in seconds) that Bob needs to remove the ith balloon from the rope.
Return the minimum time Bob needs to make the rope colorful.
Example 1:

Input: colors = "abaac", neededTime = [1,2,3,4,5]
Output: 3
Explanation: In the above image, 'a' is blue, 'b' is red, and 'c' is green.
Bob can remove the blue balloon at index 2. This takes 3 seconds.
There are no longer two consecutive balloons of the same color. Total time = 3.Example 2:

Input: colors = "abc", neededTime = [1,2,3]
Output: 0
Explanation: The rope is already colorful. Bob does not need to remove any balloons from the rope.
Example 3:

Input: colors = "aabaa", neededTime = [1,2,3,4,1]
Output: 2
Explanation: Bob will remove the ballons at indices 0 and 4. Each ballon takes 1 second to remove.
There are no longer two consecutive balloons of the same color. Total time = 1 + 1 = 2.
Constraints:
n == colors.length == neededTime.length1 <= n <= 1051 <= neededTime[i] <= 104colorscontains only lowercase English letters.
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n;
int f[N][30];
class Solution {
public:
int minCost(string s, vector<int> &cost) {
n = SZ(s);
memset(f, 0x3f, sizeof f);
memset(f[0], 0, sizeof f[0]);
for (int i = 1; i <= n; ++i) {
int ch = s[i - 1] - 'a';
int fee = cost[i - 1];
for (int j = 0; j < 26; ++j) {
if (j != ch) {
chmin(f[i][ch], f[i - 1][j]);
chmin(f[i][j], f[i - 1][j] + fee);
} else {
chmin(f[i][j], f[i - 1][j] + fee);
}
}
}
int res = 2e9;
for (int i = 0; i < 26; ++i) chmin(res, f[n][i]);
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 保证图可完全遍历
- Difficulty: Hard
- Tag:
并查集图
Alice 和 Bob 共有一个无向图,其中包含 n 个节点和 3 种类型的边:
- 类型 1:只能由 Alice 遍历。
- 类型 2:只能由 Bob 遍历。
- 类型 3:Alice 和 Bob 都可以遍历。
给你一个数组 edges ,其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下,找出可以删除的最大边数。如果从任何节点开始,Alice 和 Bob 都可以到达所有其他节点,则认为图是可以完全遍历的。
返回可以删除的最大边数,如果 Alice 和 Bob 无法完全遍历图,则返回 -1 。
示例 1:
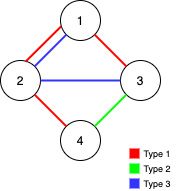
输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
输出:2
解释:如果删除 [1,1,2] 和 [1,1,3] 这两条边,Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。
示例 2:
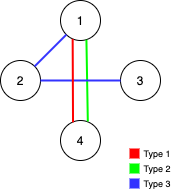
输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
输出:0
解释:注意,删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。
示例 3:
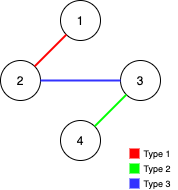
输入:n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
输出:-1
解释:在当前图中,Alice 无法从其他节点到达节点 4 。类似地,Bob 也不能达到节点 1 。因此,图无法完全遍历。
提示:
1 <= n <= 10^51 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)edges[i].length == 31 <= edges[i][0] <= 31 <= edges[i][1] < edges[i][2] <= n- 所有元组
(typei, ui, vi)互不相同
Metadata
- Link: Remove Max Number of Edges to Keep Graph Fully Traversable
- Difficulty: Hard
- Tag:
Union FindGraph
Alice and Bob have an undirected graph of n nodes and 3 types of edges:
- Type 1: Can be traversed by Alice only.
- Type 2: Can be traversed by Bob only.
- Type 3: Can by traversed by both Alice and Bob.
Given an array edges where edges[i] = [typei, ui, vi] represents a bidirectional edge of type typei between nodes ui and vi, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.
Return the maximum number of edges you can remove, or return -1 if it's impossible for the graph to be fully traversed by Alice and Bob.
Example 1:
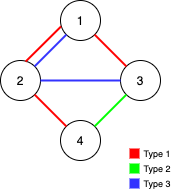
Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
Output: 2
Explanation: If we remove the 2 edges [1,1,2] and [1,1,3]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.
Example 2:
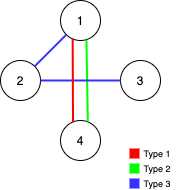
Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
Output: 0
Explanation: Notice that removing any edge will not make the graph fully traversable by Alice and Bob.
Example 3:
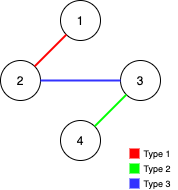
Input: n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
Output: -1
Explanation: In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.
Constraints:
1 <= n <= 10^51 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)edges[i].length == 31 <= edges[i][0] <= 31 <= edges[i][1] < edges[i][2] <= n- All tuples
(typei, ui, vi)are distinct.
Solution
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
x += y;
while (x >= Mod) x -= Mod;
while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
if (x < y)
x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
if (x > y)
x = y;
}
inline int nextInt() {
int x;
cin >> x;
return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
cin >> arg;
rd(args...);
}
#define dbg(x...) \
do { \
cout << "\033[32;1m" << #x << " -> "; \
err(x); \
} while (0)
void err() {
cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
cout << arg << ' ';
err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
for (auto &v : arg) cout << v << ' ';
err(args...);
}
void ptt() {
cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
cout << ' ' << arg;
ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
cout << arg;
ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
pt(args...);
}
inline ll qpow(ll base, ll n) {
assert(n >= 0);
ll res = 1;
while (n) {
if (n & 1)
res = res * base % mod;
base = base * base % mod;
n >>= 1;
}
return res;
}
// head
constexpr int N = 1e5 + 10;
int n;
vector<vector<int>> edges;
struct UFS {
int fa[N], rk[N];
void init(int n) {
memset(fa, 0, sizeof(fa[0]) * (n + 5));
memset(rk, 0, sizeof(rk[0]) * (n + 5));
}
int find(int x) {
return fa[x] == 0 ? x : fa[x] = find(fa[x]);
}
bool merge(int x, int y) {
int fx = find(x), fy = find(y);
if (fx != fy) {
if (rk[fx] > rk[fy])
swap(fx, fy);
fa[fx] = fy;
if (rk[fx] == rk[fy])
++rk[fy];
return true;
}
return false;
}
bool same(int x, int y) {
return find(x) == find(y);
}
} ufs[3];
int gao() {
ufs[0].init(n);
ufs[1].init(n);
ufs[2].init(n);
int res = 0;
for (auto &it : edges) {
int tp = it[0], u = it[1], v = it[2];
if (tp == 3) {
res += ufs[0].merge(u, v) ^ 1;
}
}
ufs[1] = ufs[2] = ufs[0];
for (int i = 1; i <= 2; ++i) {
for (auto &it : edges) {
int tp = it[0], u = it[1], v = it[2];
if (tp == i) {
res += ufs[i].merge(u, v) ^ 1;
}
}
int cnt = 0;
for (int j = 1; j <= n; ++j) {
cnt += ufs[i].fa[j] == 0;
}
if (cnt > 1)
return -1;
}
return res;
}
class Solution {
public:
int maxNumEdgesToRemove(int _n, vector<vector<int>> &_edges) {
n = _n;
edges = _edges;
return gao();
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif