weekly-contest-311
A
Statement
Metadata
- Link: 最小偶倍数
- Difficulty: Easy
- Tag:
给你一个正整数 n ,返回 2 和 n 的最小公倍数(正整数)。
示例 1:
输入:n = 5
输出:10
解释:5 和 2 的最小公倍数是 10 。
示例 2:
输入:n = 6
输出:6
解释:6 和 2 的最小公倍数是 6 。注意数字会是它自身的倍数。
提示:
1 <= n <= 150
Metadata
- Link: Smallest Even Multiple
- Difficulty: Easy
- Tag:
Given a positive integer n, return the smallest positive integer that is a multiple of both 2 and n.
Example 1:
Input: n = 5
Output: 10
Explanation: The smallest multiple of both 5 and 2 is 10.
Example 2:
Input: n = 6
Output: 6
Explanation: The smallest multiple of both 6 and 2 is 6. Note that a number is a multiple of itself.
Constraints:
1 <= n <= 150
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int smallestEvenMultiple(int n) {
return n * 2 / __gcd(n, 2);
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 最长的字母序连续子字符串的长度
- Difficulty: Medium
- Tag:
字母序连续字符串 是由字母表中连续字母组成的字符串。换句话说,字符串 "abcdefghijklmnopqrstuvwxyz" 的任意子字符串都是 字母序连续字符串 。
- 例如,
"abc"是一个字母序连续字符串,而"acb"和"za"不是。
给你一个仅由小写英文字母组成的字符串 s ,返回其 最长 的 字母序连续子字符串 的长度。
示例 1:
输入:s = "abacaba"
输出:2
解释:共有 4 个不同的字母序连续子字符串 "a"、"b"、"c" 和 "ab" 。
"ab" 是最长的字母序连续子字符串。
示例 2:
输入:s = "abcde"
输出:5
解释:"abcde" 是最长的字母序连续子字符串。
提示:
1 <= s.length <= 105s由小写英文字母组成
Metadata
- Link: Length of the Longest Alphabetical Continuous Substring
- Difficulty: Medium
- Tag:
An alphabetical continuous string is a string consisting of consecutive letters in the alphabet. In other words, it is any substring of the string "abcdefghijklmnopqrstuvwxyz".
- For example,
"abc"is an alphabetical continuous string, while"acb"and"za"are not.
Given a string s consisting of lowercase letters only, return the length of the longest alphabetical continuous substring.
Example 1:
Input: s = "abacaba"
Output: 2
Explanation: There are 4 distinct continuous substrings: "a", "b", "c" and "ab".
"ab" is the longest continuous substring.
Example 2:
Input: s = "abcde"
Output: 5
Explanation: "abcde" is the longest continuous substring.
Constraints:
1 <= s.length <= 105sconsists of only English lowercase letters.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int longestContinuousSubstring(string s) {
int n = int(s.size());
int res = 1;
int cur = 1;
for (int i = 1; i < n; i++) {
if (s[i] == s[i - 1] + 1) {
++cur;
res = max(res, cur);
} else {
cur = 1;
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 反转二叉树的奇数层
- Difficulty: Medium
- Tag:
给你一棵 完美 二叉树的根节点 root ,请你反转这棵树中每个 奇数 层的节点值。
- 例如,假设第 3 层的节点值是
[2,1,3,4,7,11,29,18],那么反转后它应该变成[18,29,11,7,4,3,1,2]。
反转后,返回树的根节点。
完美 二叉树需满足:二叉树的所有父节点都有两个子节点,且所有叶子节点都在同一层。
节点的 层数 等于该节点到根节点之间的边数。
示例 1:
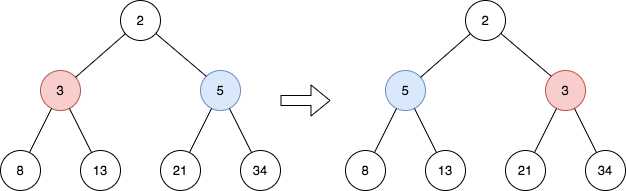
输入:root = [2,3,5,8,13,21,34]
输出:[2,5,3,8,13,21,34]
解释:
这棵树只有一个奇数层。
在第 1 层的节点分别是 3、5 ,反转后为 5、3 。
示例 2:

输入:root = [7,13,11]
输出:[7,11,13]
解释:
在第 1 层的节点分别是 13、11 ,反转后为 11、13 。
示例 3:
输入:root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
输出:[0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
解释:奇数层由非零值组成。
在第 1 层的节点分别是 1、2 ,反转后为 2、1 。
在第 3 层的节点分别是 1、1、1、1、2、2、2、2 ,反转后为 2、2、2、2、1、1、1、1 。
提示:
- 树中的节点数目在范围
[1, 214]内 0 <= Node.val <= 105root是一棵 完美 二叉树
Metadata
- Link: Reverse Odd Levels of Binary Tree
- Difficulty: Medium
- Tag:
Given the root of a perfect binary tree, reverse the node values at each odd level of the tree.
- For example, suppose the node values at level 3 are
[2,1,3,4,7,11,29,18], then it should become[18,29,11,7,4,3,1,2].
Return the root of the reversed tree.
A binary tree is perfect if all parent nodes have two children and all leaves are on the same level.
The level of a node is the number of edges along the path between it and the root node.
Example 1:

Input: root = [2,3,5,8,13,21,34]
Output: [2,5,3,8,13,21,34]
Explanation:
The tree has only one odd level.
The nodes at level 1 are 3, 5 respectively, which are reversed and become 5, 3.
Example 2:

Input: root = [7,13,11]
Output: [7,11,13]
Explanation:
The nodes at level 1 are 13, 11, which are reversed and become 11, 13.
Example 3:
Input: root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
Output: [0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
Explanation:
The odd levels have non-zero values.
The nodes at level 1 were 1, 2, and are 2, 1 after the reversal.
The nodes at level 3 were 1, 1, 1, 1, 2, 2, 2, 2, and are 2, 2, 2, 2, 1, 1, 1, 1 after the reversal.
Constraints:
- The number of nodes in the tree is in the range
[1, 214]. 0 <= Node.val <= 105rootis a perfect binary tree.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
#ifdef LOCAL
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
#endif
struct node {
TreeNode *t{nullptr};
int dep{0};
};
class Solution {
public:
TreeNode *reverseOddLevels(TreeNode *root) {
queue<node> q;
q.push(node{
.t = root,
.dep = 0,
});
auto vec = vector<vector<node>>(20, vector<node>{});
while (!q.empty()) {
auto front = q.front();
q.pop();
vec[front.dep].push_back(front);
if (front.t->left) {
q.push(node{
.t = front.t->left,
.dep = front.dep + 1,
});
}
if (front.t->right) {
q.push(node{
.t = front.t->right,
.dep = front.dep + 1,
});
}
}
for (int i = 1; i < 20; i += 2) {
int n = int(vec[i].size());
for (int j = 0, k = n - 1; j < k; j++, k--) {
swap(vec[i][j].t->val, vec[i][k].t->val);
}
}
return root;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 字符串的前缀分数和
- Difficulty: Hard
- Tag:
给你一个长度为 n 的数组 words ,该数组由 非空 字符串组成。
定义字符串 word 的 分数 等于以 word 作为 前缀 的 words[i] 的数目。
- 例如,如果
words = ["a", "ab", "abc", "cab"],那么"ab"的分数是2,因为"ab"是"ab"和"abc"的一个前缀。
返回一个长度为 n 的数组 answer ,其中 answer[i] 是 words[i] 的每个非空前缀的分数 总和 。
注意:字符串视作它自身的一个前缀。
示例 1:
输入:words = ["abc","ab","bc","b"]
输出:[5,4,3,2]
解释:对应每个字符串的答案如下:
- "abc" 有 3 个前缀:"a"、"ab" 和 "abc" 。
- 2 个字符串的前缀为 "a" ,2 个字符串的前缀为 "ab" ,1 个字符串的前缀为 "abc" 。
总计 answer[0] = 2 + 2 + 1 = 5 。
- "ab" 有 2 个前缀:"a" 和 "ab" 。
- 2 个字符串的前缀为 "a" ,2 个字符串的前缀为 "ab" 。
总计 answer[1] = 2 + 2 = 4 。
- "bc" 有 2 个前缀:"b" 和 "bc" 。
- 2 个字符串的前缀为 "b" ,1 个字符串的前缀为 "bc" 。
总计 answer[2] = 2 + 1 = 3 。
- "b" 有 1 个前缀:"b"。
- 2 个字符串的前缀为 "b" 。
总计 answer[3] = 2 。
示例 2:
输入:words = ["abcd"]
输出:[4]
解释:
"abcd" 有 4 个前缀 "a"、"ab"、"abc" 和 "abcd"。
每个前缀的分数都是 1 ,总计 answer[0] = 1 + 1 + 1 + 1 = 4 。
提示:
1 <= words.length <= 10001 <= words[i].length <= 1000words[i]由小写英文字母组成
Metadata
- Link: Sum of Prefix Scores of Strings
- Difficulty: Hard
- Tag:
You are given an array words of size n consisting of non-empty strings.
We define the score of a string word as the number of strings words[i] such that word is a prefix of words[i].
- For example, if
words = ["a", "ab", "abc", "cab"], then the score of"ab"is2, since"ab"is a prefix of both"ab"and"abc".
Return an array answer of size n where answer[i] is the sum of scores of every non-empty prefix of words[i].
Note that a string is considered as a prefix of itself.
Example 1:
Input: words = ["abc","ab","bc","b"]
Output: [5,4,3,2]
Explanation: The answer for each string is the following:
- "abc" has 3 prefixes: "a", "ab", and "abc".
- There are 2 strings with the prefix "a", 2 strings with the prefix "ab", and 1 string with the prefix "abc".
The total is answer[0] = 2 + 2 + 1 = 5.
- "ab" has 2 prefixes: "a" and "ab".
- There are 2 strings with the prefix "a", and 2 strings with the prefix "ab".
The total is answer[1] = 2 + 2 = 4.
- "bc" has 2 prefixes: "b" and "bc".
- There are 2 strings with the prefix "b", and 1 string with the prefix "bc".
The total is answer[2] = 2 + 1 = 3.
- "b" has 1 prefix: "b".
- There are 2 strings with the prefix "b".
The total is answer[3] = 2.
Example 2:
Input: words = ["abcd"]
Output: [4]
Explanation:
"abcd" has 4 prefixes: "a", "ab", "abc", and "abcd".
Each prefix has a score of one, so the total is answer[0] = 1 + 1 + 1 + 1 = 4.
Constraints:
1 <= words.length <= 10001 <= words[i].length <= 1000words[i]consists of lowercase English letters.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
constexpr int N = 1e6 + 10;
struct TRIE {
struct node {
int son[26];
int cnt;
node() {
memset(son, -1, sizeof son);
cnt = 0;
}
} t[N];
int rt, cnt;
void init() {
rt = 0;
t[0] = node();
cnt = 0;
}
void insert(const std::string &s) {
int cur_rt = rt;
for (const auto &c : s) {
if (t[cur_rt].son[c - 'a'] == -1) {
++cnt;
t[cnt] = node();
t[cur_rt].son[c - 'a'] = cnt;
}
cur_rt = t[cur_rt].son[c - 'a'];
++t[cur_rt].cnt;
}
}
int query(const std::string &s) {
int res = 0;
int cur_rt = rt;
for (const auto &c : s) {
cur_rt = t[cur_rt].son[c - 'a'];
res += t[cur_rt].cnt;
}
return res;
}
} tr;
class Solution {
public:
vector<int> sumPrefixScores(vector<string> &words) {
tr.init();
for (const auto &w : words) {
tr.insert(w);
}
auto res = vector<int>();
for (const auto &w : words) {
res.push_back(tr.query(w));
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif