跳转至

52.n-queens-ii

Statement

Metadata

n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

 

示例 1：

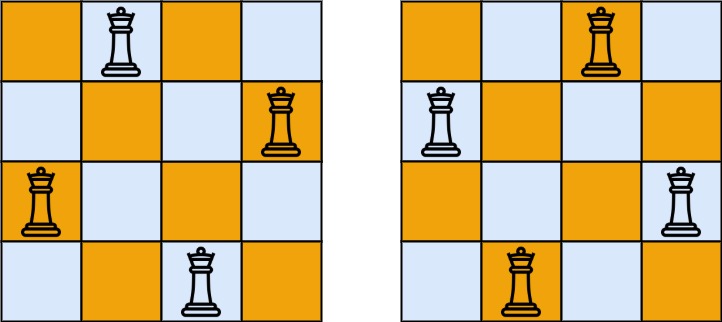
输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：1

 

提示：

  • 1 <= n <= 9

Metadata

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return the number of distinct solutions to the n-queens puzzle.

 

Example 1:

Input: n = 4
Output: 2
Explanation: There are two distinct solutions to the 4-queens puzzle as shown.

Example 2:

Input: n = 1
Output: 1

 

Constraints:

  • 1 <= n <= 9

Solution

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    static const int N = 1e2 + 10;

    int n, res;
    int g[N][N];

    bool ok(int x, int y) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (!(x == i && y == j)) {
                    if (g[i][j] == 1) {
                        if (i == x)
                            return false;
                        if (j == y)
                            return false;
                        if (i + j == x + y)
                            return false;
                        if (i - j == x - y)
                            return false;
                    }
                }
            }
        }
        return true;
    }

    void dfs(int cur) {
        if (cur == n + 1) {
            ++res;
            return;
        }
        for (int i = 1; i <= n; ++i) {
            if (ok(cur, i)) {
                g[cur][i] = 1;
                dfs(cur + 1);
                g[cur][i] = 0;
            }
        }
    }

    int totalNQueens(int n) {
        this->n = n;
        res = 0;
        memset(g, 0, sizeof g);

        dfs(1);

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif
最后更新: October 11, 2023
回到页面顶部