weekly-contest-274

A

Statement

简体中文English

Metadata

Link: 检查是否所有 A 都在 B 之前
Difficulty: Easy
Tag: 字符串

给你一个仅由字符 'a' 和 'b' 组成的字符串 s 。如果字符串中每个 'a' 都出现在每个 'b' 之前，返回 true ；否则，返回 false 。

示例 1：

输入：s = "aaabbb"
输出：true
解释：
'a' 位于下标 0、1 和 2 ；而 'b' 位于下标 3、4 和 5 。
因此，每个 'a' 都出现在每个 'b' 之前，所以返回 true 。

示例 2：

输入：s = "abab"
输出：false
解释：
存在一个 'a' 位于下标 2 ，而一个 'b' 位于下标 1 。
因此，不能满足每个 'a' 都出现在每个 'b' 之前，所以返回 false 。

示例 3：

输入：s = "bbb"
输出：true
解释：
不存在 'a' ，因此可以视作每个 'a' 都出现在每个 'b' 之前，所以返回 true 。

提示：

1 <= s.length <= 100
s[i] 为 'a' 或 'b'

Metadata

Link: Check if All A's Appears Before All B's
Difficulty: Easy
Tag: String

Given a string s consisting of only the characters 'a' and 'b', return true if every 'a' appears before every 'b' in the string. Otherwise, return false.

Example 1:

Input: s = "aaabbb"
Output: true
Explanation:
The 'a's are at indices 0, 1, and 2, while the 'b's are at indices 3, 4, and 5.
Hence, every 'a' appears before every 'b' and we return true.

Example 2:

Input: s = "abab"
Output: false
Explanation:
There is an 'a' at index 2 and a 'b' at index 1.
Hence, not every 'a' appears before every 'b' and we return false.

Example 3:

Input: s = "bbb"
Output: true
Explanation:
There are no 'a's, hence, every 'a' appears before every 'b' and we return true.

Constraints:

1 <= s.length <= 100
s[i] is either 'a' or 'b'.

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define lowbit(x) ((x) & (-(x)))
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    bool checkString(const string &s) {
        int f = 0;
        for (const auto &c : s) {
            if (c == 'a') {
                if (f)
                    return false;
            }

            if (c == 'b') {
                f = 1;
            }
        }

        return true;
    }
};

#ifdef LOCAL

int main() {
    auto s = Solution();

    assert_eq(s.checkString("aaabbb"), true);
    assert_eq(s.checkString("abab"), false);
    assert_eq(s.checkString("bbb"), true);

    return 0;
}

#endif

B

Statement

简体中文English

Metadata

Link: 银行中的激光束数量
Difficulty: Medium
Tag: 数组 数学 字符串 矩阵

银行内部的防盗安全装置已经激活。给你一个下标从 0 开始的二进制字符串数组 bank ，表示银行的平面图，这是一个大小为 m x n 的二维矩阵。 bank[i] 表示第 i 行的设备分布，由若干 '0' 和若干 '1' 组成。'0' 表示单元格是空的，而 '1' 表示单元格有一个安全设备。

对任意两个安全设备而言，如果同时满足下面两个条件，则二者之间存在一个激光束：

两个设备位于两个 不同行 ：r₁ 和 r₂ ，其中 r₁ < r₂ 。
满足 r₁ < i < r₂ 的所有行 i ，都 没有安全设备 。

激光束是独立的，也就是说，一个激光束既不会干扰另一个激光束，也不会与另一个激光束合并成一束。

返回银行中激光束的总数量。

示例 1：

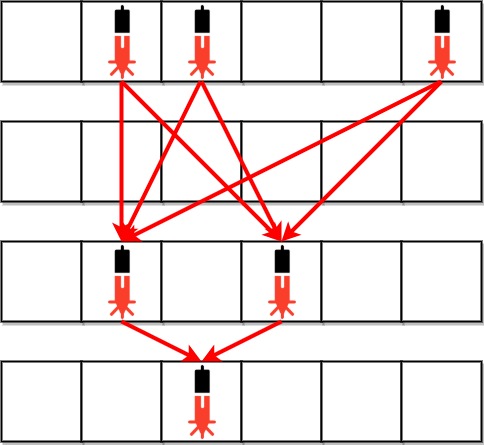
输入：bank = ["011001","000000","010100","001000"]
输出：8
解释：在下面每组设备对之间，存在一条激光束。总共是 8 条激光束：
 * bank[0][1] – bank[2][1]
 * bank[0][1] – bank[2][3]
 * bank[0][2] – bank[2][1]
 * bank[0][2] – bank[2][3]
 * bank[0][5] – bank[2][1]
 * bank[0][5] – bank[2][3]
 * bank[2][1] – bank[3][2]
 * bank[2][3] – bank[3][2]
注意，第 0 行和第 3 行上的设备之间不存在激光束。
这是因为第 2 行存在安全设备，这不满足第 2 个条件。

示例 2：

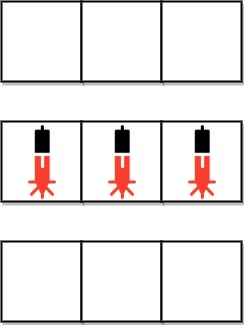
输入：bank = ["000","111","000"]
输出：0
解释：不存在两个位于不同行的设备

提示：

m == bank.length
n == bank[i].length
1 <= m, n <= 500
bank[i][j] 为 '0' 或 '1'

Metadata

Link: Number of Laser Beams in a Bank
Difficulty: Medium
Tag: Array Math String Matrix

Anti-theft security devices are activated inside a bank. You are given a 0-indexed binary string array bank representing the floor plan of the bank, which is an m x n 2D matrix. bank[i] represents the i^th row, consisting of '0's and '1's. '0' means the cell is empty, while'1' means the cell has a security device.

There is one laser beam between any two security devices if both conditions are met:

The two devices are located on two different rows: r₁ and r₂, where r₁ < r₂.
For each row i where r₁ < i < r₂, there are no security devices in the i^th row.

Laser beams are independent, i.e., one beam does not interfere nor join with another.

Return the total number of laser beams in the bank.

Example 1:

Input: bank = ["011001","000000","010100","001000"]
Output: 8
Explanation: Between each of the following device pairs, there is one beam. In total, there are 8 beams:
 * bank[0][1] – bank[2][1]
 * bank[0][1] – bank[2][3]
 * bank[0][2] – bank[2][1]
 * bank[0][2] – bank[2][3]
 * bank[0][5] – bank[2][1]
 * bank[0][5] – bank[2][3]
 * bank[2][1] – bank[3][2]
 * bank[2][3] – bank[3][2]
Note that there is no beam between any device on the 0^th row with any on the 3^rd row.
This is because the 2^nd row contains security devices, which breaks the second condition.

Example 2:

Input: bank = ["000","111","000"]
Output: 0
Explanation: There does not exist two devices located on two different rows.

Constraints:

m == bank.length
n == bank[i].length
1 <= m, n <= 500
bank[i][j] is either '0' or '1'.

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define lowbit(x) ((x) & (-(x)))
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    int numberOfBeams(const vector<string> &bank) {
        int n = bank.size();
        int m = bank[0].size();
        int res = 0;
        int pre = 0;
        int now = 0;
        for (int i = 0; i < n; i++) {
            now = 0;
            for (int j = 0; j < m; j++) {
                now += (bank[i][j] == '1');
            }
            res += now * pre;
            if (now) {
                pre = now;
            }
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    auto s = Solution();

    assert_eq(s.numberOfBeams(vector<string>{"011001", "000000", "010100", "001000"}), 8);
    return 0;
}

#endif

C

Statement

简体中文English

Metadata

Link: 摧毁小行星
Difficulty: Medium
Tag: 贪心 数组 排序

给你一个整数 mass ，它表示一颗行星的初始质量。再给你一个整数数组 asteroids ，其中 asteroids[i] 是第 i 颗小行星的质量。

你可以按 任意顺序 重新安排小行星的顺序，然后让行星跟它们发生碰撞。如果行星碰撞时的质量 大于等于 小行星的质量，那么小行星被摧毁，并且行星会获得这颗小行星的质量。否则，行星将被摧毁。

如果所有小行星都能被摧毁，请返回 true ，否则返回 false 。

示例 1：

输入：mass = 10, asteroids = [3,9,19,5,21]
输出：true
解释：一种安排小行星的方式为 [9,19,5,3,21] ：
- 行星与质量为 9 的小行星碰撞。新的行星质量为：10 + 9 = 19
- 行星与质量为 19 的小行星碰撞。新的行星质量为：19 + 19 = 38
- 行星与质量为 5 的小行星碰撞。新的行星质量为：38 + 5 = 43
- 行星与质量为 3 的小行星碰撞。新的行星质量为：43 + 3 = 46
- 行星与质量为 21 的小行星碰撞。新的行星质量为：46 + 21 = 67
所有小行星都被摧毁。

示例 2：

输入：mass = 5, asteroids = [4,9,23,4]
输出：false
解释：
行星无论如何没法获得足够质量去摧毁质量为 23 的小行星。
行星把别的小行星摧毁后，质量为 5 + 4 + 9 + 4 = 22 。
它比 23 小，所以无法摧毁最后一颗小行星。

提示：

1 <= mass <= 10⁵
1 <= asteroids.length <= 10⁵
1 <= asteroids[i] <= 10⁵

Metadata

Link: Destroying Asteroids
Difficulty: Medium
Tag: Greedy Array Sorting

You are given an integer mass, which represents the original mass of a planet. You are further given an integer array asteroids, where asteroids[i] is the mass of the i^th asteroid.

You can arrange for the planet to collide with the asteroids in any arbitrary order. If the mass of the planet is greater than or equal to the mass of the asteroid, the asteroid is destroyed and the planet gains the mass of the asteroid. Otherwise, the planet is destroyed.

Return true if all asteroids can be destroyed. Otherwise, return false.

Example 1:

Input: mass = 10, asteroids = [3,9,19,5,21]
Output: true
Explanation: One way to order the asteroids is [9,19,5,3,21]:
- The planet collides with the asteroid with a mass of 9. New planet mass: 10 + 9 = 19
- The planet collides with the asteroid with a mass of 19. New planet mass: 19 + 19 = 38
- The planet collides with the asteroid with a mass of 5. New planet mass: 38 + 5 = 43
- The planet collides with the asteroid with a mass of 3. New planet mass: 43 + 3 = 46
- The planet collides with the asteroid with a mass of 21. New planet mass: 46 + 21 = 67
All asteroids are destroyed.

Example 2:

Input: mass = 5, asteroids = [4,9,23,4]
Output: false
Explanation: 
The planet cannot ever gain enough mass to destroy the asteroid with a mass of 23.
After the planet destroys the other asteroids, it will have a mass of 5 + 4 + 9 + 4 = 22.
This is less than 23, so a collision would not destroy the last asteroid.

Constraints:

1 <= mass <= 10⁵
1 <= asteroids.length <= 10⁵
1 <= asteroids[i] <= 10⁵

D

Statement

简体中文English

Metadata

Link: 参加会议的最多员工数
Difficulty: Hard
Tag: 深度优先搜索 图 拓扑排序

一个公司准备组织一场会议，邀请名单上有 n 位员工。公司准备了一张圆形的桌子，可以坐下 任意数目 的员工。

员工编号为 0 到 n - 1 。每位员工都有一位喜欢的员工，每位员工 当且仅当 他被安排在喜欢员工的旁边，他才会参加会议。每位员工喜欢的员工不会是他自己。

给你一个下标从 0 开始的整数数组 favorite ，其中 favorite[i] 表示第 i 位员工喜欢的员工。请你返回参加会议的 最多员工数目 。

示例 1：

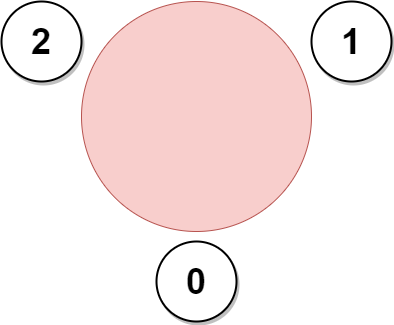
输入：favorite = [2,2,1,2]
输出：3
解释：
上图展示了公司邀请员工 0，1 和 2 参加会议以及他们在圆桌上的座位。
没办法邀请所有员工参与会议，因为员工 2 没办法同时坐在 0，1 和 3 员工的旁边。
注意，公司也可以邀请员工 1，2 和 3 参加会议。
所以最多参加会议的员工数目为 3 。

示例 2：

输入：favorite = [1,2,0]
输出：3
解释：
每个员工都至少是另一个员工喜欢的员工。所以公司邀请他们所有人参加会议的前提是所有人都参加了会议。
座位安排同图 1 所示：
- 员工 0 坐在员工 2 和 1 之间。
- 员工 1 坐在员工 0 和 2 之间。
- 员工 2 坐在员工 1 和 0 之间。
参与会议的最多员工数目为 3 。

示例 3：

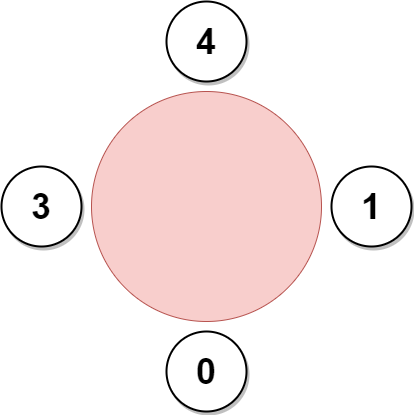
输入：favorite = [3,0,1,4,1]
输出：4
解释：
上图展示了公司可以邀请员工 0，1，3 和 4 参加会议以及他们在圆桌上的座位。
员工 2 无法参加，因为他喜欢的员工 0 旁边的座位已经被占领了。
所以公司只能不邀请员工 2 。
参加会议的最多员工数目为 4 。

提示：

n == favorite.length
2 <= n <= 10⁵
0 <= favorite[i] <= n - 1
favorite[i] != i

Metadata

Link: Maximum Employees to Be Invited to a Meeting
Difficulty: Hard
Tag: Depth-First Search Graph Topological Sort

A company is organizing a meeting and has a list of n employees, waiting to be invited. They have arranged for a large circular table, capable of seating any number of employees.

The employees are numbered from 0 to n - 1. Each employee has a favorite person and they will attend the meeting only if they can sit next to their favorite person at the table. The favorite person of an employee is not themself.

Given a 0-indexed integer array favorite, where favorite[i] denotes the favorite person of the i^th employee, return the maximum number of employees that can be invited to the meeting.

Example 1:

Input: favorite = [2,2,1,2]
Output: 3
Explanation:
The above figure shows how the company can invite employees 0, 1, and 2, and seat them at the round table.
All employees cannot be invited because employee 2 cannot sit beside employees 0, 1, and 3, simultaneously.
Note that the company can also invite employees 1, 2, and 3, and give them their desired seats.
The maximum number of employees that can be invited to the meeting is 3.

Example 2:

Input: favorite = [1,2,0]
Output: 3
Explanation: 
Each employee is the favorite person of at least one other employee, and the only way the company can invite them is if they invite every employee.
The seating arrangement will be the same as that in the figure given in example 1:
- Employee 0 will sit between employees 2 and 1.
- Employee 1 will sit between employees 0 and 2.
- Employee 2 will sit between employees 1 and 0.
The maximum number of employees that can be invited to the meeting is 3.

Example 3:

Input: favorite = [3,0,1,4,1]
Output: 4
Explanation:
The above figure shows how the company will invite employees 0, 1, 3, and 4, and seat them at the round table.
Employee 2 cannot be invited because the two spots next to their favorite employee 1 are taken.
So the company leaves them out of the meeting.
The maximum number of employees that can be invited to the meeting is 4.

Constraints:

n == favorite.length
2 <= n <= 10⁵
0 <= favorite[i] <= n - 1
favorite[i] != i

最后更新: October 11, 2023