weekly-contest-297
A
Statement
Metadata
- Link: 计算应缴税款总额
- Difficulty: Easy
- Tag:
数组
给你一个下标从 0 开始的二维整数数组 brackets ,其中 brackets[i] = [upperi, percenti] ,表示第 i 个税级的上限是 upperi ,征收的税率为 percenti 。税级按上限 从低到高排序(在满足 0 < i < brackets.length 的前提下,upperi-1 < upperi)。
税款计算方式如下:
- 不超过
upper0的收入按税率percent0缴纳 - 接着
upper1 - upper0的部分按税率percent1缴纳 - 然后
upper2 - upper1的部分按税率percent2缴纳 - 以此类推
给你一个整数 income 表示你的总收入。返回你需要缴纳的税款总额。与标准答案误差不超 10-5 的结果将被视作正确答案。
示例 1:
输入:brackets = [[3,50],[7,10],[12,25]], income = 10
输出:2.65000
解释:
前 $3 的税率为 50% 。需要支付税款 $3 * 50% = $1.50 。
接下来 $7 - $3 = $4 的税率为 10% 。需要支付税款 $4 * 10% = $0.40 。
最后 $10 - $7 = $3 的税率为 25% 。需要支付税款 $3 * 25% = $0.75 。
需要支付的税款总计 $1.50 + $0.40 + $0.75 = $2.65 。
示例 2:
输入:brackets = [[1,0],[4,25],[5,50]], income = 2
输出:0.25000
解释:
前 $1 的税率为 0% 。需要支付税款 $1 * 0% = $0 。
剩下 $1 的税率为 25% 。需要支付税款 $1 * 25% = $0.25 。
需要支付的税款总计 $0 + $0.25 = $0.25 。
示例 3:
输入:brackets = [[2,50]], income = 0
输出:0.00000
解释:
没有收入,无需纳税,需要支付的税款总计 $0 。
提示:
1 <= brackets.length <= 1001 <= upperi <= 10000 <= percenti <= 1000 <= income <= 1000upperi按递增顺序排列upperi中的所有值 互不相同- 最后一个税级的上限大于等于
income
Metadata
- Link: Calculate Amount Paid in Taxes
- Difficulty: Easy
- Tag:
Array
You are given a 0-indexed 2D integer array brackets where brackets[i] = [upperi, percenti] means that the ith tax bracket has an upper bound of upperi and is taxed at a rate of percenti. The brackets are sorted by upper bound (i.e. upperi-1 < upperi for 0 < i < brackets.length).
Tax is calculated as follows:
- The first
upper0dollars earned are taxed at a rate ofpercent0. - The next
upper1 - upper0dollars earned are taxed at a rate ofpercent1. - The next
upper2 - upper1dollars earned are taxed at a rate ofpercent2. - And so on.
You are given an integer income representing the amount of money you earned. Return the amount of money that you have to pay in taxes. Answers within 10-5 of the actual answer will be accepted.
Example 1:
Input: brackets = [[3,50],[7,10],[12,25]], income = 10
Output: 2.65000
Explanation:
The first 3 dollars you earn are taxed at 50%. You have to pay $3 * 50% = $1.50 dollars in taxes.
The next 7 - 3 = 4 dollars you earn are taxed at 10%. You have to pay $4 * 10% = $0.40 dollars in taxes.
The final 10 - 7 = 3 dollars you earn are taxed at 25%. You have to pay $3 * 25% = $0.75 dollars in taxes.
You have to pay a total of $1.50 + $0.40 + $0.75 = $2.65 dollars in taxes.
Example 2:
Input: brackets = [[1,0],[4,25],[5,50]], income = 2
Output: 0.25000
Explanation:
The first dollar you earn is taxed at 0%. You have to pay $1 * 0% = $0 dollars in taxes.
The second dollar you earn is taxed at 25%. You have to pay $1 * 25% = $0.25 dollars in taxes.
You have to pay a total of $0 + $0.25 = $0.25 dollars in taxes.
Example 3:
Input: brackets = [[2,50]], income = 0
Output: 0.00000
Explanation:
You have no income to tax, so you have to pay a total of $0 dollars in taxes.
Constraints:
1 <= brackets.length <= 1001 <= upperi <= 10000 <= percenti <= 1000 <= income <= 1000upperiis sorted in ascending order.- All the values of
upperiare unique. - The upper bound of the last tax bracket is greater than or equal to
income.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
double calculateTax(vector<vector<int>> &brackets, int income) {
double res = 0;
int pre = 0;
int n = int(brackets.size());
for (int i = 0; i < n; i++) {
if (income <= brackets[i][0]) {
res += 1.0 * (income - pre) * brackets[i][1] / 100.0;
break;
}
res += 1.0 * (brackets[i][0] - pre) * brackets[i][1] / 100.0;
pre = brackets[i][0];
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 网格中的最小路径代价
- Difficulty: Medium
- Tag:
动态规划
给你一个下标从 0 开始的整数矩阵 grid ,矩阵大小为 m x n ,由从 0 到 m * n - 1 的不同整数组成。你可以在此矩阵中,从一个单元格移动到 下一行 的任何其他单元格。如果你位于单元格 (x, y) ,且满足 x < m - 1 ,你可以移动到 (x + 1, 0), (x + 1, 1), …, (x + 1, n - 1) 中的任何一个单元格。注意: 在最后一行中的单元格不能触发移动。
每次可能的移动都需要付出对应的代价,代价用一个下标从 0 开始的二维数组 moveCost 表示,该数组大小为 (m * n) x n ,其中 moveCost[i][j] 是从值为 i 的单元格移动到下一行第 j 列单元格的代价。从 grid 最后一行的单元格移动的代价可以忽略。
grid 一条路径的代价是:所有路径经过的单元格的 值之和 加上 所有移动的 代价之和 。从 第一行 任意单元格出发,返回到达 最后一行 任意单元格的最小路径代价。
示例 1:
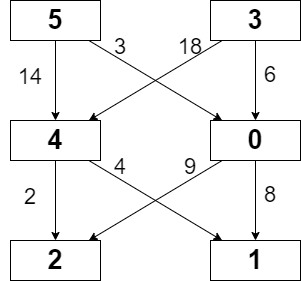
输入:grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
输出:17
解释:最小代价的路径是 5 -> 0 -> 1 。
- 路径途经单元格值之和 5 + 0 + 1 = 6 。
- 从 5 移动到 0 的代价为 3 。
- 从 0 移动到 1 的代价为 8 。
路径总代价为 6 + 3 + 8 = 17 。
示例 2:
输入:grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
输出:6
解释:
最小代价的路径是 2 -> 3 。
- 路径途经单元格值之和 2 + 3 = 5 。
- 从 2 移动到 3 的代价为 1 。
路径总代价为 5 + 1 = 6 。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 50grid由从0到m * n - 1的不同整数组成moveCost.length == m * nmoveCost[i].length == n1 <= moveCost[i][j] <= 100
Metadata
- Link: Minimum Path Cost in a Grid
- Difficulty: Medium
- Tag:
Dynamic Programming
You are given a 0-indexed m x n integer matrix grid consisting of distinct integers from 0 to m * n - 1. You can move in this matrix from a cell to any other cell in the next row. That is, if you are in cell (x, y) such that x < m - 1, you can move to any of the cells (x + 1, 0), (x + 1, 1), …, (x + 1, n - 1). Note that it is not possible to move from cells in the last row.
Each possible move has a cost given by a 0-indexed 2D array moveCost of size (m * n) x n, where moveCost[i][j] is the cost of moving from a cell with value i to a cell in column j of the next row. The cost of moving from cells in the last row of grid can be ignored.
The cost of a path in grid is the sum of all values of cells visited plus the sum of costs of all the moves made. Return the minimum cost of a path that starts from any cell in the first row and ends at any cell in the last row.
Example 1:

Input: grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
Output: 17
Explanation: The path with the minimum possible cost is the path 5 -> 0 -> 1.
- The sum of the values of cells visited is 5 + 0 + 1 = 6.
- The cost of moving from 5 to 0 is 3.
- The cost of moving from 0 to 1 is 8.
So the total cost of the path is 6 + 3 + 8 = 17.
Example 2:
Input: grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
Output: 6
Explanation: The path with the minimum possible cost is the path 2 -> 3.
- The sum of the values of cells visited is 2 + 3 = 5.
- The cost of moving from 2 to 3 is 1.
So the total cost of this path is 5 + 1 = 6.
Constraints:
m == grid.lengthn == grid[i].length2 <= m, n <= 50gridconsists of distinct integers from0tom * n - 1.moveCost.length == m * nmoveCost[i].length == n1 <= moveCost[i][j] <= 100
Solution
#include <bits/stdc++.h>
#include <algorithm>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int minPathCost(vector<vector<int>> &grid, vector<vector<int>> &moveCost) {
int m = grid.size();
int n = grid[0].size();
vector<vector<int>> dp(m, vector<int>(n, 0x3f3f3f3f));
for (int i = 0; i < n; i++) {
dp[0][i] = grid[0][i];
}
for (int i = 1; i < m; ++i) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
dp[i][j] = min(dp[i][j], dp[i - 1][k] + moveCost[grid[i - 1][k]][j] + grid[i][j]);
}
}
}
return *min_element(dp[m - 1].begin(), dp[m - 1].end());
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 公平分发饼干
- Difficulty: Medium
- Tag:
回溯
给你一个整数数组 cookies ,其中 cookies[i] 表示在第 i 个零食包中的饼干数量。另给你一个整数 k 表示等待分发零食包的孩子数量,所有 零食包都需要分发。在同一个零食包中的所有饼干都必须分发给同一个孩子,不能分开。
分发的 不公平程度 定义为单个孩子在分发过程中能够获得饼干的最大总数。
返回所有分发的最小不公平程度。
示例 1:
输入:cookies = [8,15,10,20,8], k = 2
输出:31
解释:一种最优方案是 [8,15,8] 和 [10,20] 。
- 第 1 个孩子分到 [8,15,8] ,总计 8 + 15 + 8 = 31 块饼干。
- 第 2 个孩子分到 [10,20] ,总计 10 + 20 = 30 块饼干。
分发的不公平程度为 max(31,30) = 31 。
可以证明不存在不公平程度小于 31 的分发方案。
示例 2:
输入:cookies = [6,1,3,2,2,4,1,2], k = 3
输出:7
解释:一种最优方案是 [6,1]、[3,2,2] 和 [4,1,2] 。
- 第 1 个孩子分到 [6,1] ,总计 6 + 1 = 7 块饼干。
- 第 2 个孩子分到 [3,2,2] ,总计 3 + 2 + 2 = 7 块饼干。
- 第 3 个孩子分到 [4,1,2] ,总计 4 + 1 + 2 = 7 块饼干。
分发的不公平程度为 max(7,7,7) = 7 。
可以证明不存在不公平程度小于 7 的分发方案。
提示:
2 <= cookies.length <= 81 <= cookies[i] <= 1052 <= k <= cookies.length
Metadata
- Link: Fair Distribution of Cookies
- Difficulty: Medium
- Tag:
Backtracking
You are given an integer array cookies, where cookies[i] denotes the number of cookies in the ith bag. You are also given an integer k that denotes the number of children to distribute all the bags of cookies to. All the cookies in the same bag must go to the same child and cannot be split up.
The unfairness of a distribution is defined as the maximum total cookies obtained by a single child in the distribution.
Return the minimum unfairness of all distributions.
Example 1:
Input: cookies = [8,15,10,20,8], k = 2
Output: 31
Explanation: One optimal distribution is [8,15,8] and [10,20]
- The 1st child receives [8,15,8] which has a total of 8 + 15 + 8 = 31 cookies.
- The 2nd child receives [10,20] which has a total of 10 + 20 = 30 cookies.
The unfairness of the distribution is max(31,30) = 31.
It can be shown that there is no distribution with an unfairness less than 31.
Example 2:
Input: cookies = [6,1,3,2,2,4,1,2], k = 3
Output: 7
Explanation: One optimal distribution is [6,1], [3,2,2], and [4,1,2]
- The 1st child receives [6,1] which has a total of 6 + 1 = 7 cookies.
- The 2nd child receives [3,2,2] which has a total of 3 + 2 + 2 = 7 cookies.
- The 3rd child receives [4,1,2] which has a total of 4 + 1 + 2 = 7 cookies.
The unfairness of the distribution is max(7,7,7) = 7.
It can be shown that there is no distribution with an unfairness less than 7.
Constraints:
2 <= cookies.length <= 81 <= cookies[i] <= 1052 <= k <= cookies.length
Solution
#include <bits/stdc++.h>
#include <algorithm>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int ans;
int k;
void dfs(vector<int> &cookies, vector<int> &children, int cur_ans) {
if (cur_ans >= ans) {
return;
}
if (cookies.empty()) {
ans = cur_ans;
return;
}
auto c = cookies.back();
cookies.pop_back();
for (int i = 0; i < k; i++) {
children[i] += c;
dfs(cookies, children, max(cur_ans, children[i]));
children[i] -= c;
}
cookies.push_back(c);
}
int distributeCookies(vector<int> &cookies, int k) {
ans = 0x3f3f3f3f;
this->k = k;
auto children = vector<int>(k, 0);
dfs(cookies, children, 0);
return ans;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 公司命名
- Difficulty: Hard
- Tag:
给你一个字符串数组 ideas 表示在公司命名过程中使用的名字列表。公司命名流程如下:
- 从
ideas中选择 2 个 不同 名字,称为ideaA和ideaB。 - 交换
ideaA和ideaB的首字母。 - 如果得到的两个新名字 都 不在
ideas中,那么ideaA ideaB(串联ideaA和ideaB,中间用一个空格分隔)是一个有效的公司名字。 - 否则,不是一个有效的名字。
返回 不同 且有效的公司名字的数目。
示例 1:
输入:ideas = ["coffee","donuts","time","toffee"]
输出:6
解释:下面列出一些有效的选择方案:
- ("coffee", "donuts"):对应的公司名字是 "doffee conuts" 。
- ("donuts", "coffee"):对应的公司名字是 "conuts doffee" 。
- ("donuts", "time"):对应的公司名字是 "tonuts dime" 。
- ("donuts", "toffee"):对应的公司名字是 "tonuts doffee" 。
- ("time", "donuts"):对应的公司名字是 "dime tonuts" 。
- ("toffee", "donuts"):对应的公司名字是 "doffee tonuts" 。
因此,总共有 6 个不同的公司名字。
下面列出一些无效的选择方案:
- ("coffee", "time"):在原数组中存在交换后形成的名字 "toffee" 。
- ("time", "toffee"):在原数组中存在交换后形成的两个名字。
- ("coffee", "toffee"):在原数组中存在交换后形成的两个名字。
示例 2:
输入:ideas = ["lack","back"]
输出:0
解释:不存在有效的选择方案。因此,返回 0 。
提示:
2 <= ideas.length <= 5 * 1041 <= ideas[i].length <= 10ideas[i]由小写英文字母组成ideas中的所有字符串 互不相同
Metadata
- Link: Naming a Company
- Difficulty: Hard
- Tag:
You are given an array of strings ideas that represents a list of names to be used in the process of naming a company. The process of naming a company is as follows:
- Choose 2 distinct names from
ideas, call themideaAandideaB. - Swap the first letters of
ideaAandideaBwith each other. - If both of the new names are not found in the original
ideas, then the nameideaA ideaB(the concatenation ofideaAandideaB, separated by a space) is a valid company name. - Otherwise, it is not a valid name.
Return the number of distinct valid names for the company.
Example 1:
Input: ideas = ["coffee","donuts","time","toffee"]
Output: 6
Explanation: The following selections are valid:
- ("coffee", "donuts"): The company name created is "doffee conuts".
- ("donuts", "coffee"): The company name created is "conuts doffee".
- ("donuts", "time"): The company name created is "tonuts dime".
- ("donuts", "toffee"): The company name created is "tonuts doffee".
- ("time", "donuts"): The company name created is "dime tonuts".
- ("toffee", "donuts"): The company name created is "doffee tonuts".
Therefore, there are a total of 6 distinct company names.
The following are some examples of invalid selections:
- ("coffee", "time"): The name "toffee" formed after swapping already exists in the original array.
- ("time", "toffee"): Both names are still the same after swapping and exist in the original array.
- ("coffee", "toffee"): Both names formed after swapping already exist in the original array.
Example 2:
Input: ideas = ["lack","back"]
Output: 0
Explanation: There are no valid selections. Therefore, 0 is returned.
Constraints:
2 <= ideas.length <= 5 * 1041 <= ideas[i].length <= 10ideas[i]consists of lowercase English letters.- All the strings in
ideasare unique.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int idx;
map<string, int> id_map;
int getId(const std::string &s) {
if (id_map.count(s) == 0) {
id_map[s] = ++idx;
}
return id_map[s];
}
long long distinctNames(vector<string> &ideas) {
idx = 0;
id_map = {};
int n = int(ideas.size());
ll res = 1ll * n * n;
vector<int> id(n);
vector<int> first_char(n);
for (int i = 0; i < n; i++) {
id[i] = getId(ideas[i].substr(1));
first_char[i] = ideas[i][0] - 'a';
}
map<int, bitset<26>> mp;
vector<int> cnt(26, 0);
vector<vector<int>> fcnt(26, vector<int>(26, 0));
for (int i = 0; i < n; i++) {
mp[id[i]].set(first_char[i]);
++cnt[first_char[i]];
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < 26; j++) {
if (mp[id[i]].test(j)) {
++fcnt[j][first_char[i]];
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < 26; j++) {
if (mp[id[i]].test(j)) {
res -= cnt[j];
} else {
res -= fcnt[first_char[i]][j];
}
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif