weekly-contest-317
A
Statement
Metadata
- Link: 可被三整除的偶数的平均值
- Difficulty: Easy
- Tag:
给你一个由正整数组成的整数数组 nums ,返回其中可被 3 整除的所有偶数的平均值。
注意:n 个元素的平均值等于 n 个元素 求和 再除以 n ,结果 向下取整 到最接近的整数。
示例 1:
输入:nums = [1,3,6,10,12,15]
输出:9
解释:6 和 12 是可以被 3 整除的偶数。(6 + 12) / 2 = 9 。
示例 2:
输入:nums = [1,2,4,7,10]
输出:0
解释:不存在满足题目要求的整数,所以返回 0 。
提示:
1 <= nums.length <= 10001 <= nums[i] <= 1000
Metadata
- Link: Average Value of Even Numbers That Are Divisible by Three
- Difficulty: Easy
- Tag:
Given an integer array nums of positive integers, return the average value of all even integers that are divisible by 3.
Note that the average of n elements is the sum of the n elements divided by n and rounded down to the nearest integer.
Example 1:
Input: nums = [1,3,6,10,12,15]
Output: 9
Explanation: 6 and 12 are even numbers that are divisible by 3. (6 + 12) / 2 = 9.
Example 2:
Input: nums = [1,2,4,7,10]
Output: 0
Explanation: There is no single number that satisfies the requirement, so return 0.
Constraints:
1 <= nums.length <= 10001 <= nums[i] <= 1000
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int averageValue(vector<int> &nums) {
int sum = 0;
int num = 0;
for (const auto &a : nums) {
if (a % 3 == 0 && a % 2 == 0) {
sum += a;
num++;
}
}
if (num == 0) {
return 0;
}
return sum / num;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 最流行的视频创作者
- Difficulty: Medium
- Tag:
给你两个字符串数组 creators 和 ids ,和一个整数数组 views ,所有数组的长度都是 n 。平台上第 i 个视频者是 creator[i] ,视频分配的 id 是 ids[i] ,且播放量为 views[i] 。
视频创作者的 流行度 是该创作者的 所有 视频的播放量的 总和 。请找出流行度 最高 创作者以及该创作者播放量 最大 的视频的 id 。
- 如果存在多个创作者流行度都最高,则需要找出所有符合条件的创作者。
- 如果某个创作者存在多个播放量最高的视频,则只需要找出字典序最小的
id。
返回一个二维字符串数组 answer ,其中 answer[i] = [creatori, idi] 表示 creatori 的流行度 最高 且其最流行的视频 id 是 idi ,可以按任何顺序返回该结果。
示例 1:
输入:creators = ["alice","bob","alice","chris"], ids = ["one","two","three","four"], views = [5,10,5,4]
输出:[["alice","one"],["bob","two"]]
解释:
alice 的流行度是 5 + 5 = 10 。
bob 的流行度是 10 。
chris 的流行度是 4 。
alice 和 bob 是流行度最高的创作者。
bob 播放量最高的视频 id 为 "two" 。
alice 播放量最高的视频 id 是 "one" 和 "three" 。由于 "one" 的字典序比 "three" 更小,所以结果中返回的 id 是 "one" 。
示例 2:
输入:creators = ["alice","alice","alice"], ids = ["a","b","c"], views = [1,2,2]
输出:[["alice","b"]]
解释:
id 为 "b" 和 "c" 的视频都满足播放量最高的条件。
由于 "b" 的字典序比 "c" 更小,所以结果中返回的 id 是 "b" 。
提示:
n == creators.length == ids.length == views.length1 <= n <= 1051 <= creators[i].length, ids[i].length <= 5creators[i]和ids[i]仅由小写英文字母组成0 <= views[i] <= 105
Metadata
- Link: Most Popular Video Creator
- Difficulty: Medium
- Tag:
You are given two string arrays creators and ids, and an integer array views, all of length n. The ith video on a platform was created by creator[i], has an id of ids[i], and has views[i] views.
The popularity of a creator is the sum of the number of views on all of the creator's videos. Find the creator with the highest popularity and the id of their most viewed video.
- If multiple creators have the highest popularity, find all of them.
- If multiple videos have the highest view count for a creator, find the lexicographically smallest id.
Return a 2D array of strings answer where answer[i] = [creatori, idi] means that creatori has the highest popularity and idi is the id of their most popular video. The answer can be returned in any order.
Example 1:
Input: creators = ["alice","bob","alice","chris"], ids = ["one","two","three","four"], views = [5,10,5,4]
Output: [["alice","one"],["bob","two"]]
Explanation:
The popularity of alice is 5 + 5 = 10.
The popularity of bob is 10.
The popularity of chris is 4.
alice and bob are the most popular creators.
For bob, the video with the highest view count is "two".
For alice, the videos with the highest view count are "one" and "three". Since "one" is lexicographically smaller than "three", it is included in the answer.
Example 2:
Input: creators = ["alice","alice","alice"], ids = ["a","b","c"], views = [1,2,2]
Output: [["alice","b"]]
Explanation:
The videos with id "b" and "c" have the highest view count.
Since "b" is lexicographically smaller than "c", it is included in the answer.
Constraints:
n == creators.length == ids.length == views.length1 <= n <= 1051 <= creators[i].length, ids[i].length <= 5creators[i]andids[i]consist only of lowercase English letters.0 <= views[i] <= 105
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
struct node {
ll sum = 0;
int max_view = -1;
string id = "";
};
class Solution {
public:
vector<vector<string>> mostPopularCreator(vector<string> &creators, vector<string> &ids, vector<int> &views) {
int n = int(creators.size());
auto mp = map<string, node>();
ll mx_views = 0;
for (int i = 0; i < n; i++) {
const auto &c = creators[i];
const auto &id = ids[i];
int view = views[i];
mp[c].sum += view;
if (view > mp[c].max_view || (view == mp[c].max_view && id < mp[c].id)) {
mp[c].max_view = view;
mp[c].id = id;
}
mx_views = max(mx_views, mp[c].sum);
}
auto res = vector<vector<string>>();
for (const auto &[k, v] : mp) {
if (v.sum == mx_views) {
res.push_back(vector<string>({k, v.id}));
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 美丽整数的最小增量
- Difficulty: Medium
- Tag:
给你两个正整数 n 和 target 。
如果某个整数每一位上的数字相加小于或等于 target ,则认为这个整数是一个 美丽整数 。
找出并返回满足 n + x 是 美丽整数 的最小非负整数 x 。生成的输入保证总可以使 n 变成一个美丽整数。
示例 1:
输入:n = 16, target = 6
输出:4
解释:最初,n 是 16 ,且其每一位数字的和是 1 + 6 = 7 。在加 4 之后,n 变为 20 且每一位数字的和变成 2 + 0 = 2 。可以证明无法加上一个小于 4 的非负整数使 n 变成一个美丽整数。
示例 2:
输入:n = 467, target = 6
输出:33
解释:最初,n 是 467 ,且其每一位数字的和是 4 + 6 + 7 = 17 。在加 33 之后,n 变为 500 且每一位数字的和变成 5 + 0 + 0 = 5 。可以证明无法加上一个小于 33 的非负整数使 n 变成一个美丽整数。示例 3:
输入:n = 1, target = 1
输出:0
解释:最初,n 是 1 ,且其每一位数字的和是 1 ,已经小于等于 target 。
提示:
1 <= n <= 10121 <= target <= 150- 生成的输入保证总可以使
n变成一个美丽整数。
Metadata
- Link: Minimum Addition to Make Integer Beautiful
- Difficulty: Medium
- Tag:
You are given two positive integers n and target.
An integer is considered beautiful if the sum of its digits is less than or equal to target.
Return the minimum non-negative integer x such that n + x is beautiful. The input will be generated such that it is always possible to make n beautiful.
Example 1:
Input: n = 16, target = 6
Output: 4
Explanation: Initially n is 16 and its digit sum is 1 + 6 = 7. After adding 4, n becomes 20 and digit sum becomes 2 + 0 = 2. It can be shown that we can not make n beautiful with adding non-negative integer less than 4.
Example 2:
Input: n = 467, target = 6
Output: 33
Explanation: Initially n is 467 and its digit sum is 4 + 6 + 7 = 17. After adding 33, n becomes 500 and digit sum becomes 5 + 0 + 0 = 5. It can be shown that we can not make n beautiful with adding non-negative integer less than 33.
Example 3:
Input: n = 1, target = 1
Output: 0
Explanation: Initially n is 1 and its digit sum is 1, which is already smaller than or equal to target.
Constraints:
1 <= n <= 10121 <= target <= 150- The input will be generated such that it is always possible to make
nbeautiful.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int getTarget(ll n) {
int res = 0;
while (n) {
res += n % 10;
n /= 10;
}
return res;
}
long long makeIntegerBeautiful(long long n, int target) {
auto vec = vector<int>();
ll _n = n;
while (_n) {
vec.push_back(_n % 10);
_n /= 10;
}
vec.push_back(0);
int sze = int(vec.size());
// for (int i = 0; i < sze; i++) {
// cout << i << " " << vec[i] << endl;
// }
for (int i = 0; i < sze - 1; i++) {
int sum = accumulate(all(vec), 0);
if (sum <= target) {
break;
}
vec[i] = 0;
++vec[i + 1];
for (int j = i + 1; j < sze - 1; j++) {
if (vec[j] < 10) {
break;
}
vec[j] = 0;
++vec[j + 1];
}
}
// while (!vec.empty() && vec.back() == 0) {
// vec.pop_back();
// }
reverse(all(vec));
ll m = 0;
for (const auto &a : vec) {
m = m * 10 + a;
}
return m - n;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 移除子树后的二叉树高度
- Difficulty: Hard
- Tag:
给你一棵 二叉树 的根节点 root ,树中有 n 个节点。每个节点都可以被分配一个从 1 到 n 且互不相同的值。另给你一个长度为 m 的数组 queries 。
你必须在树上执行 m 个 独立 的查询,其中第 i 个查询你需要执行以下操作:
- 从树中 移除 以
queries[i]的值作为根节点的子树。题目所用测试用例保证queries[i]不 等于根节点的值。
返回一个长度为 m 的数组 answer ,其中 answer[i] 是执行第 i 个查询后树的高度。
注意:
- 查询之间是独立的,所以在每个查询执行后,树会回到其 初始 状态。
- 树的高度是从根到树中某个节点的 最长简单路径中的边数 。
示例 1:
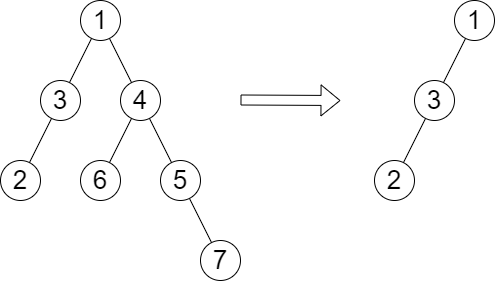
输入:root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
输出:[2]
解释:上图展示了从树中移除以 4 为根节点的子树。
树的高度是 2(路径为 1 -> 3 -> 2)。
示例 2:
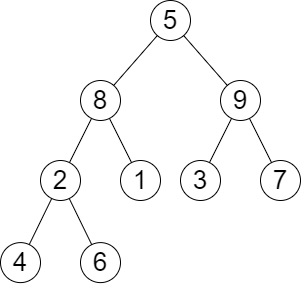
输入:root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
输出:[3,2,3,2]
解释:执行下述查询:
- 移除以 3 为根节点的子树。树的高度变为 3(路径为 5 -> 8 -> 2 -> 4)。
- 移除以 2 为根节点的子树。树的高度变为 2(路径为 5 -> 8 -> 1)。
- 移除以 4 为根节点的子树。树的高度变为 3(路径为 5 -> 8 -> 2 -> 6)。
- 移除以 8 为根节点的子树。树的高度变为 2(路径为 5 -> 9 -> 3)。
提示:
- 树中节点的数目是
n 2 <= n <= 1051 <= Node.val <= n- 树中的所有值 互不相同
m == queries.length1 <= m <= min(n, 104)1 <= queries[i] <= nqueries[i] != root.val
Metadata
- Link: Height of Binary Tree After Subtree Removal Queries
- Difficulty: Hard
- Tag:
You are given the root of a binary tree with n nodes. Each node is assigned a unique value from 1 to n. You are also given an array queries of size m.
You have to perform m independent queries on the tree where in the ith query you do the following:
- Remove the subtree rooted at the node with the value
queries[i]from the tree. It is guaranteed thatqueries[i]will not be equal to the value of the root.
Return an array answer of size m where answer[i] is the height of the tree after performing the ith query.
Note:
- The queries are independent, so the tree returns to its initial state after each query.
- The height of a tree is the number of edges in the longest simple path from the root to some node in the tree.
Example 1:

Input: root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
Output: [2]
Explanation: The diagram above shows the tree after removing the subtree rooted at node with value 4.
The height of the tree is 2 (The path 1 -> 3 -> 2).
Example 2:

Input: root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
Output: [3,2,3,2]
Explanation: We have the following queries:
- Removing the subtree rooted at node with value 3. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 4).
- Removing the subtree rooted at node with value 2. The height of the tree becomes 2 (The path 5 -> 8 -> 1).
- Removing the subtree rooted at node with value 4. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 6).
- Removing the subtree rooted at node with value 8. The height of the tree becomes 2 (The path 5 -> 9 -> 3).
Constraints:
- The number of nodes in the tree is
n. 2 <= n <= 1051 <= Node.val <= n- All the values in the tree are unique.
m == queries.length1 <= m <= min(n, 104)1 <= queries[i] <= nqueries[i] != root.val
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
#ifdef LOCAL
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
#endif
struct node {
int left_h = 0;
int right_h = 0;
int deep = 0;
};
class Solution {
public:
map<int, int> res;
map<int, node> tree_info;
int n;
int max_height;
int preDFS(TreeNode *root, int deep) {
++n;
int val = root->val;
auto &ti = tree_info[val];
ti.deep = deep;
max_height = max(max_height, deep);
if (root->left) {
ti.left_h = preDFS(root->left, deep + 1) + 1;
}
if (root->right) {
ti.right_h = preDFS(root->right, deep + 1) + 1;
}
return max(ti.left_h, ti.right_h);
}
void dfs(TreeNode *root, int mmax_height) {
int val = root->val;
const auto &ti = tree_info[val];
if (ti.left_h == ti.right_h) {
return;
}
if (ti.left_h > ti.right_h) {
int height = max(ti.deep + ti.right_h, mmax_height);
res[root->left->val] = height;
dfs(root->left, height);
} else {
int height = max(ti.deep + ti.left_h, mmax_height);
res[root->right->val] = height;
dfs(root->right, height);
}
}
vector<int> treeQueries(TreeNode *root, vector<int> &queries) {
res.clear();
tree_info.clear();
n = 0;
max_height = 0;
preDFS(root, 0);
dfs(root, -1);
// cout << max_hight << endl;
auto ans = vector<int>();
for (const auto &q : queries) {
if (res.count(q)) {
ans.push_back(res[q]);
} else {
ans.push_back(max_height);
}
}
return ans;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif