weekly-contest-320

A

Statement

简体中文English

Metadata

Link: 数组中不等三元组的数目
Difficulty: Easy
Tag:

给你一个下标从 0 开始的正整数数组 nums 。请你找出并统计满足下述条件的三元组 (i, j, k) 的数目：

0 <= i < j < k < nums.length
nums[i]、nums[j] 和 nums[k] 两两不同 。
- 换句话说：nums[i] != nums[j]、nums[i] != nums[k] 且 nums[j] != nums[k] 。

返回满足上述条件三元组的数目。

示例 1：

输入：nums = [4,4,2,4,3]
输出：3
解释：下面列出的三元组均满足题目条件：
- (0, 2, 4) 因为 4 != 2 != 3
- (1, 2, 4) 因为 4 != 2 != 3
- (2, 3, 4) 因为 2 != 4 != 3
共计 3 个三元组，返回 3 。
注意 (2, 0, 4) 不是有效的三元组，因为 2 > 0 。

示例 2：

输入：nums = [1,1,1,1,1]
输出：0
解释：不存在满足条件的三元组，所以返回 0 。

提示：

3 <= nums.length <= 100
1 <= nums[i] <= 1000

Metadata

Link: Number of Unequal Triplets in Array
Difficulty: Easy
Tag:

You are given a 0-indexed array of positive integers nums. Find the number of triplets (i, j, k) that meet the following conditions:

0 <= i < j < k < nums.length
nums[i], nums[j], and nums[k] are pairwise distinct.
- In other words, nums[i] != nums[j], nums[i] != nums[k], and nums[j] != nums[k].

Return the number of triplets that meet the conditions.

Example 1:

Input: nums = [4,4,2,4,3]
Output: 3
Explanation: The following triplets meet the conditions:
- (0, 2, 4) because 4 != 2 != 3
- (1, 2, 4) because 4 != 2 != 3
- (2, 3, 4) because 2 != 4 != 3
Since there are 3 triplets, we return 3.
Note that (2, 0, 4) is not a valid triplet because 2 > 0.

Example 2:

Input: nums = [1,1,1,1,1]
Output: 0
Explanation: No triplets meet the conditions so we return 0.

Constraints:

3 <= nums.length <= 100
1 <= nums[i] <= 1000

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    int unequalTriplets(vector<int> &nums) {
        int n = int(nums.size());

        int res = 0;

        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                for (int k = j + 1; k < n; k++) {
                    int a = nums[i];
                    int b = nums[j];
                    int c = nums[k];

                    if (a != b && b != c && a != c) {
                        ++res;
                    }
                }
            }
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

简体中文English

Metadata

Link: 二叉搜索树最近节点查询
Difficulty: Medium
Tag:

给你一个 二叉搜索树 的根节点 root ，和一个由正整数组成、长度为 n 的数组 queries 。

请你找出一个长度为 n 的二维答案数组 answer ，其中 answer[i] = [min_i, max_i] ：

min_i 是树中小于等于 queries[i] 的 最大值 。如果不存在这样的值，则使用 -1 代替。
max_i 是树中大于等于 queries[i] 的 最小值 。如果不存在这样的值，则使用 -1 代替。

返回数组 answer 。

示例 1 ：

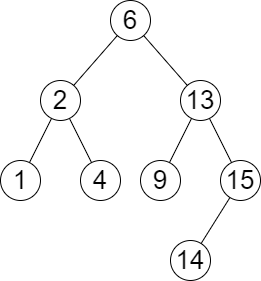
输入：root = [6,2,13,1,4,9,15,null,null,null,null,null,null,14], queries = [2,5,16]
输出：[[2,2],[4,6],[15,-1]]
解释：按下面的描述找出并返回查询的答案：
- 树中小于等于 2 的最大值是 2 ，且大于等于 2 的最小值也是 2 。所以第一个查询的答案是 [2,2] 。
- 树中小于等于 5 的最大值是 4 ，且大于等于 5 的最小值是 6 。所以第二个查询的答案是 [4,6] 。
- 树中小于等于 16 的最大值是 15 ，且大于等于 16 的最小值不存在。所以第三个查询的答案是 [15,-1] 。

示例 2 ：

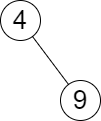
输入：root = [4,null,9], queries = [3]
输出：[[-1,4]]
解释：树中不存在小于等于 3 的最大值，且大于等于 3 的最小值是 4 。所以查询的答案是 [-1,4] 。

提示：

树中节点的数目在范围 [2, 10⁵] 内
1 <= Node.val <= 10⁶
n == queries.length
1 <= n <= 10⁵
1 <= queries[i] <= 10⁶

Metadata

Link: Closest Nodes Queries in a Binary Search Tree
Difficulty: Medium
Tag:

You are given the root of a binary search tree and an array queries of size n consisting of positive integers.

Find a 2D array answer of size n where answer[i] = [min_i, max_i]:

min_i is the largest value in the tree that is smaller than or equal to queries[i]. If a such value does not exist, add -1 instead.
max_i is the smallest value in the tree that is greater than or equal to queries[i]. If a such value does not exist, add -1 instead.

Return the array answer.

Example 1:

Input: root = [6,2,13,1,4,9,15,null,null,null,null,null,null,14], queries = [2,5,16]
Output: [[2,2],[4,6],[15,-1]]
Explanation: We answer the queries in the following way:
- The largest number that is smaller or equal than 2 in the tree is 2, and the smallest number that is greater or equal than 2 is still 2. So the answer for the first query is [2,2].
- The largest number that is smaller or equal than 5 in the tree is 4, and the smallest number that is greater or equal than 5 is 6. So the answer for the second query is [4,6].
- The largest number that is smaller or equal than 16 in the tree is 15, and the smallest number that is greater or equal than 16 does not exist. So the answer for the third query is [15,-1].

Example 2:

Input: root = [4,null,9], queries = [3]
Output: [[-1,4]]
Explanation: The largest number that is smaller or equal to 3 in the tree does not exist, and the smallest number that is greater or equal to 3 is 4. So the answer for the query is [-1,4].

Constraints:

The number of nodes in the tree is in the range [2, 10⁵].
1 <= Node.val <= 10⁶
n == queries.length
1 <= n <= 10⁵
1 <= queries[i] <= 10⁶

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

#ifdef LOCAL

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

#endif

class Solution {
public:
    vector<int> a;
    void dfs(TreeNode *rt) {
        if (!rt) {
            return;
        }

        a.push_back(rt->val);
        dfs(rt->left);
        dfs(rt->right);
    }

    vector<vector<int>> closestNodes(TreeNode *root, vector<int> &queries) {
        a.clear();
        dfs(root);

        sort(all(a));

        auto res = vector<vector<int>>();

        for (const auto &q : queries) {
            auto pos = lower_bound(all(a), q);
            int mi = -1;
            int mx = -1;

            if (pos == a.end()) {
                --pos;
                mi = *pos;
            } else {
                mx = *pos;
                if (mx == q) {
                    mi = mx;
                } else if (pos != a.begin()) {
                    --pos;
                    mi = *pos;
                }
            }

            res.push_back({mi, mx});
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

简体中文English

Metadata

Link: 到达首都的最少油耗
Difficulty: Medium
Tag:

给你一棵 n 个节点的树（一个无向、连通、无环图），每个节点表示一个城市，编号从 0 到 n - 1 ，且恰好有 n - 1 条路。0 是首都。给你一个二维整数数组 roads ，其中 roads[i] = [a_i, b_i] ，表示城市 a_i 和 b_i 之间有一条 双向路 。

每个城市里有一个代表，他们都要去首都参加一个会议。

每座城市里有一辆车。给你一个整数 seats 表示每辆车里面座位的数目。

城市里的代表可以选择乘坐所在城市的车，或者乘坐其他城市的车。相邻城市之间一辆车的油耗是一升汽油。

请你返回到达首都最少需要多少升汽油。

示例 1：

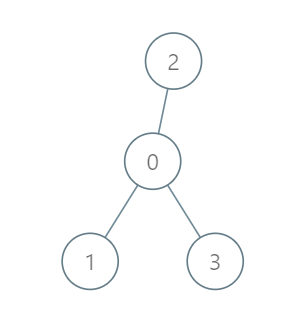
输入：roads = [[0,1],[0,2],[0,3]], seats = 5
输出：3
解释：
- 代表 1 直接到达首都，消耗 1 升汽油。
- 代表 2 直接到达首都，消耗 1 升汽油。
- 代表 3 直接到达首都，消耗 1 升汽油。
最少消耗 3 升汽油。

示例 2：

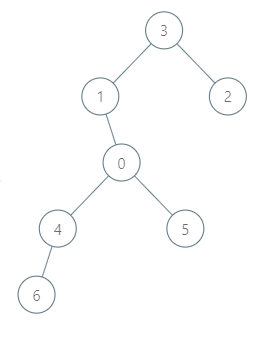
输入：roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
输出：7
解释：
- 代表 2 到达城市 3 ，消耗 1 升汽油。
- 代表 2 和代表 3 一起到达城市 1 ，消耗 1 升汽油。
- 代表 2 和代表 3 一起到达首都，消耗 1 升汽油。
- 代表 1 直接到达首都，消耗 1 升汽油。
- 代表 5 直接到达首都，消耗 1 升汽油。
- 代表 6 到达城市 4 ，消耗 1 升汽油。
- 代表 4 和代表 6 一起到达首都，消耗 1 升汽油。
最少消耗 7 升汽油。

示例 3：

输入：roads = [], seats = 1
输出：0
解释：没有代表需要从别的城市到达首都。

提示：

1 <= n <= 10⁵
roads.length == n - 1
roads[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
roads 表示一棵合法的树。
1 <= seats <= 10⁵

Metadata

Link: Minimum Fuel Cost to Report to the Capital
Difficulty: Medium
Tag:

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of n cities numbered from 0 to n - 1 and exactly n - 1 roads. The capital city is city 0. You are given a 2D integer array roads where roads[i] = [a_i, b_i] denotes that there exists a bidirectional road connecting cities a_i and b_i.

There is a meeting for the representatives of each city. The meeting is in the capital city.

There is a car in each city. You are given an integer seats that indicates the number of seats in each car.

A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel.

Return the minimum number of liters of fuel to reach the capital city.

Example 1:

Input: roads = [[0,1],[0,2],[0,3]], seats = 5
Output: 3
Explanation: 
- Representative₁ goes directly to the capital with 1 liter of fuel.
- Representative₂ goes directly to the capital with 1 liter of fuel.
- Representative₃ goes directly to the capital with 1 liter of fuel.
It costs 3 liters of fuel at minimum. 
It can be proven that 3 is the minimum number of liters of fuel needed.

Example 2:

Input: roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
Output: 7
Explanation: 
- Representative₂ goes directly to city 3 with 1 liter of fuel.
- Representative₂ and representative₃ go together to city 1 with 1 liter of fuel.
- Representative₂ and representative₃ go together to the capital with 1 liter of fuel.
- Representative₁ goes directly to the capital with 1 liter of fuel.
- Representative₅ goes directly to the capital with 1 liter of fuel.
- Representative₆ goes directly to city 4 with 1 liter of fuel.
- Representative₄ and representative₆ go together to the capital with 1 liter of fuel.
It costs 7 liters of fuel at minimum. 
It can be proven that 7 is the minimum number of liters of fuel needed.

Example 3:

Input: roads = [], seats = 1
Output: 0
Explanation: No representatives need to travel to the capital city.

Constraints:

1 <= n <= 10⁵
roads.length == n - 1
roads[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
roads represents a valid tree.
1 <= seats <= 10⁵

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    vector<vector<int>> G;
    int seats;
    pair<ll, int> dfs(int u, int fa) {
        ll cost = 0;
        int cnt = 1;

        for (const auto &v : G[u]) {
            if (v == fa) {
                continue;
            }

            auto p = dfs(v, u);
            cost += p.first;
            cost += (p.second + seats - 1) / seats;
            cnt += p.second;
        }

        return make_pair(cost, cnt);
    }

    long long minimumFuelCost(vector<vector<int>> &roads, int seats) {
        int n = int(roads.size()) + 1;
        G = vector<vector<int>>(n + 1, vector<int>());
        this->seats = seats;

        for (const auto &r : roads) {
            int u = r[0];
            int v = r[1];
            G[u].push_back(v);
            G[v].push_back(u);
        }

        return dfs(0, -1).first;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

D

Statement

简体中文English

Metadata

Link: 完美分割的方案数
Difficulty: Hard
Tag:

给你一个字符串 s ，每个字符是数字 '1' 到 '9' ，再给你两个整数 k 和 minLength 。

如果对 s 的分割满足以下条件，那么我们认为它是一个完美分割：

s 被分成 k 段互不相交的子字符串。
每个子字符串长度都至少为 minLength 。
每个子字符串的第一个字符都是一个质数数字，最后一个字符都是一个 非质数 数字。质数数字为 '2' ，'3' ，'5' 和 '7' ，剩下的都是非质数数字。

请你返回 s 的完美分割数目。由于答案可能很大，请返回答案对 10⁹ + 7 取余后的结果。

一个 子字符串 是字符串中一段连续字符串序列。

示例 1：

输入：s = "23542185131", k = 3, minLength = 2
输出：3
解释：存在 3 种完美分割方案：
"2354 | 218 | 5131"
"2354 | 21851 | 31"
"2354218 | 51 | 31"

示例 2：

输入：s = "23542185131", k = 3, minLength = 3
输出：1
解释：存在一种完美分割方案："2354 | 218 | 5131" 。

示例 3：

输入：s = "3312958", k = 3, minLength = 1
输出：1
解释：存在一种完美分割方案："331 | 29 | 58" 。

提示：

1 <= k, minLength <= s.length <= 1000
s 每个字符都为数字 '1' 到 '9' 之一。

Metadata

Link: Number of Beautiful Partitions
Difficulty: Hard
Tag:

You are given a string s that consists of the digits '1' to '9' and two integers k and minLength.

A partition of s is called beautiful if:

s is partitioned into k non-intersecting substrings.
Each substring has a length of at least minLength.
Each substring starts with a prime digit and ends with a non-prime digit. Prime digits are '2', '3', '5', and '7', and the rest of the digits are non-prime.

Return the number of beautiful partitions of s. Since the answer may be very large, return it modulo 10⁹ + 7.

A substring is a contiguous sequence of characters within a string.

Example 1:

Input: s = "23542185131", k = 3, minLength = 2
Output: 3
Explanation: There exists three ways to create a beautiful partition:
"2354 | 218 | 5131"
"2354 | 21851 | 31"
"2354218 | 51 | 31"

Example 2:

Input: s = "23542185131", k = 3, minLength = 3
Output: 1
Explanation: There exists one way to create a beautiful partition: "2354 | 218 | 5131".

Example 3:

Input: s = "3312958", k = 3, minLength = 1
Output: 1
Explanation: There exists one way to create a beautiful partition: "331 | 29 | 58".

Constraints:

1 <= k, minLength <= s.length <= 1000
s consists of the digits '1' to '9'.

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    inline static constexpr int mod = 1e9 + 7;

    inline static constexpr bool is_prime[] = {
            0,
            0,
            1,
            1,
            0,
            1,
            0,
            1,
            0,
            0,
    };

    int beautifulPartitions(string s, int k, int minLength) {
        int n = int(s.size());

        auto f = vector<vector<int>>(n + 5, vector<int>(k + 5, 0));
        auto g = vector<vector<int>>(n + 5, vector<int>(k + 5, 0));

        f[0][0] = 1;

        for (int i = 1; i <= n; i++) {
            char c = s[i - 1];

            for (int o = 0; o <= k; o++) {
                g[i][o] = g[i - 1][o];
            }

            if (!is_prime[c - '0']) {
                int j = i - minLength + 1;

                if (j >= 1) {
                    for (int o = 1; o <= k; o++) {
                        f[i][o] = (f[i][o] + g[j][o - 1]) % mod;
                    }
                }
            }

            for (int o = 0; o <= k; o++) {
                if (is_prime[c - '0']) {
                    g[i][o] = (g[i][o] + f[i - 1][o]) % mod;
                }
            }
        }

        return f[n][k];
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

最后更新: October 11, 2023