跳转至

124.binary-tree-maximum-path-sum

Statement

Metadata

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

 

示例 1：

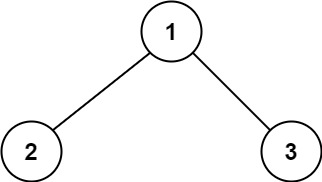
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

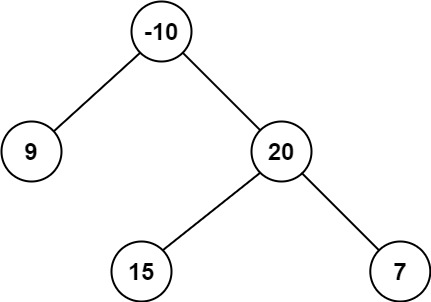
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

 

提示：

  • 树中节点数目范围是 [1, 3 * 104]
  • -1000 <= Node.val <= 1000

Metadata

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

 

Example 1:

Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

 

Constraints:

  • The number of nodes in the tree is in the range [1, 3 * 104].
  • -1000 <= Node.val <= 1000

Solution

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
from typing import Optional


class Solution:
    res = -1000

    def dfs(self, root: TreeNode) -> int:
        if not root:
            return 0

        left = self.dfs(root.left)
        right = self.dfs(root.right)
        val = root.val

        self.res = max(self.res, left + right + val,
                       left + val, right + val, val)
        return max(val, left + val, right + val)

    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        self.dfs(root)
        return self.res
最后更新: October 11, 2023
回到页面顶部