biweekly-contest-70

A

Statement

简体中文English

Metadata

• Link: 打折购买糖果的最小开销
• Difficulty: Easy
• Tag: 贪心 数组 排序

一家商店正在打折销售糖果。每购买 两个 糖果，商店会 免费 送一个糖果。

免费送的糖果唯一的限制是：它的价格需要小于等于购买的两个糖果价格的 较小值 。

• 比方说，总共有 4 个糖果，价格分别为 1 ，2 ，3 和 4 ，一位顾客买了价格为 2 和 3 的糖果，那么他可以免费获得价格为 1 的糖果，但不能获得价格为 4 的糖果。

给你一个下标从 0 开始的整数数组 cost ，其中 cost[i] 表示第 i 个糖果的价格，请你返回获得 所有 糖果的 最小 总开销。

 

示例 1：

输入：cost = [1,2,3]
输出：5
解释：我们购买价格为 2 和 3 的糖果，然后免费获得价格为 1 的糖果。
总开销为 2 + 3 = 5 。这是开销最小的 唯一 方案。
注意，我们不能购买价格为 1 和 3 的糖果，并免费获得价格为 2 的糖果。
这是因为免费糖果的价格必须小于等于购买的 2 个糖果价格的较小值。

示例 2：

输入：cost = [6,5,7,9,2,2]
输出：23
解释：最小总开销购买糖果方案为：
- 购买价格为 9 和 7 的糖果
- 免费获得价格为 6 的糖果
- 购买价格为 5 和 2 的糖果
- 免费获得价格为 2 的最后一个糖果
因此，最小总开销为 9 + 7 + 5 + 2 = 23 。

示例 3：

输入：cost = [5,5]
输出：10
解释：由于只有 2 个糖果，我们需要将它们都购买，而且没有免费糖果。
所以总最小开销为 5 + 5 = 10 。

 

提示：

• 1 <= cost.length <= 100
• 1 <= cost[i] <= 100

Metadata

• Link: Minimum Cost of Buying Candies With Discount
• Difficulty: Easy
• Tag: Greedy Array Sorting

A shop is selling candies at a discount. For every two candies sold, the shop gives a third candy for free.

The customer can choose any candy to take away for free as long as the cost of the chosen candy is less than or equal to the minimum cost of the two candies bought.

• For example, if there are 4 candies with costs 1, 2, 3, and 4, and the customer buys candies with costs 2 and 3, they can take the candy with cost 1 for free, but not the candy with cost 4.

Given a 0-indexed integer array cost, where cost[i] denotes the cost of the ith candy, return the minimum cost of buying all the candies.

 

Example 1:

Input: cost = [1,2,3]
Output: 5
Explanation: We buy the candies with costs 2 and 3, and take the candy with cost 1 for free.
The total cost of buying all candies is 2 + 3 = 5. This is the only way we can buy the candies.
Note that we cannot buy candies with costs 1 and 3, and then take the candy with cost 2 for free.
The cost of the free candy has to be less than or equal to the minimum cost of the purchased candies.

Example 2:

Input: cost = [6,5,7,9,2,2]
Output: 23
Explanation: The way in which we can get the minimum cost is described below:
- Buy candies with costs 9 and 7
- Take the candy with cost 6 for free
- We buy candies with costs 5 and 2
- Take the last remaining candy with cost 2 for free
Hence, the minimum cost to buy all candies is 9 + 7 + 5 + 2 = 23.

Example 3:

Input: cost = [5,5]
Output: 10
Explanation: Since there are only 2 candies, we buy both of them. There is not a third candy we can take for free.
Hence, the minimum cost to buy all candies is 5 + 5 = 10.

 

Constraints:

• 1 <= cost.length <= 100
• 1 <= cost[i] <= 100

Solution

C++

#include <bits/stdc++.h>

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif

using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define Mkp make_pair
#define All(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
// head

class Solution {
public:
    int minimumCost(vector<int>& cost) {
        sort(All(cost));
        int res = 0;
        while (cost.size() >= 3) {
            res += cost.back();
            cost.pop_back();
            res += cost.back();
            cost.pop_back();
            cost.pop_back();
        }

        for (auto& c : cost) {
            res += c;
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

简体中文English

Metadata

• Link: 统计隐藏数组数目
• Difficulty: Medium
• Tag: 数组 前缀和

给你一个下标从 0 开始且长度为 n 的整数数组 differences ，它表示一个长度为 n + 1 的 隐藏 数组 相邻 元素之间的 差值 。更正式的表述为：我们将隐藏数组记作 hidden ，那么 differences[i] = hidden[i + 1] - hidden[i] 。

同时给你两个整数 lower 和 upper ，它们表示隐藏数组中所有数字的值都在 闭 区间 [lower, upper] 之间。

• 比方说，differences = [1, -3, 4] ，lower = 1 ，upper = 6 ，那么隐藏数组是一个长度为 4 且所有值都在 1 和 6 （包含两者）之间的数组。
  • [3, 4, 1, 5] 和 [4, 5, 2, 6] 都是符合要求的隐藏数组。
  • [5, 6, 3, 7] 不符合要求，因为它包含大于 6 的元素。
  • [1, 2, 3, 4] 不符合要求，因为相邻元素的差值不符合给定数据。

请你返回 符合 要求的隐藏数组的数目。如果没有符合要求的隐藏数组，请返回 0 。

 

示例 1：

输入：differences = [1,-3,4], lower = 1, upper = 6
输出：2
解释：符合要求的隐藏数组为：
- [3, 4, 1, 5]
- [4, 5, 2, 6]
所以返回 2 。

示例 2：

输入：differences = [3,-4,5,1,-2], lower = -4, upper = 5
输出：4
解释：符合要求的隐藏数组为：
- [-3, 0, -4, 1, 2, 0]
- [-2, 1, -3, 2, 3, 1]
- [-1, 2, -2, 3, 4, 2]
- [0, 3, -1, 4, 5, 3]
所以返回 4 。

示例 3：

输入：differences = [4,-7,2], lower = 3, upper = 6
输出：0
解释：没有符合要求的隐藏数组，所以返回 0 。

 

提示：

• n == differences.length
• 1 <= n <= 105
• -105 <= differences[i] <= 105
• -105 <= lower <= upper <= 105

Metadata

• Link: Count the Hidden Sequences
• Difficulty: Medium
• Tag: Array Prefix Sum

You are given a 0-indexed array of n integers differences, which describes the differences between each pair of consecutive integers of a hidden sequence of length (n + 1). More formally, call the hidden sequence hidden, then we have that differences[i] = hidden[i + 1] - hidden[i].

You are further given two integers lower and upper that describe the inclusive range of values [lower, upper] that the hidden sequence can contain.

• For example, given differences = [1, -3, 4], lower = 1, upper = 6, the hidden sequence is a sequence of length 4 whose elements are in between 1 and 6 (inclusive).
  • [3, 4, 1, 5] and [4, 5, 2, 6] are possible hidden sequences.
  • [5, 6, 3, 7] is not possible since it contains an element greater than 6.
  • [1, 2, 3, 4] is not possible since the differences are not correct.

Return the number of possible hidden sequences there are. If there are no possible sequences, return 0.

 

Example 1:

Input: differences = [1,-3,4], lower = 1, upper = 6
Output: 2
Explanation: The possible hidden sequences are:
- [3, 4, 1, 5]
- [4, 5, 2, 6]
Thus, we return 2.

Example 2:

Input: differences = [3,-4,5,1,-2], lower = -4, upper = 5
Output: 4
Explanation: The possible hidden sequences are:
- [-3, 0, -4, 1, 2, 0]
- [-2, 1, -3, 2, 3, 1]
- [-1, 2, -2, 3, 4, 2]
- [0, 3, -1, 4, 5, 3]
Thus, we return 4.

Example 3:

Input: differences = [4,-7,2], lower = 3, upper = 6
Output: 0
Explanation: There are no possible hidden sequences. Thus, we return 0.

 

Constraints:

• n == differences.length
• 1 <= n <= 105
• -105 <= differences[i] <= 105
• -105 <= lower <= upper <= 105

Solution

C++

#include <bits/stdc++.h>

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif

using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define Mkp make_pair
#define All(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
// head

const ll INF = 0x3f3f3f3f3f3f3f3f;

class Solution {
public:
    int numberOfArrays(vector<int>& differences, int lower, int upper) {
        ll Max = -INF;
        ll Min = INF;
        ll ret = 0;

        for (auto& a : differences) {
            ret += a;
            Max = max(Max, ret);
            Min = min(Min, ret);
        }

        ll _lower = lower;
        ll _upper = upper;

        if (Min < 0) {
            _lower -= Min;
        }

        if (Max > 0) {
            _upper -= Max;
        }

        return max(0ll, _upper - _lower + 1);
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

简体中文English

Metadata

• Link: 价格范围内最高排名的 K 样物品
• Difficulty: Medium
• Tag: 广度优先搜索 数组 矩阵 排序 堆（优先队列）

给你一个下标从 0 开始的二维整数数组 grid ，它的大小为 m x n ，表示一个商店中物品的分布图。数组中的整数含义为：

• 0 表示无法穿越的一堵墙。
• 1 表示可以自由通过的一个空格子。
• 所有其他正整数表示该格子内的一样物品的价格。你可以自由经过这些格子。

从一个格子走到上下左右相邻格子花费 1 步。

同时给你一个整数数组 pricing 和 start ，其中 pricing = [low, high] 且 start = [row, col] ，表示你开始位置为 (row, col) ，同时你只对物品价格在 闭区间 [low, high] 之内的物品感兴趣。同时给你一个整数 k 。

你想知道给定范围 内 且 排名最高 的 k 件物品的 位置 。排名按照优先级从高到低的以下规则制定：

1. 距离：定义为从 start 到一件物品的最短路径需要的步数（较近 距离的排名更高）。
2. 价格：较低 价格的物品有更高优先级，但只考虑在给定范围之内的价格。
3. 行坐标：较小 行坐标的有更高优先级。
4. 列坐标：较小 列坐标的有更高优先级。

请你返回给定价格内排名最高的 k 件物品的坐标，将它们按照排名排序后返回。如果给定价格内少于 k 件物品，那么请将它们的坐标 全部 返回。

 

示例 1：

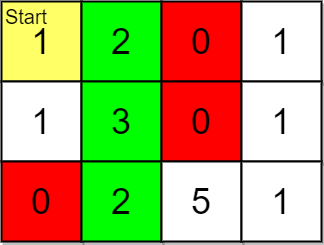
输入：grid = [[1,2,0,1],[1,3,0,1],[0,2,5,1]], pricing = [2,5], start = [0,0], k = 3
输出：[[0,1],[1,1],[2,1]]
解释：起点为 (0,0) 。
价格范围为 [2,5] ，我们可以选择的物品坐标为 (0,1)，(1,1)，(2,1) 和 (2,2) 。
这些物品的排名为：
- (0,1) 距离为 1
- (1,1) 距离为 2
- (2,1) 距离为 3
- (2,2) 距离为 4
所以，给定价格范围内排名最高的 3 件物品的坐标为 (0,1)，(1,1) 和 (2,1) 。

示例 2：

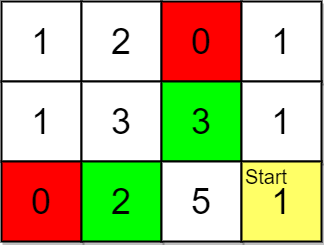
输入：grid = [[1,2,0,1],[1,3,3,1],[0,2,5,1]], pricing = [2,3], start = [2,3], k = 2
输出：[[2,1],[1,2]]
解释：起点为 (2,3) 。
价格范围为 [2,3] ，我们可以选择的物品坐标为 (0,1)，(1,1)，(1,2) 和 (2,1) 。
这些物品的排名为： 
- (2,1) 距离为 2 ，价格为 2
- (1,2) 距离为 2 ，价格为 3
- (1,1) 距离为 3
- (0,1) 距离为 4
所以，给定价格范围内排名最高的 2 件物品的坐标为 (2,1) 和 (1,2) 。

示例 3：

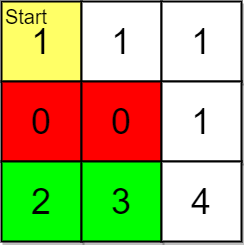
输入：grid = [[1,1,1],[0,0,1],[2,3,4]], pricing = [2,3], start = [0,0], k = 3
输出：[[2,1],[2,0]]
解释：起点为 (0,0) 。
价格范围为 [2,3] ，我们可以选择的物品坐标为 (2,0) 和 (2,1) 。
这些物品的排名为：
- (2,1) 距离为 5
- (2,0) 距离为 6
所以，给定价格范围内排名最高的 2 件物品的坐标为 (2,1) 和 (2,0) 。
注意，k = 3 但给定价格范围内只有 2 件物品。

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 0 <= grid[i][j] <= 105
• pricing.length == 2
• 2 <= low <= high <= 105
• start.length == 2
• 0 <= row <= m - 1
• 0 <= col <= n - 1
• grid[row][col] > 0
• 1 <= k <= m * n

Metadata

• Link: K Highest Ranked Items Within a Price Range
• Difficulty: Medium
• Tag: Breadth-First Search Array Matrix Sorting Heap (Priority Queue)

You are given a 0-indexed 2D integer array grid of size m x n that represents a map of the items in a shop. The integers in the grid represent the following:

• 0 represents a wall that you cannot pass through.
• 1 represents an empty cell that you can freely move to and from.
• All other positive integers represent the price of an item in that cell. You may also freely move to and from these item cells.

It takes 1 step to travel between adjacent grid cells.

You are also given integer arrays pricing and start where pricing = [low, high] and start = [row, col] indicates that you start at the position (row, col) and are interested only in items with a price in the range of [low, high] (inclusive). You are further given an integer k.

You are interested in the positions of the k highest-ranked items whose prices are within the given price range. The rank is determined by the first of these criteria that is different:

1. Distance, defined as the length of the shortest path from the start (shorter distance has a higher rank).
2. Price (lower price has a higher rank, but it must be in the price range).
3. The row number (smaller row number has a higher rank).
4. The column number (smaller column number has a higher rank).

Return the k highest-ranked items within the price range sorted by their rank (highest to lowest). If there are fewer than k reachable items within the price range, return all of them.

 

Example 1:

Input: grid = [[1,2,0,1],[1,3,0,1],[0,2,5,1]], pricing = [2,5], start = [0,0], k = 3
Output: [[0,1],[1,1],[2,1]]
Explanation: You start at (0,0).
With a price range of [2,5], we can take items from (0,1), (1,1), (2,1) and (2,2).
The ranks of these items are:
- (0,1) with distance 1
- (1,1) with distance 2
- (2,1) with distance 3
- (2,2) with distance 4
Thus, the 3 highest ranked items in the price range are (0,1), (1,1), and (2,1).

Example 2:

Input: grid = [[1,2,0,1],[1,3,3,1],[0,2,5,1]], pricing = [2,3], start = [2,3], k = 2
Output: [[2,1],[1,2]]
Explanation: You start at (2,3).
With a price range of [2,3], we can take items from (0,1), (1,1), (1,2) and (2,1).
The ranks of these items are:
- (2,1) with distance 2, price 2
- (1,2) with distance 2, price 3
- (1,1) with distance 3
- (0,1) with distance 4
Thus, the 2 highest ranked items in the price range are (2,1) and (1,2).

Example 3:

Input: grid = [[1,1,1],[0,0,1],[2,3,4]], pricing = [2,3], start = [0,0], k = 3
Output: [[2,1],[2,0]]
Explanation: You start at (0,0).
With a price range of [2,3], we can take items from (2,0) and (2,1). 
The ranks of these items are: 
- (2,1) with distance 5
- (2,0) with distance 6
Thus, the 2 highest ranked items in the price range are (2,1) and (2,0). 
Note that k = 3 but there are only 2 reachable items within the price range.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 0 <= grid[i][j] <= 105
• pricing.length == 2
• 2 <= low <= high <= 105
• start.length == 2
• 0 <= row <= m - 1
• 0 <= col <= n - 1
• grid[row][col] > 0
• 1 <= k <= m * n

Solution

C++

#include <bits/stdc++.h>

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif

using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define Mkp make_pair
#define All(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
// head

struct node {
    int x, y, w, price;

    bool operator<(const node& other) const {
        if (w != other.w) {
            return w > other.w;
        }

        if (price != other.price) {
            return price > other.price;
        }

        if (x != other.x) {
            return x > other.x;
        }

        return y > other.y;
    }
};

int dir[4][2] = {
        {0, 1},
        {0, -1},
        {1, 0},
        {-1, 0},
};

class Solution {
public:
    vector<vector<int>> highestRankedKItems(
            vector<vector<int>>& grid, vector<int>& pricing, vector<int>& start, int k) {
        int n = grid.size();
        int m = grid[0].size();

        int sx = start[0], sy = start[1];

        priority_queue<node> pq;
        pq.push({sx, sy, 0, grid[sx][sy]});

        vector<vector<int>> vis(n, vector<int>(m, 0));
        vector<vector<int>> res;

        vis[sx][sy] = 1;

        while (!pq.empty() && res.size() < k) {
            node t = pq.top();
            pq.pop();

            if (t.price >= pricing[0] && t.price <= pricing[1]) {
                res.emplace_back(vector<int>{t.x, t.y});
            }

            for (int i = 0; i < 4; i++) {
                int nx = t.x + dir[i][0];
                int ny = t.y + dir[i][1];
                if (nx < 0 || nx >= n || ny < 0 || ny >= m) {
                    continue;
                }

                if (vis[nx][ny] == 1) {
                    continue;
                }

                vis[nx][ny] = 1;
                if (grid[nx][ny] == 0) {
                    continue;
                }

                pq.push({nx, ny, t.w + 1, grid[nx][ny]});
            }
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

D

Statement

简体中文English

Metadata

• Link: 分隔长廊的方案数
• Difficulty: Hard
• Tag: 数学 字符串 动态规划

在一个图书馆的长廊里，有一些座位和装饰植物排成一列。给你一个下标从 0 开始，长度为 n 的字符串 corridor ，它包含字母 'S' 和 'P' ，其中每个 'S' 表示一个座位，每个 'P' 表示一株植物。

在下标 0 的左边和下标 n - 1 的右边 已经 分别各放了一个屏风。你还需要额外放置一些屏风。每一个位置 i - 1 和 i 之间（1 <= i <= n - 1），至多能放一个屏风。

请你将走廊用屏风划分为若干段，且每一段内都 恰好有两个座位 ，而每一段内植物的数目没有要求。可能有多种划分方案，如果两个方案中有任何一个屏风的位置不同，那么它们被视为 不同 方案。

请你返回划分走廊的方案数。由于答案可能很大，请你返回它对 109 + 7 取余 的结果。如果没有任何方案，请返回 0 。

 

示例 1：

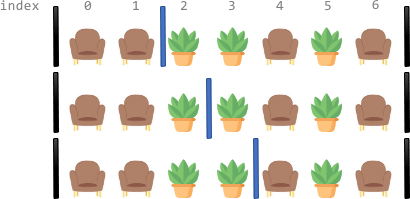
输入：corridor = "SSPPSPS"
输出：3
解释：总共有 3 种不同分隔走廊的方案。
上图中黑色的竖线表示已经放置好的屏风。
上图每种方案中，每一段都恰好有 两个 座位。

示例 2：

输入：corridor = "PPSPSP"
输出：1
解释：只有 1 种分隔走廊的方案，就是不放置任何屏风。
放置任何的屏风都会导致有一段无法恰好有 2 个座位。

示例 3：

输入：corridor = "S"
输出：0
解释：没有任何方案，因为总是有一段无法恰好有 2 个座位。

 

提示：

• n == corridor.length
• 1 <= n <= 105
• corridor[i] 要么是 'S' ，要么是 'P' 。

Metadata

• Link: Number of Ways to Divide a Long Corridor
• Difficulty: Hard
• Tag: Math String Dynamic Programming

Along a long library corridor, there is a line of seats and decorative plants. You are given a 0-indexed string corridor of length n consisting of letters 'S' and 'P' where each 'S' represents a seat and each 'P' represents a plant.

One room divider has already been installed to the left of index 0, and another to the right of index n - 1. Additional room dividers can be installed. For each position between indices i - 1 and i (1 <= i <= n - 1), at most one divider can be installed.

Divide the corridor into non-overlapping sections, where each section has exactly two seats with any number of plants. There may be multiple ways to perform the division. Two ways are different if there is a position with a room divider installed in the first way but not in the second way.

Return the number of ways to divide the corridor. Since the answer may be very large, return it modulo 109 + 7. If there is no way, return 0.

 

Example 1:

Input: corridor = "SSPPSPS"
Output: 3
Explanation: There are 3 different ways to divide the corridor.
The black bars in the above image indicate the two room dividers already installed.
Note that in each of the ways, each section has exactly two seats.

Example 2:

Input: corridor = "PPSPSP"
Output: 1
Explanation: There is only 1 way to divide the corridor, by not installing any additional dividers.
Installing any would create some section that does not have exactly two seats.

Example 3:

Input: corridor = "S"
Output: 0
Explanation: There is no way to divide the corridor because there will always be a section that does not have exactly two seats.

 

Constraints:

• n == corridor.length
• 1 <= n <= 105
• corridor[i] is either 'S' or 'P'.

Solution

C++

#include <bits/stdc++.h>

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif

using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define Mkp make_pair
#define All(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
// head

const int mod = 1e9 + 7;

class Solution {
public:
    int numberOfWays(string corridor) {
        ll res = 1;
        vector<int> v;

        int len = corridor.size();
        for (int i = 0; i < len; i++) {
            if (corridor[i] == 'S') {
                v.push_back(i);
            }
        }

        if (v.empty()) {
            return 0;
        }

        if (v.size() % 2) {
            return 0;
        }

        for (int i = 2; i < v.size(); i += 2) {
            res *= (v[i] - v[i - 1]);
            res %= mod;
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

---

最后更新: October 11, 2023