跳转至

biweekly-contest-86

A

Statement

Metadata

给你一个下标从 0 开始的整数数组 nums ，判断是否存在 两个 长度为 2 的子数组且它们的 和 相等。注意，这两个子数组起始位置的下标必须 不相同 。

如果这样的子数组存在，请返回 true，否则返回 false 。

子数组 是一个数组中一段连续非空的元素组成的序列。

 

示例 1：

输入：nums = [4,2,4]
输出：true
解释：元素为 [4,2] 和 [2,4] 的子数组有相同的和 6 。

示例 2：

输入：nums = [1,2,3,4,5]
输出：false
解释：没有长度为 2 的两个子数组和相等。

示例 3：

输入：nums = [0,0,0]
输出：true
解释：子数组 [nums[0],nums[1]] 和 [nums[1],nums[2]] 的和相等，都为 0 。
注意即使子数组的元素相同，这两个子数组也视为不相同的子数组，因为它们在原数组中的起始位置不同。

 

提示：

  • 2 <= nums.length <= 1000
  • -109 <= nums[i] <= 109

Metadata

Given a 0-indexed integer array nums, determine whether there exist two subarrays of length 2 with equal sum. Note that the two subarrays must begin at different indices.

Return true if these subarrays exist, and false otherwise.

A subarray is a contiguous non-empty sequence of elements within an array.

 

Example 1:

Input: nums = [4,2,4]
Output: true
Explanation: The subarrays with elements [4,2] and [2,4] have the same sum of 6.

Example 2:

Input: nums = [1,2,3,4,5]
Output: false
Explanation: No two subarrays of size 2 have the same sum.

Example 3:

Input: nums = [0,0,0]
Output: true
Explanation: The subarrays [nums[0],nums[1]] and [nums[1],nums[2]] have the same sum of 0. 
Note that even though the subarrays have the same content, the two subarrays are considered different because they are in different positions in the original array.

 

Constraints:

  • 2 <= nums.length <= 1000
  • -109 <= nums[i] <= 109

Solution

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    bool findSubarrays(vector<int> &nums) {
        int n = int(nums.size());
        auto mp = std::map<int, int>();
        for (int i = 1; i < n; i++) {
            auto res = nums[i - 1] + nums[i];
            if (mp.count(res)) {
                return true;
            }

            mp[res] = 1;
        }

        return false;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

Metadata

如果一个整数 n 在 b 进制下（b 为 2 到 n - 2 之间的所有整数）对应的字符串 全部 都是 回文的 ，那么我们称这个数 n 是 严格回文 的。

给你一个整数 n ，如果 n 是 严格回文 的，请返回 true ，否则返回 false 。

如果一个字符串从前往后读和从后往前读完全相同，那么这个字符串是 回文的 。

 

示例 1：

输入：n = 9
输出：false
解释：在 2 进制下：9 = 1001 ，是回文的。
在 3 进制下：9 = 100 ，不是回文的。
所以，9 不是严格回文数字，我们返回 false 。
注意在 4, 5, 6 和 7 进制下，n = 9 都不是回文的。

示例 2：

输入：n = 4
输出：false
解释：我们只考虑 2 进制：4 = 100 ，不是回文的。
所以我们返回 false 。

 

提示：

  • 4 <= n <= 105

Metadata

An integer n is strictly palindromic if, for every base b between 2 and n - 2 (inclusive), the string representation of the integer n in base b is palindromic.

Given an integer n, return true if n is strictly palindromic and false otherwise.

A string is palindromic if it reads the same forward and backward.

 

Example 1:

Input: n = 9
Output: false
Explanation: In base 2: 9 = 1001 (base 2), which is palindromic.
In base 3: 9 = 100 (base 3), which is not palindromic.
Therefore, 9 is not strictly palindromic so we return false.
Note that in bases 4, 5, 6, and 7, n = 9 is also not palindromic.

Example 2:

Input: n = 4
Output: false
Explanation: We only consider base 2: 4 = 100 (base 2), which is not palindromic.
Therefore, we return false.

 

Constraints:

  • 4 <= n <= 105

Solution

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    bool isStrictlyPalindromic(int n) {
        auto ok = [_n = n](int b) -> bool {
            int n = _n;
            auto v = vector<int>();
            while (n) {
                v.push_back(n % b);
                n /= b;
            }

            auto _v = v;
            reverse(all(_v));
            return v == _v;
        };

        for (int i = 2; i <= n - 2; i++) {
            if (!ok(i)) {
                return false;
            }
        }

        return true;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

Metadata

给你一个下标从 0 开始的 m x n 二进制矩阵 mat 和一个整数 cols ，表示你需要选出的列数。

如果一行中，所有的 1 都被你选中的列所覆盖，那么我们称这一行 被覆盖 了。

请你返回在选择 cols 列的情况下，被覆盖 的行数 最大 为多少。

 

示例 1：

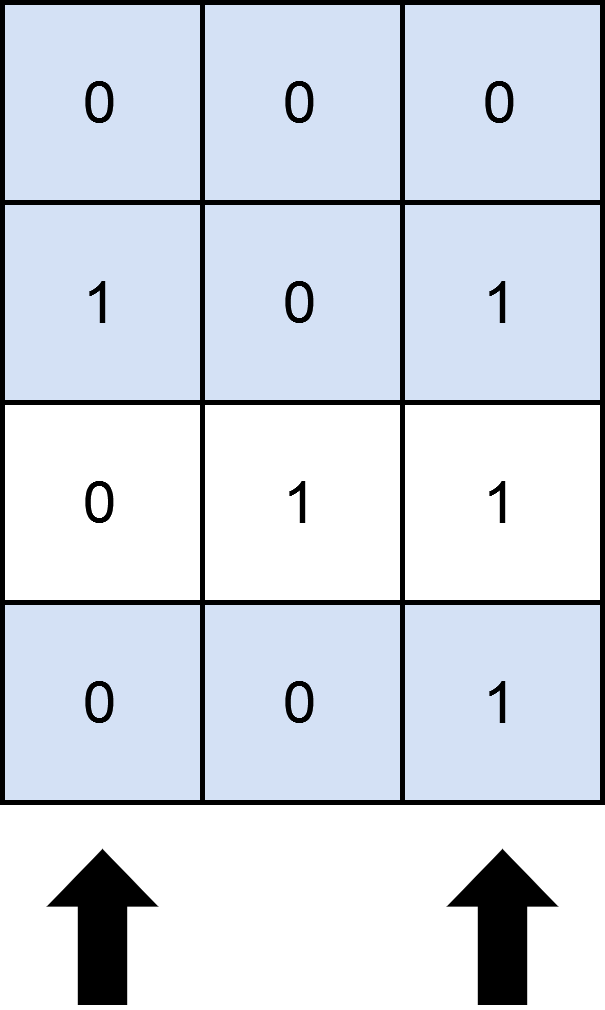
输入：mat = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], cols = 2
输出：3
解释：
如上图所示，覆盖 3 行的一种可行办法是选择第 0 和第 2 列。
可以看出，不存在大于 3 行被覆盖的方案，所以我们返回 3 。

示例 2：

输入：mat = [[1],[0]], cols = 1
输出：2
解释：
选择唯一的一列，两行都被覆盖了，原因是整个矩阵都被覆盖了。
所以我们返回 2 。

 

提示：

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 12
  • mat[i][j] 要么是 0 要么是 1 。
  • 1 <= cols <= n

Metadata

You are given a 0-indexed m x n binary matrix mat and an integer cols, which denotes the number of columns you must choose.

A row is covered by a set of columns if each cell in the row that has a value of 1 also lies in one of the columns of the chosen set.

Return the maximum number of rows that can be covered by a set of cols columns.

 

Example 1:

Input: mat = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], cols = 2
Output: 3
Explanation:
As shown in the diagram above, one possible way of covering 3 rows is by selecting the 0th and 2nd columns.
It can be shown that no more than 3 rows can be covered, so we return 3.

Example 2:

Input: mat = [[1],[0]], cols = 1
Output: 2
Explanation:
Selecting the only column will result in both rows being covered, since the entire matrix is selected.
Therefore, we return 2.

 

Constraints:

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 12
  • mat[i][j] is either 0 or 1.
  • 1 <= cols <= n

Solution

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    int maximumRows(vector<vector<int>> &mat, int cols) {
        int m = int(mat.size());
        int n = int(mat[0].size());
        auto v = vector<int>();
        for (int i = 0; i < m; i++) {
            int res = 0;
            for (int j = 0; j < n; j++) {
                res = (res << 1) + mat[i][j];
            }
            v.push_back(res);
        }
        int res = 0;
        for (int S = 0; S < (1 << n); ++S) {
            if (__builtin_popcount(S) > cols) {
                continue;
            }

            int _res = 0;
            for (int i = 0; i < m; i++) {
                _res += (((v[i] ^ S) & v[i]) == 0);
            }

            res = max(res, _res);
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

D

Statement

Metadata

你有 n 个机器人，给你两个下标从 0 开始的整数数组 chargeTimes 和 runningCosts ，两者长度都为 n 。第 i 个机器人充电时间为 chargeTimes[i] 单位时间，花费 runningCosts[i] 单位时间运行。再给你一个整数 budget 。

运行 k 个机器人 总开销 是 max(chargeTimes) + k * sum(runningCosts) ，其中 max(chargeTimes) 是这 k 个机器人中最大充电时间，sum(runningCosts) 是这 k 个机器人的运行时间之和。

请你返回在 不超过 budget 的前提下，你 最多 可以 连续 运行的机器人数目为多少。

 

示例 1：

输入：chargeTimes = [3,6,1,3,4], runningCosts = [2,1,3,4,5], budget = 25
输出：3
解释：
可以在 budget 以内运行所有单个机器人或者连续运行 2 个机器人。
选择前 3 个机器人，可以得到答案最大值 3 。总开销是 max(3,6,1) + 3 * sum(2,1,3) = 6 + 3 * 6 = 24 ，小于 25 。
可以看出无法在 budget 以内连续运行超过 3 个机器人，所以我们返回 3 。

示例 2：

输入：chargeTimes = [11,12,19], runningCosts = [10,8,7], budget = 19
输出：0
解释：即使运行任何一个单个机器人，还是会超出 budget，所以我们返回 0 。

 

提示：

  • chargeTimes.length == runningCosts.length == n
  • 1 <= n <= 5 * 104
  • 1 <= chargeTimes[i], runningCosts[i] <= 105
  • 1 <= budget <= 1015

Metadata

You have n robots. You are given two 0-indexed integer arrays, chargeTimes and runningCosts, both of length n. The ith robot costs chargeTimes[i] units to charge and costs runningCosts[i] units to run. You are also given an integer budget.

The total cost of running k chosen robots is equal to max(chargeTimes) + k * sum(runningCosts), where max(chargeTimes) is the largest charge cost among the k robots and sum(runningCosts) is the sum of running costs among the k robots.

Return the maximum number of consecutive robots you can run such that the total cost does not exceed budget.

 

Example 1:

Input: chargeTimes = [3,6,1,3,4], runningCosts = [2,1,3,4,5], budget = 25
Output: 3
Explanation: 
It is possible to run all individual and consecutive pairs of robots within budget.
To obtain answer 3, consider the first 3 robots. The total cost will be max(3,6,1) + 3 * sum(2,1,3) = 6 + 3 * 6 = 24 which is less than 25.
It can be shown that it is not possible to run more than 3 consecutive robots within budget, so we return 3.

Example 2:

Input: chargeTimes = [11,12,19], runningCosts = [10,8,7], budget = 19
Output: 0
Explanation: No robot can be run that does not exceed the budget, so we return 0.

 

Constraints:

  • chargeTimes.length == runningCosts.length == n
  • 1 <= n <= 5 * 104
  • 1 <= chargeTimes[i], runningCosts[i] <= 105
  • 1 <= budget <= 1015

Solution

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    int maximumRobots(vector<int> &c, vector<int> &r, long long b) {
        int n = int(c.size());

        auto s = vector<ll>(n + 5, 0);
        auto cc = vector<pair<int, int>>();

        int res = 0;

        for (int i = 0; i < n; i++) {
            s[i + 1] = s[i] + r[i];
            auto _c = make_pair(i, c[i]);
            while (!cc.empty()) {
                if (cc.back().second <= _c.second) {
                    cc.pop_back();
                } else {
                    break;
                }
            }
            cc.push_back(_c);

            int l = 1, r = (i + 1), _res = 0;
            while (r - l >= 0) {
                int mid = (l + r) >> 1;

                ll sum = s[i + 1] - s[i + 1 - mid];
                int cnt = mid;
                auto pos = upper_bound(all(cc), make_pair(i - mid + 1, -1));
                // auto pos = cc.begin();

                // 5 8 9 1

                if (sum * cnt + pos->second <= b) {
                    l = mid + 1;
                    _res = mid;
                } else {
                    r = mid - 1;
                }
            }

            res = max(res, _res);
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif
最后更新: October 11, 2023
回到页面顶部