biweekly-contest-76

A

Statement

简体中文English

Metadata

Link: 找到最接近 0 的数字
Difficulty: Easy
Tag:

给你一个长度为 n 的整数数组 nums ，请你返回 nums 中最接近 0 的数字。如果有多个答案，请你返回它们中的 最大值 。

示例 1：

输入：nums = [-4,-2,1,4,8]
输出：1
解释：
-4 到 0 的距离为 |-4| = 4 。
-2 到 0 的距离为 |-2| = 2 。
1 到 0 的距离为 |1| = 1 。
4 到 0 的距离为 |4| = 4 。
8 到 0 的距离为 |8| = 8 。
所以，数组中距离 0 最近的数字为 1 。

示例 2：

输入：nums = [2,-1,1]
输出：1
解释：1 和 -1 都是距离 0 最近的数字，所以返回较大值 1 。

提示：

1 <= n <= 1000
-10⁵ <= nums[i] <= 10⁵

Metadata

Link: Find Closest Number to Zero
Difficulty: Easy
Tag:

Given an integer array nums of size n, return the number with the value closest to 0 in nums. If there are multiple answers, return the number with the largest value.

Example 1:

Input: nums = [-4,-2,1,4,8]
Output: 1
Explanation:
The distance from -4 to 0 is |-4| = 4.
The distance from -2 to 0 is |-2| = 2.
The distance from 1 to 0 is |1| = 1.
The distance from 4 to 0 is |4| = 4.
The distance from 8 to 0 is |8| = 8.
Thus, the closest number to 0 in the array is 1.

Example 2:

Input: nums = [2,-1,1]
Output: 1
Explanation: 1 and -1 are both the closest numbers to 0, so 1 being larger is returned.

Constraints:

1 <= n <= 1000
-10⁵ <= nums[i] <= 10⁵

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    int findClosestNumber(vector<int> &nums) {
        int a = 0x3f3f3f3f;
        int b = 0;
        for (auto &aa : nums) {
            int x = abs(aa);
            if (x < a) {
                a = x;
                b = aa;
            } else if (x == a) {
                b = max(b, aa);
            }
        }

        return b;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

简体中文English

Metadata

Link: 买钢笔和铅笔的方案数
Difficulty: Medium
Tag:

给你一个整数 total ，表示你拥有的总钱数。同时给你两个整数 cost1 和 cost2 ，分别表示一支钢笔和一支铅笔的价格。你可以花费你部分或者全部的钱，去买任意数目的两种笔。

请你返回购买钢笔和铅笔的 不同方案数目 。

示例 1：

输入：total = 20, cost1 = 10, cost2 = 5
输出：9
解释：一支钢笔的价格为 10 ，一支铅笔的价格为 5 。
- 如果你买 0 支钢笔，那么你可以买 0 ，1 ，2 ，3 或者 4 支铅笔。
- 如果你买 1 支钢笔，那么你可以买 0 ，1 或者 2 支铅笔。
- 如果你买 2 支钢笔，那么你没法买任何铅笔。
所以买钢笔和铅笔的总方案数为 5 + 3 + 1 = 9 种。

示例 2：

输入：total = 5, cost1 = 10, cost2 = 10
输出：1
解释：钢笔和铅笔的价格都为 10 ，都比拥有的钱数多，所以你没法购买任何文具。所以只有 1 种方案：买 0 支钢笔和 0 支铅笔。

提示：

1 <= total, cost1, cost2 <= 10⁶

Metadata

Link: Number of Ways to Buy Pens and Pencils
Difficulty: Medium
Tag:

You are given an integer total indicating the amount of money you have. You are also given two integers cost1 and cost2 indicating the price of a pen and pencil respectively. You can spend part or all of your money to buy multiple quantities (or none) of each kind of writing utensil.

Return the number of distinct ways you can buy some number of pens and pencils.

Example 1:

Input: total = 20, cost1 = 10, cost2 = 5
Output: 9
Explanation: The price of a pen is 10 and the price of a pencil is 5.
- If you buy 0 pens, you can buy 0, 1, 2, 3, or 4 pencils.
- If you buy 1 pen, you can buy 0, 1, or 2 pencils.
- If you buy 2 pens, you cannot buy any pencils.
The total number of ways to buy pens and pencils is 5 + 3 + 1 = 9.

Example 2:

Input: total = 5, cost1 = 10, cost2 = 10
Output: 1
Explanation: The price of both pens and pencils are 10, which cost more than total, so you cannot buy any writing utensils. Therefore, there is only 1 way: buy 0 pens and 0 pencils.

Constraints:

1 <= total, cost1, cost2 <= 10⁶

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    long long waysToBuyPensPencils(int total, int cost1, int cost2) {
        ll res = 0;
        for (int i = 0; i <= total / cost1; i++) {
            res += (total - cost1 * i) / cost2 + 1;
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

简体中文English

Metadata

Link: 设计一个 ATM 机器
Difficulty: Medium
Tag:

一个 ATM 机器，存有 5 种面值的钞票：20 ，50 ，100 ，200 和 500 美元。初始时，ATM 机是空的。用户可以用它存或者取任意数目的钱。

取款时，机器会优先取较大数额的钱。

比方说，你想取 $300 ，并且机器里有 2 张 $50 的钞票，1 张 $100 的钞票和1 张 $200 的钞票，那么机器会取出 $100 和 $200 的钞票。
但是，如果你想取 $600 ，机器里有 3 张 $200 的钞票和1 张 $500 的钞票，那么取款请求会被拒绝，因为机器会先取出 $500 的钞票，然后无法取出剩余的 $100 。注意，因为有 $500 钞票的存在，机器不能取 $200 的钞票。

请你实现 ATM 类：

ATM() 初始化 ATM 对象。
void deposit(int[] banknotesCount) 分别存入 $20 ，$50，$100，$200 和 $500 钞票的数目。
int[] withdraw(int amount) 返回一个长度为 5 的数组，分别表示 $20 ，$50，$100 ，$200 和 $500 钞票的数目，并且更新 ATM 机里取款后钞票的剩余数量。如果无法取出指定数额的钱，请返回 [-1] （这种情况下不取出任何钞票）。

示例 1：

输入：
["ATM", "deposit", "withdraw", "deposit", "withdraw", "withdraw"]
[[], [[0,0,1,2,1]], [600], [[0,1,0,1,1]], [600], [550]]
输出：
[null, null, [0,0,1,0,1], null, [-1], [0,1,0,0,1]]
解释：
ATM atm = new ATM();
atm.deposit([0,0,1,2,1]); // 存入 1 张 $100 ，2 张 $200 和 1 张 $500 的钞票。
atm.withdraw(600);        // 返回 [0,0,1,0,1] 。机器返回 1 张 $100 和 1 张 $500 的钞票。机器里剩余钞票的数量为 [0,0,0,2,0] 。
atm.deposit([0,1,0,1,1]); // 存入 1 张 $50 ，1 张 $200 和 1 张 $500 的钞票。
                          // 机器中剩余钞票数量为 [0,1,0,3,1] 。
atm.withdraw(600);        // 返回 [-1] 。机器会尝试取出 $500 的钞票，然后无法得到剩余的 $100 ，所以取款请求会被拒绝。
                          // 由于请求被拒绝，机器中钞票的数量不会发生改变。
atm.withdraw(550);        // 返回 [0,1,0,0,1] ，机器会返回 1 张 $50 的钞票和 1 张 $500 的钞票。

提示：

banknotesCount.length == 5
0 <= banknotesCount[i] <= 10⁹
1 <= amount <= 10⁹
总共最多有 5000 次 withdraw 和 deposit 的调用。
函数 withdraw 和 deposit 至少各有一次调用。

Metadata

Link: Design an ATM Machine
Difficulty: Medium
Tag:

There is an ATM machine that stores banknotes of 5 denominations: 20, 50, 100, 200, and 500 dollars. Initially the ATM is empty. The user can use the machine to deposit or withdraw any amount of money.

When withdrawing, the machine prioritizes using banknotes of larger values.

For example, if you want to withdraw $300 and there are 2 $50 banknotes, 1 $100 banknote, and 1 $200 banknote, then the machine will use the $100 and $200 banknotes.
However, if you try to withdraw $600 and there are 3 $200 banknotes and 1 $500 banknote, then the withdraw request will be rejected because the machine will first try to use the $500 banknote and then be unable to use banknotes to complete the remaining $100. Note that the machine is not allowed to use the $200 banknotes instead of the $500 banknote.

Implement the ATM class:

ATM() Initializes the ATM object.
void deposit(int[] banknotesCount) Deposits new banknotes in the order $20, $50, $100, $200, and $500.
int[] withdraw(int amount) Returns an array of length 5 of the number of banknotes that will be handed to the user in the order $20, $50, $100, $200, and $500, and update the number of banknotes in the ATM after withdrawing. Returns [-1] if it is not possible (do not withdraw any banknotes in this case).

Example 1:

Input
["ATM", "deposit", "withdraw", "deposit", "withdraw", "withdraw"]
[[], [[0,0,1,2,1]], [600], [[0,1,0,1,1]], [600], [550]]
Output
[null, null, [0,0,1,0,1], null, [-1], [0,1,0,0,1]]
Explanation
ATM atm = new ATM();
atm.deposit([0,0,1,2,1]); // Deposits 1 $100 banknote, 2 $200 banknotes,
                          // and 1 $500 banknote.
atm.withdraw(600);        // Returns [0,0,1,0,1]. The machine uses 1 $100 banknote
                          // and 1 $500 banknote. The banknotes left over in the
                          // machine are [0,0,0,2,0].
atm.deposit([0,1,0,1,1]); // Deposits 1 $50, $200, and $500 banknote.
                          // The banknotes in the machine are now [0,1,0,3,1].
atm.withdraw(600);        // Returns [-1]. The machine will try to use a $500 banknote
                          // and then be unable to complete the remaining $100,
                          // so the withdraw request will be rejected.
                          // Since the request is rejected, the number of banknotes
                          // in the machine is not modified.
atm.withdraw(550);        // Returns [0,1,0,0,1]. The machine uses 1 $50 banknote
                          // and 1 $500 banknote.

Constraints:

banknotesCount.length == 5
0 <= banknotesCount[i] <= 10⁹
1 <= amount <= 10⁹
At most 5000 calls in total will be made to withdraw and deposit.
At least one call will be made to each function withdraw and deposit.

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;

template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class ATM {
public:
    vector<ll> v;
    vector<int> f;
    ATM() {
        v = vector<ll>(10, 0);
        f = vector<int>({20, 50, 100, 200, 500});
    }

    void deposit(vector<int> banknotesCount) {
        for (int i = 0; i < 5; i++) {
            v[i] += banknotesCount[i];
        }
    }

    vector<int> withdraw(int amount) {
        auto res = vector<int>(5, 0);
        int remind = amount;
        for (int i = 4; i >= 0; i--) {
            ll cur = min<ll>(v[i], remind / f[i]);
            res[i] = cur;
            remind -= f[i] * cur;
        }

        if (remind != 0) {
            return vector<int>({-1});
        }

        for (int i = 0; i < 5; i++) {
            v[i] -= res[i];
        }

        return res;
    }
};

/**
 * Your ATM object will be instantiated and called as such:
 * ATM* obj = new ATM();
 * obj->deposit(banknotesCount);
 * vector<int> param_2 = obj->withdraw(amount);
 */

#ifdef LOCAL

int main() {
    return 0;
}

#endif

D

Statement

简体中文English

Metadata

Link: 节点序列的最大得分
Difficulty: Hard
Tag:

给你一个 n 个节点的 无向图 ，节点编号为 0 到 n - 1 。

给你一个下标从 0 开始的整数数组 scores ，其中 scores[i] 是第 i 个节点的分数。同时给你一个二维整数数组 edges ，其中 edges[i] = [a_i, b_i] ，表示节点 a_i 和 b_i 之间有一条无向边。

一个合法的节点序列如果满足以下条件，我们称它是 合法的 ：

序列中每相邻节点之间有边相连。
序列中没有节点出现超过一次。

节点序列的分数定义为序列中节点分数之和。

请你返回一个长度为 4 的合法节点序列的最大分数。如果不存在这样的序列，请你返回 -1 。

示例 1：

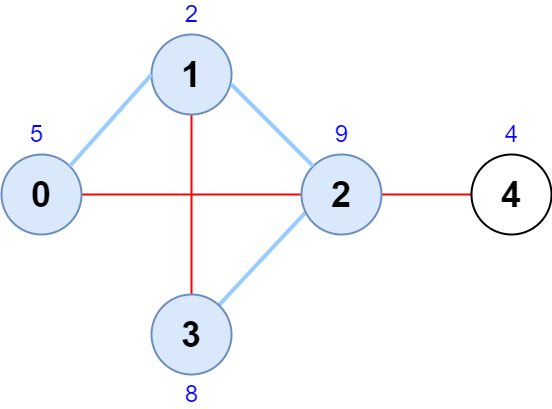
输入：scores = [5,2,9,8,4], edges = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
输出：24
解释：上图为输入的图，节点序列为 [0,1,2,3] 。
节点序列的分数为 5 + 2 + 9 + 8 = 24 。
观察可知，没有其他节点序列得分和超过 24 。
注意节点序列 [3,1,2,0] 和 [1,0,2,3] 也是合法的，且分数为 24 。
序列 [0,3,2,4] 不是合法的，因为没有边连接节点 0 和 3 。

示例 2：

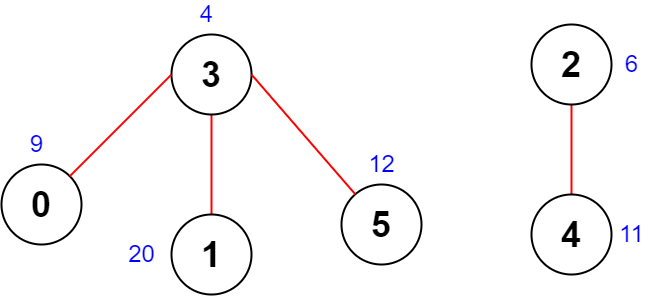
输入：scores = [9,20,6,4,11,12], edges = [[0,3],[5,3],[2,4],[1,3]]
输出：-1
解释：上图为输入的图。
没有长度为 4 的合法序列，所以我们返回 -1 。

提示：

n == scores.length
4 <= n <= 5 * 10⁴
1 <= scores[i] <= 10⁸
0 <= edges.length <= 5 * 10⁴
edges[i].length == 2
0 <= a_i, b_i <= n - 1
a_i != b_i
不会有重边。

Metadata

Link: Maximum Score of a Node Sequence
Difficulty: Hard
Tag:

There is an undirected graph with n nodes, numbered from 0 to n - 1.

You are given a 0-indexed integer array scores of length n where scores[i] denotes the score of node i. You are also given a 2D integer array edges where edges[i] = [a_i, b_i] denotes that there exists an undirected edge connecting nodes a_i and b_i.

A node sequence is valid if it meets the following conditions:

There is an edge connecting every pair of adjacent nodes in the sequence.
No node appears more than once in the sequence.

The score of a node sequence is defined as the sum of the scores of the nodes in the sequence.

Return the maximum score of a valid node sequence with a length of 4. If no such sequence exists, return -1.

Example 1:

Input: scores = [5,2,9,8,4], edges = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
Output: 24
Explanation: The figure above shows the graph and the chosen node sequence [0,1,2,3].
The score of the node sequence is 5 + 2 + 9 + 8 = 24.
It can be shown that no other node sequence has a score of more than 24.
Note that the sequences [3,1,2,0] and [1,0,2,3] are also valid and have a score of 24.
The sequence [0,3,2,4] is not valid since no edge connects nodes 0 and 3.

Example 2:

Input: scores = [9,20,6,4,11,12], edges = [[0,3],[5,3],[2,4],[1,3]]
Output: -1
Explanation: The figure above shows the graph.
There are no valid node sequences of length 4, so we return -1.

Constraints:

n == scores.length
4 <= n <= 5 * 10⁴
1 <= scores[i] <= 10⁸
0 <= edges.length <= 5 * 10⁴
edges[i].length == 2
0 <= a_i, b_i <= n - 1
a_i != b_i
There are no duplicate edges.

Solution

C++

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;

template <typename T, typename S>
inline bool chmax(T& a, const S& b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T& a, const S& b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

const int INF = 0x3f3f3f3f;

class Solution {
public:
    int maximumScore(vector<int>& scores, vector<vector<int>>& edges) {
        int n = scores.size();

        auto f = vector<vector<PII>>(n + 1, vector<PII>(3, PII(-1, -INF)));
        auto G = vector<vector<int>>(n + 1, vector<int>());

        for (const auto& e : edges) {
            int u = e[0];
            int v = e[1];

            G[v].push_back(u);
            G[u].push_back(v);
        }

        for (int u = 0; u < n; u++) {
            for (const auto& v : G[u]) {
                int s = scores[v];

                for (int i = 0; i < 3; i++) {
                    if (s > f[u][i].second) {
                        for (int j = 2; j > i; j--) {
                            f[u][j] = f[u][j - 1];
                        }

                        f[u][i] = PII(v, s);
                        break;
                    }
                }
            }
        }

        int res = -1;

        for (int u = 0; u < n; u++) {
            int su = scores[u];

            for (const auto& v : G[u]) {
                int sv = scores[v];

                for (int i = 0; i < 3; i++) {
                    int uu = f[u][i].first;
                    if (uu == -1) {
                        break;
                    }

                    if (uu == v) {
                        continue;
                    }

                    for (int j = 0; j < 3; j++) {
                        int vv = f[v][j].first;
                        if (vv == -1) {
                            break;
                        }

                        if (vv == uu || vv == u) {
                            continue;
                        }

                        int now = su + sv + f[u][i].second + f[v][j].second;

                        res = max(res, now);
                    }
                }
            }
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

最后更新: October 11, 2023