weekly-contest-328
A
Statement
Metadata
- Link: 数组元素和与数字和的绝对差
- Difficulty: Easy
- Tag:
给你一个正整数数组 nums 。
- 元素和 是
nums中的所有元素相加求和。 - 数字和 是
nums中每一个元素的每一数位(重复数位需多次求和)相加求和。
返回 元素和 与 数字和 的绝对差。
注意:两个整数 x 和 y 的绝对差定义为 |x - y| 。
示例 1:
输入:nums = [1,15,6,3]
输出:9
解释:
nums 的元素和是 1 + 15 + 6 + 3 = 25 。
nums 的数字和是 1 + 1 + 5 + 6 + 3 = 16 。
元素和与数字和的绝对差是 |25 - 16| = 9 。
示例 2:
输入:nums = [1,2,3,4]
输出:0
解释:
nums 的元素和是 1 + 2 + 3 + 4 = 10 。
nums 的数字和是 1 + 2 + 3 + 4 = 10 。
元素和与数字和的绝对差是 |10 - 10| = 0 。
提示:
1 <= nums.length <= 20001 <= nums[i] <= 2000
Metadata
- Link: Difference Between Element Sum and Digit Sum of an Array
- Difficulty: Easy
- Tag:
You are given a positive integer array nums.
- The element sum is the sum of all the elements in
nums. - The digit sum is the sum of all the digits (not necessarily distinct) that appear in
nums.
Return the absolute difference between the element sum and digit sum of nums.
Note that the absolute difference between two integers x and y is defined as |x - y|.
Example 1:
Input: nums = [1,15,6,3]
Output: 9
Explanation:
The element sum of nums is 1 + 15 + 6 + 3 = 25.
The digit sum of nums is 1 + 1 + 5 + 6 + 3 = 16.
The absolute difference between the element sum and digit sum is |25 - 16| = 9.
Example 2:
Input: nums = [1,2,3,4]
Output: 0
Explanation:
The element sum of nums is 1 + 2 + 3 + 4 = 10.
The digit sum of nums is 1 + 2 + 3 + 4 = 10.
The absolute difference between the element sum and digit sum is |10 - 10| = 0.
Constraints:
1 <= nums.length <= 20001 <= nums[i] <= 2000
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int differenceOfSum(vector<int> &nums) {
int tot = 0;
int sum = 0;
for (int a : nums) {
tot += a;
while (a) {
sum += a % 10;
a /= 10;
}
}
return abs(tot - sum);
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 子矩阵元素加 1
- Difficulty: Medium
- Tag:
给你一个正整数 n ,表示最初有一个 n x n 、下标从 0 开始的整数矩阵 mat ,矩阵中填满了 0 。
另给你一个二维整数数组 query 。针对每个查询 query[i] = [row1i, col1i, row2i, col2i] ,请你执行下述操作:
- 找出 左上角 为
(row1i, col1i)且 右下角 为(row2i, col2i)的子矩阵,将子矩阵中的 每个元素 加1。也就是给所有满足row1i <= x <= row2i和col1i <= y <= col2i的mat[x][y]加1。
返回执行完所有操作后得到的矩阵 mat 。
示例 1:
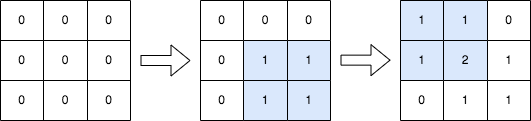
输入:n = 3, queries = [[1,1,2,2],[0,0,1,1]]
输出:[[1,1,0],[1,2,1],[0,1,1]]
解释:上图所展示的分别是:初始矩阵、执行完第一个操作后的矩阵、执行完第二个操作后的矩阵。
- 第一个操作:将左上角为 (1, 1) 且右下角为 (2, 2) 的子矩阵中的每个元素加 1 。
- 第二个操作:将左上角为 (0, 0) 且右下角为 (1, 1) 的子矩阵中的每个元素加 1 。
示例 2:

输入:n = 2, queries = [[0,0,1,1]]
输出:[[1,1],[1,1]]
解释:上图所展示的分别是:初始矩阵、执行完第一个操作后的矩阵。
- 第一个操作:将矩阵中的每个元素加 1 。
提示:
1 <= n <= 5001 <= queries.length <= 1040 <= row1i <= row2i < n0 <= col1i <= col2i < n
Metadata
- Link: Increment Submatrices by One
- Difficulty: Medium
- Tag:
You are given a positive integer n, indicating that we initially have an n x n 0-indexed integer matrix mat filled with zeroes.
You are also given a 2D integer array query. For each query[i] = [row1i, col1i, row2i, col2i], you should do the following operation:
- Add
1to every element in the submatrix with the top left corner(row1i, col1i)and the bottom right corner(row2i, col2i). That is, add1tomat[x][y]for for allrow1i <= x <= row2iandcol1i <= y <= col2i.
Return the matrix mat after performing every query.
Example 1:

Input: n = 3, queries = [[1,1,2,2],[0,0,1,1]]
Output: [[1,1,0],[1,2,1],[0,1,1]]
Explanation: The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
Example 2:

Input: n = 2, queries = [[0,0,1,1]]
Output: [[1,1],[1,1]]
Explanation: The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.
Constraints:
1 <= n <= 5001 <= queries.length <= 1040 <= row1i <= row2i < n0 <= col1i <= col2i < n
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
vector<vector<int>> rangeAddQueries(int n, vector<vector<int>> &queries) {
auto f = vector<vector<int>>(n + 5, vector<int>(n + 5, 0));
for (const auto &q : queries) {
int x1 = q[0] + 1;
int y1 = q[1] + 1;
int x2 = q[2] + 1;
int y2 = q[3] + 1;
++f[x1][y1];
--f[x1][y2 + 1];
--f[x2 + 1][y1];
++f[x2 + 1][y2 + 1];
}
auto res = vector<vector<int>>(n, vector<int>(n, 0));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (i) {
f[i][j] += f[i - 1][j];
}
if (j) {
f[i][j] += f[i][j - 1];
}
if (i && j) {
f[i][j] -= f[i - 1][j - 1];
}
res[i - 1][j - 1] = f[i][j];
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 统计好子数组的数目
- Difficulty: Medium
- Tag:
给你一个整数数组 nums 和一个整数 k ,请你返回 nums 中 好 子数组的数目。
一个子数组 arr 如果有 至少 k 对下标 (i, j) 满足 i < j 且 arr[i] == arr[j] ,那么称它是一个 好 子数组。
子数组 是原数组中一段连续 非空 的元素序列。
示例 1:
输入:nums = [1,1,1,1,1], k = 10
输出:1
解释:唯一的好子数组是这个数组本身。
示例 2:
输入:nums = [3,1,4,3,2,2,4], k = 2
输出:4
解释:总共有 4 个不同的好子数组:
- [3,1,4,3,2,2] 有 2 对。
- [3,1,4,3,2,2,4] 有 3 对。
- [1,4,3,2,2,4] 有 2 对。
- [4,3,2,2,4] 有 2 对。
提示:
1 <= nums.length <= 1051 <= nums[i], k <= 109
Metadata
- Link: Count the Number of Good Subarrays
- Difficulty: Medium
- Tag:
Given an integer array nums and an integer k, return the number of good subarrays of nums.
A subarray arr is good if it there are at least k pairs of indices (i, j) such that i < j and arr[i] == arr[j].
A subarray is a contiguous non-empty sequence of elements within an array.
Example 1:
Input: nums = [1,1,1,1,1], k = 10
Output: 1
Explanation: The only good subarray is the array nums itself.
Example 2:
Input: nums = [3,1,4,3,2,2,4], k = 2
Output: 4
Explanation: There are 4 different good subarrays:
- [3,1,4,3,2,2] that has 2 pairs.
- [3,1,4,3,2,2,4] that has 3 pairs.
- [1,4,3,2,2,4] that has 2 pairs.
- [4,3,2,2,4] that has 2 pairs.
Constraints:
1 <= nums.length <= 1051 <= nums[i], k <= 109
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
ll calc(int x) {
return 1ll * x * (x - 1) / 2;
}
long long countGood(vector<int> &nums, int k) {
int n = int(nums.size());
auto mp = map<int, int>();
ll res = 0;
ll tot = 0;
int l = -1;
for (int i = 0; i < n; i++) {
int x = nums[i];
tot -= calc(mp[x]);
++mp[x];
tot += calc(mp[x]);
while (l < i) {
int y = nums[l + 1];
ll _tot = tot;
_tot -= calc(mp[y]);
_tot += calc(mp[y] - 1);
if (_tot >= k) {
++l;
--mp[y];
tot = _tot;
} else {
break;
}
}
if (tot >= k) {
res += (l + 2);
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 最大价值和与最小价值和的差值
- Difficulty: Hard
- Tag:
给你一个 n 个节点的无向无根图,节点编号为 0 到 n - 1 。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间有一条边。
每个节点都有一个价值。给你一个整数数组 price ,其中 price[i] 是第 i 个节点的价值。
一条路径的 价值和 是这条路径上所有节点的价值之和。
你可以选择树中任意一个节点作为根节点 root 。选择 root 为根的 开销 是以 root 为起点的所有路径中,价值和 最大的一条路径与最小的一条路径的差值。
请你返回所有节点作为根节点的选择中,最大 的 开销 为多少。
示例 1:
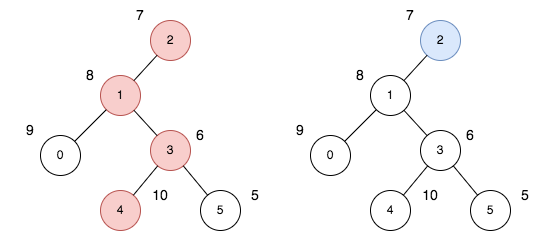
输入:n = 6, edges = [[0,1],[1,2],[1,3],[3,4],[3,5]], price = [9,8,7,6,10,5]
输出:24
解释:上图展示了以节点 2 为根的树。左图(红色的节点)是最大价值和路径,右图(蓝色的节点)是最小价值和路径。
- 第一条路径节点为 [2,1,3,4]:价值为 [7,8,6,10] ,价值和为 31 。
- 第二条路径节点为 [2] ,价值为 [7] 。
最大路径和与最小路径和的差值为 24 。24 是所有方案中的最大开销。
示例 2:
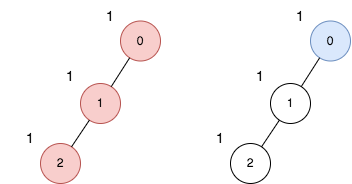
输入:n = 3, edges = [[0,1],[1,2]], price = [1,1,1]
输出:2
解释:上图展示了以节点 0 为根的树。左图(红色的节点)是最大价值和路径,右图(蓝色的节点)是最小价值和路径。
- 第一条路径包含节点 [0,1,2]:价值为 [1,1,1] ,价值和为 3 。
- 第二条路径节点为 [0] ,价值为 [1] 。
最大路径和与最小路径和的差值为 2 。2 是所有方案中的最大开销。
提示:
1 <= n <= 105edges.length == n - 10 <= ai, bi <= n - 1edges表示一棵符合题面要求的树。price.length == n1 <= price[i] <= 105
Metadata
- Link: Difference Between Maximum and Minimum Price Sum
- Difficulty: Hard
- Tag:
There exists an undirected and initially unrooted tree with n nodes indexed from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.
Each node has an associated price. You are given an integer array price, where price[i] is the price of the ith node.
The price sum of a given path is the sum of the prices of all nodes lying on that path.
The tree can be rooted at any node root of your choice. The incurred cost after choosing root is the difference between the maximum and minimum price sum amongst all paths starting at root.
Return the maximum possible cost amongst all possible root choices.
Example 1:

Input: n = 6, edges = [[0,1],[1,2],[1,3],[3,4],[3,5]], price = [9,8,7,6,10,5]
Output: 24
Explanation: The diagram above denotes the tree after rooting it at node 2. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes [2,1,3,4]: the prices are [7,8,6,10], and the sum of the prices is 31.
- The second path contains the node [2] with the price [7].
The difference between the maximum and minimum price sum is 24. It can be proved that 24 is the maximum cost.
Example 2:

Input: n = 3, edges = [[0,1],[1,2]], price = [1,1,1]
Output: 2
Explanation: The diagram above denotes the tree after rooting it at node 0. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes [0,1,2]: the prices are [1,1,1], and the sum of the prices is 3.
- The second path contains node [0] with a price [1].
The difference between the maximum and minimum price sum is 2. It can be proved that 2 is the maximum cost.
Constraints:
1 <= n <= 105edges.length == n - 10 <= ai, bi <= n - 1edgesrepresents a valid tree.price.length == n1 <= price[i] <= 105
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
struct Node {
ll mx{0};
ll mx_without_endpoint{0};
};
class Solution {
public:
vector<int> price;
vector<Node> node_vec;
vector<vector<int>> G;
ll res;
void dfs(int u, int fa) {
auto tmp = vector<Node>();
for (const auto &v : G[u]) {
if (v == fa) {
continue;
}
dfs(v, u);
tmp.push_back(node_vec[v]);
}
int p = price[u];
auto &u_node = node_vec[u];
ll mx_mx = 0;
ll mx_mx_without_endpoint = -0x3f3f3f3f3f3f3f3f;
u_node.mx = p;
for (const auto &node : tmp) {
res = max(res, mx_mx);
res = max(res, mx_mx_without_endpoint + p);
res = max(res, mx_mx + node.mx_without_endpoint + p);
res = max(res, mx_mx_without_endpoint + node.mx + p);
mx_mx = max(mx_mx, node.mx);
mx_mx_without_endpoint = max(mx_mx_without_endpoint, node.mx_without_endpoint);
u_node.mx = max(u_node.mx, node.mx + p);
u_node.mx_without_endpoint = max(u_node.mx_without_endpoint, node.mx_without_endpoint + p);
}
res = max(res, mx_mx);
res = max(res, mx_mx_without_endpoint + p);
}
long long maxOutput(int n, vector<vector<int>> &edges, vector<int> &price) {
G = vector<vector<int>>(n + 1, vector<int>());
this->price = price;
node_vec = vector<Node>(n + 1, Node{});
res = 0;
for (const auto &e : edges) {
int u = e[0];
int v = e[1];
G[u].push_back(v);
G[v].push_back(u);
}
dfs(0, -1);
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif