跳转至

weekly-contest-206

A

Statement

Metadata

给你一个大小为 rows x cols 的矩阵 mat，其中 mat[i][j] 是 0 或 1，请返回 矩阵 mat 中特殊位置的数目 。

特殊位置 定义：如果 mat[i][j] == 1 并且第 i 行和第 j 列中的所有其他元素均为 0（行和列的下标均 从 0 开始 ），则位置 (i, j) 被称为特殊位置。

 

示例 1：

输入：mat = [[1,0,0],
            [0,0,1],
            [1,0,0]]
输出：1
解释：(1,2) 是一个特殊位置，因为 mat[1][2] == 1 且所处的行和列上所有其他元素都是 0

示例 2：

输入：mat = [[1,0,0],
            [0,1,0],
            [0,0,1]]
输出：3
解释：(0,0), (1,1) 和 (2,2) 都是特殊位置

示例 3：

输入：mat = [[0,0,0,1],
            [1,0,0,0],
            [0,1,1,0],
            [0,0,0,0]]
输出：2

示例 4：

输入：mat = [[0,0,0,0,0],
            [1,0,0,0,0],
            [0,1,0,0,0],
            [0,0,1,0,0],
            [0,0,0,1,1]]
输出：3

 

提示：

  • rows == mat.length
  • cols == mat[i].length
  • 1 <= rows, cols <= 100
  • mat[i][j] 是 0 或 1

Metadata

Given an m x n binary matrix mat, return the number of special positions in mat.

A position (i, j) is called special if mat[i][j] == 1 and all other elements in row i and column j are 0 (rows and columns are 0-indexed).

 

Example 1:

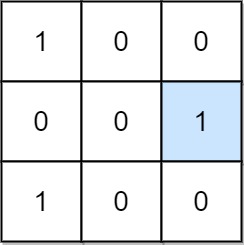
Input: mat = [[1,0,0],[0,0,1],[1,0,0]]
Output: 1
Explanation: (1, 2) is a special position because mat[1][2] == 1 and all other elements in row 1 and column 2 are 0.

Example 2:

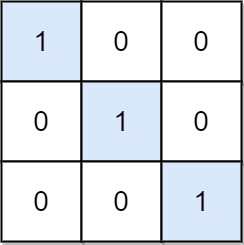
Input: mat = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3
Explanation: (0, 0), (1, 1) and (2, 2) are special positions.

 

Constraints:

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 100
  • mat[i][j] is either 0 or 1.

Solution

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
int n;

class Solution {
public:
    int numSpecial(vector<vector<int>> &mat) {
        int n = SZ(mat);
        int m = SZ(mat[0]);
        int res = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                if (mat[i][j] == 1) {
                    int ok = 1;
                    for (int k = 0; k < m; ++k) {
                        if (k != j && mat[i][k] == 1)
                            ok = 0;
                    }
                    for (int k = 0; k < n; ++k) {
                        if (k != i && mat[k][j] == 1)
                            ok = 0;
                    }
                    res += ok;
                }
            }
        }
        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

B

Statement

Metadata

给你一份 n 位朋友的亲近程度列表，其中 n 总是 偶数 。

对每位朋友 i，preferences[i] 包含一份 按亲近程度从高到低排列 的朋友列表。换句话说，排在列表前面的朋友与 i 的亲近程度比排在列表后面的朋友更高。每个列表中的朋友均以 0 到 n-1 之间的整数表示。

所有的朋友被分成几对，配对情况以列表 pairs 给出，其中 pairs[i] = [xi, yi] 表示 xi 与 yi 配对，且 yi 与 xi 配对。

但是，这样的配对情况可能会使其中部分朋友感到不开心。在 x 与 y 配对且 u 与 v 配对的情况下，如果同时满足下述两个条件，x 就会不开心：

  • x 与 u 的亲近程度胜过 x 与 y，且
  • u 与 x 的亲近程度胜过 u 与 v

返回 不开心的朋友的数目 。

 

示例 1：

输入：n = 4, preferences = [[1, 2, 3], [3, 2, 0], [3, 1, 0], [1, 2, 0]], pairs = [[0, 1], [2, 3]]
输出：2
解释：
朋友 1 不开心，因为：
- 1 与 0 配对，但 1 与 3 的亲近程度比 1 与 0 高，且
- 3 与 1 的亲近程度比 3 与 2 高。
朋友 3 不开心，因为：
- 3 与 2 配对，但 3 与 1 的亲近程度比 3 与 2 高，且
- 1 与 3 的亲近程度比 1 与 0 高。
朋友 0 和 2 都是开心的。

示例 2：

输入：n = 2, preferences = [[1], [0]], pairs = [[1, 0]]
输出：0
解释：朋友 0 和 1 都开心。

示例 3：

输入：n = 4, preferences = [[1, 3, 2], [2, 3, 0], [1, 3, 0], [0, 2, 1]], pairs = [[1, 3], [0, 2]]
输出：4

 

提示：

  • 2 <= n <= 500
  • n 是偶数
  • preferences.length == n
  • preferences[i].length == n - 1
  • 0 <= preferences[i][j] <= n - 1
  • preferences[i] 不包含 i
  • preferences[i] 中的所有值都是独一无二的
  • pairs.length == n/2
  • pairs[i].length == 2
  • xi != yi
  • 0 <= xi, yi <= n - 1
  • 每位朋友都 恰好 被包含在一对中

Metadata

You are given a list of preferences for n friends, where n is always even.

For each person i, preferences[i] contains a list of friends sorted in the order of preference. In other words, a friend earlier in the list is more preferred than a friend later in the list. Friends in each list are denoted by integers from 0 to n-1.

All the friends are divided into pairs. The pairings are given in a list pairs, where pairs[i] = [xi, yi] denotes xi is paired with yi and yi is paired with xi.

However, this pairing may cause some of the friends to be unhappy. A friend x is unhappy if x is paired with y and there exists a friend u who is paired with v but:

  • x prefers u over y, and
  • u prefers x over v.

Return the number of unhappy friends.

 

Example 1:

Input: n = 4, preferences = [[1, 2, 3], [3, 2, 0], [3, 1, 0], [1, 2, 0]], pairs = [[0, 1], [2, 3]]
Output: 2
Explanation:
Friend 1 is unhappy because:
- 1 is paired with 0 but prefers 3 over 0, and
- 3 prefers 1 over 2.
Friend 3 is unhappy because:
- 3 is paired with 2 but prefers 1 over 2, and
- 1 prefers 3 over 0.
Friends 0 and 2 are happy.

Example 2:

Input: n = 2, preferences = [[1], [0]], pairs = [[1, 0]]
Output: 0
Explanation: Both friends 0 and 1 are happy.

Example 3:

Input: n = 4, preferences = [[1, 3, 2], [2, 3, 0], [1, 3, 0], [0, 2, 1]], pairs = [[1, 3], [0, 2]]
Output: 4

 

Constraints:

  • 2 <= n <= 500
  • n is even.
  • preferences.length == n
  • preferences[i].length == n - 1
  • 0 <= preferences[i][j] <= n - 1
  • preferences[i] does not contain i.
  • All values in preferences[i] are unique.
  • pairs.length == n/2
  • pairs[i].length == 2
  • xi != yi
  • 0 <= xi, yi <= n - 1
  • Each person is contained in exactly one pair.

Solution

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1& x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1& x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1& x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T& arg, Ts&... args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T& arg, const Ts&... args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t>& arg, const A&... args) {
    for (auto& v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T& arg, const Ts&... args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T& arg, const Ts&... args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t>& arg, const A&... args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 5e2 + 10;
int n;
int vis[N], g[N][N];

inline void ok(int x, int y, int u, int v) {
    if (g[x][u] < g[x][y] && g[u][x] < g[u][v])
        vis[x] = 1;
}

class Solution {
public:
    int unhappyFriends(int n, vector<vector<int>>& preferences, vector<vector<int>>& pairs) {
        int res = 0;
        for (int i = 0; i <= n; ++i) vis[i] = 0;
        int m = n / 2;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n - 1; ++j) {
                g[i][preferences[i][j]] = j;
            }
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < m; ++j)
                if (i != j) {
                    int x = pairs[i][0], y = pairs[i][1];
                    int u = pairs[j][0], v = pairs[j][1];
                    ok(x, y, u, v);
                    ok(x, y, v, u);
                    ok(y, x, u, v);
                    ok(y, x, v, u);
                }
        }
        for (int i = 0; i < n; ++i) res += vis[i];
        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

C

Statement

Metadata

给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。

连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 ：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。

请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。

 

示例 1：

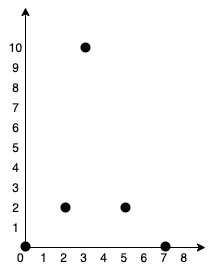
输入：points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出：20
解释：

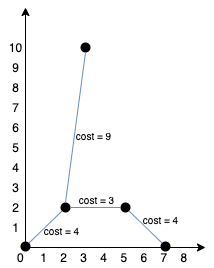我们可以按照上图所示连接所有点得到最小总费用，总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达。

示例 2：

输入：points = [[3,12],[-2,5],[-4,1]]
输出：18

示例 3：

输入：points = [[0,0],[1,1],[1,0],[-1,1]]
输出：4

示例 4：

输入：points = [[-1000000,-1000000],[1000000,1000000]]
输出：4000000

示例 5：

输入：points = [[0,0]]
输出：0

 

提示：

  • 1 <= points.length <= 1000
  • -106 <= xi, yi <= 106
  • 所有点 (xi, yi) 两两不同。

Metadata

You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].

The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.

Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.

 

Example 1:

Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output: 20
Explanation: 

We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.

Example 2:

Input: points = [[3,12],[-2,5],[-4,1]]
Output: 18

 

Constraints:

  • 1 <= points.length <= 1000
  • -106 <= xi, yi <= 106
  • All pairs (xi, yi) are distinct.

Solution

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e3 + 10;
constexpr int INF = 0x3f3f3f3f;
int n, m;
int g[N][N];
vector<vector<int>> points;
int vis[N];
int lowc[N];

int Prim() {
    int ans = 0;
    memset(vis, 0, sizeof vis);
    vis[0] = 1;
    for (int i = 1; i < n; ++i) lowc[i] = g[0][i];
    for (int i = 1; i < n; ++i) {
        int minc = INF;
        int p = -1;
        for (int j = 0; j < n; ++j) {
            if (!vis[j] && minc > lowc[j]) {
                minc = lowc[j];
                p = j;
            }
        }
        if (minc == INF)
            return -1;
        ans += minc;
        vis[p] = 1;
        for (int j = 0; j < n; ++j) {
            if (!vis[j] && lowc[j] > g[p][j]) {
                lowc[j] = g[p][j];
            }
        }
    }
    return ans;
}

inline int dis(int a, int b) {
    return abs(points[a][0] - points[b][0]) + abs(points[a][1] - points[b][1]);
}

class Solution {
public:
    int minCostConnectPoints(vector<vector<int>> &_points) {
        points = _points;
        n = SZ(points);
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                g[i][j] = dis(i, j);
            }
        }
        return Prim();
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif

D

Statement

Metadata

给你两个字符串 s 和 t ，请你通过若干次以下操作将字符串 s 转化成字符串 t ：

  • 选择 s 中一个 非空 子字符串并将它包含的字符就地 升序 排序。

比方说，对下划线所示的子字符串进行操作可以由 "14234" 得到 "12344" 。

如果可以将字符串 s 变成 t ，返回 true 。否则，返回 false 。

一个 子字符串 定义为一个字符串中连续的若干字符。

 

示例 1：

输入：s = "84532", t = "34852"
输出：true
解释：你可以按以下操作将 s 转变为 t ：
"84532" （从下标 2 到下标 3）-> "84352"
"84352" （从下标 0 到下标 2） -> "34852"

示例 2：

输入：s = "34521", t = "23415"
输出：true
解释：你可以按以下操作将 s 转变为 t ：
"34521" -> "23451"
"23451" -> "23415"

示例 3：

输入：s = "12345", t = "12435"
输出：false

示例 4：

输入：s = "1", t = "2"
输出：false

 

提示：

  • s.length == t.length
  • 1 <= s.length <= 105
  • s 和 t 都只包含数字字符，即 '0' 到 '9' 。

Metadata

Given two strings s and t, transform string s into string t using the following operation any number of times:

  • Choose a non-empty substring in s and sort it in place so the characters are in ascending order.
    • For example, applying the operation on the underlined substring in "14234" results in "12344".

Return true if it is possible to transform s into t. Otherwise, return false.

A substring is a contiguous sequence of characters within a string.

 

Example 1:

Input: s = "84532", t = "34852"
Output: true
Explanation: You can transform s into t using the following sort operations:
"84532" (from index 2 to 3) -> "84352"
"84352" (from index 0 to 2) -> "34852"

Example 2:

Input: s = "34521", t = "23415"
Output: true
Explanation: You can transform s into t using the following sort operations:
"34521" -> "23451"
"23451" -> "23415"

Example 3:

Input: s = "12345", t = "12435"
Output: false

 

Constraints:

  • s.length == t.length
  • 1 <= s.length <= 105
  • s and t consist of only digits.

Solution

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define mkp make_pair
#define all(x) (x).begin(), (x).end()
using db = double;
using ll = long long;
using ull = unsigned long long;
using pII = pair<int, int>;
using pLL = pair<ll, ll>;
constexpr int mod = 1e9 + 7;
template <class T1, class T2>
inline void chadd(T1 &x, T2 y, int Mod = mod) {
    x += y;
    while (x >= Mod) x -= Mod;
    while (x < 0) x += Mod;
}
template <class T1, class T2>
inline void chmax(T1 &x, T2 y) {
    if (x < y)
        x = y;
}
template <class T1, class T2>
inline void chmin(T1 &x, T2 y) {
    if (x > y)
        x = y;
}
inline int nextInt() {
    int x;
    cin >> x;
    return x;
}
void rd() {}
template <class T, class... Ts>
void rd(T &arg, Ts &...args) {
    cin >> arg;
    rd(args...);
}
#define dbg(x...)                             \
    do {                                      \
        cout << "\033[32;1m" << #x << " -> "; \
        err(x);                               \
    } while (0)
void err() {
    cout << "\033[39;0m" << endl;
}
template <class T, class... Ts>
void err(const T &arg, const Ts &...args) {
    cout << arg << ' ';
    err(args...);
}
template <template <typename...> class T, typename t, typename... A>
void err(const T<t> &arg, const A &...args) {
    for (auto &v : arg) cout << v << ' ';
    err(args...);
}
void ptt() {
    cout << endl;
}
template <class T, class... Ts>
void ptt(const T &arg, const Ts &...args) {
    cout << ' ' << arg;
    ptt(args...);
}
template <class T, class... Ts>
void pt(const T &arg, const Ts &...args) {
    cout << arg;
    ptt(args...);
}
void pt() {}
template <template <typename...> class T, typename t, typename... A>
void pt(const T<t> &arg, const A &...args) {
    for (int i = 0, sze = arg.size(); i < sze; ++i) cout << arg[i] << " \n"[i == sze - 1];
    pt(args...);
}
inline ll qpow(ll base, ll n) {
    assert(n >= 0);
    ll res = 1;
    while (n) {
        if (n & 1)
            res = res * base % mod;
        base = base * base % mod;
        n >>= 1;
    }
    return res;
}
// head
constexpr int N = 1e5 + 10;
int n;

class Solution {
public:
    bool isTransformable(string s, string t) {
        vector<int> vec[15];
        n = SZ(s);
        for (int i = 0; i < n; ++i) {
            int num = s[i] - '0';
            vec[num].push_back(i);
        }
        reverse(all(t));
        for (auto &ch : t) {
            int num = ch - '0';
            if (!vec[num].empty()) {
                int ok = 1;
                for (int i = num + 1; i < 10; ++i) {
                    if (!vec[i].empty() && vec[i].back() > vec[num].back()) {
                        ok = 0;
                        break;
                    }
                }
                if (ok) {
                    vec[num].pop_back();
                } else {
                    return false;
                }
            } else {
                return false;
            }
        }
        return true;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif
最后更新: October 11, 2023
回到页面顶部