weekly-contest-319
A
Statement
Metadata
- Link: 温度转换
- Difficulty: Easy
- Tag:
给你一个四舍五入到两位小数的非负浮点数 celsius 来表示温度,以 摄氏度(Celsius)为单位。
你需要将摄氏度转换为 开氏度(Kelvin)和 华氏度(Fahrenheit),并以数组 ans = [kelvin, fahrenheit] 的形式返回结果。
返回数组 ans 。与实际答案误差不超过 10-5 的会视为正确答案。
注意:
开氏度 = 摄氏度 + 273.15华氏度 = 摄氏度 * 1.80 + 32.00
示例 1 :
输入:celsius = 36.50
输出:[309.65000,97.70000]
解释:36.50 摄氏度:转换为开氏度是 309.65 ,转换为华氏度是 97.70 。示例 2 :
输入:celsius = 122.11
输出:[395.26000,251.79800]
解释:122.11 摄氏度:转换为开氏度是 395.26 ,转换为华氏度是 251.798 。
提示:
0 <= celsius <= 1000
Metadata
- Link: Convert the Temperature
- Difficulty: Easy
- Tag:
You are given a non-negative floating point number rounded to two decimal places celsius, that denotes the temperature in Celsius.
You should convert Celsius into Kelvin and Fahrenheit and return it as an array ans = [kelvin, fahrenheit].
Return the array ans. Answers within 10-5 of the actual answer will be accepted.
Note that:
Kelvin = Celsius + 273.15Fahrenheit = Celsius * 1.80 + 32.00
Example 1:
Input: celsius = 36.50
Output: [309.65000,97.70000]
Explanation: Temperature at 36.50 Celsius converted in Kelvin is 309.65 and converted in Fahrenheit is 97.70.
Example 2:
Input: celsius = 122.11
Output: [395.26000,251.79800]
Explanation: Temperature at 122.11 Celsius converted in Kelvin is 395.26 and converted in Fahrenheit is 251.798.
Constraints:
0 <= celsius <= 1000
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
vector<double> convertTemperature(double celsius) {
return vector<double>({celsius + 273.15, celsius * 1.8 + 32});
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 最小公倍数为 K 的子数组数目
- Difficulty: Medium
- Tag:
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 nums 的 子数组 中满足 元素最小公倍数为 k 的子数组数目。
子数组 是数组中一个连续非空的元素序列。
数组的最小公倍数 是可被所有数组元素整除的最小正整数。
示例 1 :
输入:nums = [3,6,2,7,1], k = 6
输出:4
解释:以 6 为最小公倍数的子数组是:
- [3,6,2,7,1]
- [3,6,2,7,1]
- [3,6,2,7,1]
- [3,6,2,7,1]
示例 2 :
输入:nums = [3], k = 2
输出:0
解释:不存在以 2 为最小公倍数的子数组。
提示:
1 <= nums.length <= 10001 <= nums[i], k <= 1000
Metadata
- Link: Number of Subarrays With LCM Equal to K
- Difficulty: Medium
- Tag:
Given an integer array nums and an integer k, return the number of subarrays of nums where the least common multiple of the subarray's elements is k.
A subarray is a contiguous non-empty sequence of elements within an array.
The least common multiple of an array is the smallest positive integer that is divisible by all the array elements.
Example 1:
Input: nums = [3,6,2,7,1], k = 6
Output: 4
Explanation: The subarrays of nums where 6 is the least common multiple of all the subarray's elements are:
- [3,6,2,7,1]
- [3,6,2,7,1]
- [3,6,2,7,1]
- [3,6,2,7,1]
Example 2:
Input: nums = [3], k = 2
Output: 0
Explanation: There are no subarrays of nums where 2 is the least common multiple of all the subarray's elements.
Constraints:
1 <= nums.length <= 10001 <= nums[i], k <= 1000
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int subarrayLCM(vector<int> &nums, int k) {
int n = int(nums.size());
int res = 0;
for (int i = 0; i < n; i++) {
ll pre = 1;
for (int j = i; j < n; j++) {
pre = pre * nums[j] / __gcd(pre, ll(nums[j]));
if (pre > k) {
break;
}
if (pre == k) {
++res;
}
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 逐层排序二叉树所需的最少操作数目
- Difficulty: Medium
- Tag:
给你一个 值互不相同 的二叉树的根节点 root 。
在一步操作中,你可以选择 同一层 上任意两个节点,交换这两个节点的值。
返回每一层按 严格递增顺序 排序所需的最少操作数目。
节点的 层数 是该节点和根节点之间的路径的边数。
示例 1 :
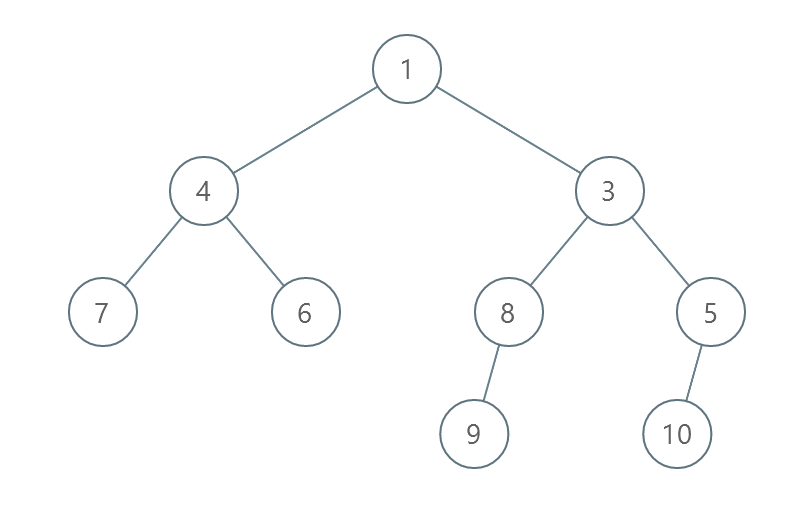
输入:root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
输出:3
解释:
- 交换 4 和 3 。第 2 层变为 [3,4] 。
- 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
- 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。
共计用了 3 步操作,所以返回 3 。
可以证明 3 是需要的最少操作数目。
示例 2 :
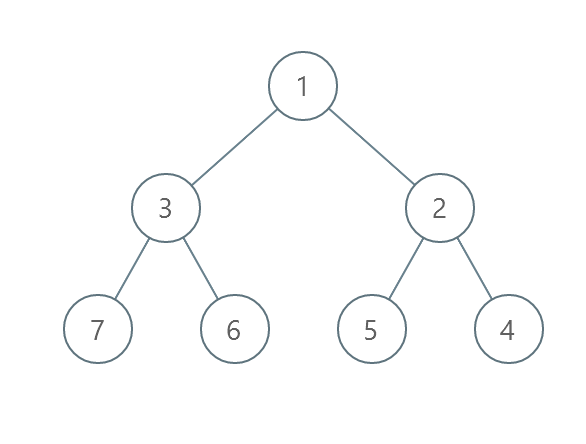
输入:root = [1,3,2,7,6,5,4]
输出:3
解释:
- 交换 3 和 2 。第 2 层变为 [2,3] 。
- 交换 7 和 4 。第 3 层变为 [4,6,5,7] 。
- 交换 6 和 5 。第 3 层变为 [4,5,6,7] 。
共计用了 3 步操作,所以返回 3 。
可以证明 3 是需要的最少操作数目。
示例 3 :
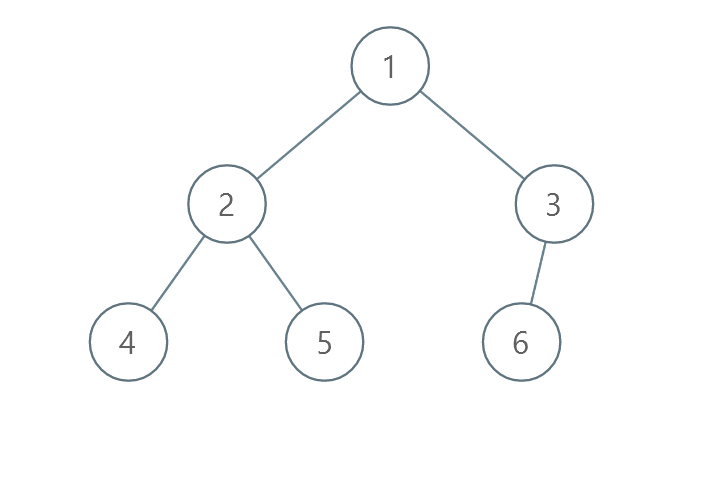
输入:root = [1,2,3,4,5,6]
输出:0
解释:每一层已经按递增顺序排序,所以返回 0 。
提示:
- 树中节点的数目在范围
[1, 105]。 1 <= Node.val <= 105- 树中的所有值 互不相同 。
Metadata
- Link: Minimum Number of Operations to Sort a Binary Tree by Level
- Difficulty: Medium
- Tag:
You are given the root of a binary tree with unique values.
In one operation, you can choose any two nodes at the same level and swap their values.
Return the minimum number of operations needed to make the values at each level sorted in a strictly increasing order.
The level of a node is the number of edges along the path between it and the root node.
Example 1:

Input: root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
Output: 3
Explanation:
- Swap 4 and 3. The 2nd level becomes [3,4].
- Swap 7 and 5. The 3rd level becomes [5,6,8,7].
- Swap 8 and 7. The 3rd level becomes [5,6,7,8].
We used 3 operations so return 3.
It can be proven that 3 is the minimum number of operations needed.
Example 2:

Input: root = [1,3,2,7,6,5,4]
Output: 3
Explanation:
- Swap 3 and 2. The 2nd level becomes [2,3].
- Swap 7 and 4. The 3rd level becomes [4,6,5,7].
- Swap 6 and 5. The 3rd level becomes [4,5,6,7].
We used 3 operations so return 3.
It can be proven that 3 is the minimum number of operations needed.
Example 3:

Input: root = [1,2,3,4,5,6]
Output: 0
Explanation: Each level is already sorted in increasing order so return 0.
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 105- All the values of the tree are unique.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
#ifdef LOCAL
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
#endif
class Solution {
public:
vector<vector<int>> vec;
int max_depth = 0;
void getMaxDepth(TreeNode *rt, int deep) {
if (!rt) {
return;
}
max_depth = max(max_depth, deep);
getMaxDepth(rt->left, deep + 1);
getMaxDepth(rt->right, deep + 1);
}
void dfs(TreeNode *rt, int deep) {
if (!rt) {
return;
}
vec[deep].push_back(rt->val);
dfs(rt->left, deep + 1);
dfs(rt->right, deep + 1);
}
int getMinSwaps(const vector<int> &A) {
vector<int> B(A);
sort(B.begin(), B.end());
map<int, int> m;
int len = (int)A.size();
for (int i = 0; i < len; i++) {
m[B[i]] = i;
}
int loops = 0;
vector<bool> flag(len, false);
for (int i = 0; i < len; i++) {
if (!flag[i]) {
int j = i;
while (!flag[j]) {
flag[j] = true;
j = m[A[j]];
}
loops++;
}
}
return len - loops;
}
int minimumOperations(TreeNode *root) {
max_depth = 0;
getMaxDepth(root, 1);
vec = vector<vector<int>>(max_depth + 5, vector<int>());
dfs(root, 0);
int res = 0;
for (const auto &v : vec) {
res += getMinSwaps(v);
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 不重叠回文子字符串的最大数目
- Difficulty: Hard
- Tag:
给你一个字符串 s 和一个 正 整数 k 。
从字符串 s 中选出一组满足下述条件且 不重叠 的子字符串:
- 每个子字符串的长度 至少 为
k。 - 每个子字符串是一个 回文串 。
返回最优方案中能选择的子字符串的 最大 数目。
子字符串 是字符串中一个连续的字符序列。
示例 1 :
输入:s = "abaccdbbd", k = 3
输出:2
解释:可以选择 s = "abaccdbbd" 中斜体加粗的子字符串。"aba" 和 "dbbd" 都是回文,且长度至少为 k = 3 。
可以证明,无法选出两个以上的有效子字符串。
示例 2 :
输入:s = "adbcda", k = 2
输出:0
解释:字符串中不存在长度至少为 2 的回文子字符串。
提示:
1 <= k <= s.length <= 2000s仅由小写英文字母组成
Metadata
- Link: Maximum Number of Non-overlapping Palindrome Substrings
- Difficulty: Hard
- Tag:
You are given a string s and a positive integer k.
Select a set of non-overlapping substrings from the string s that satisfy the following conditions:
- The length of each substring is at least
k. - Each substring is a palindrome.
Return the maximum number of substrings in an optimal selection.
A substring is a contiguous sequence of characters within a string.
Example 1:
Input: s = "abaccdbbd", k = 3
Output: 2
Explanation: We can select the substrings underlined in s = "abaccdbbd". Both "aba" and "dbbd" are palindromes and have a length of at least k = 3.
It can be shown that we cannot find a selection with more than two valid substrings.
Example 2:
Input: s = "adbcda", k = 2
Output: 0
Explanation: There is no palindrome substring of length at least 2 in the string.
Constraints:
1 <= k <= s.length <= 2000sconsists of lowercase English letters.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Manacher {
public:
Manacher() {}
Manacher(const int n) {
fake_s_.reserve(n << 1);
u.reserve(n << 1);
}
~Manacher() {}
// 0-index
void Build(const char *s, size_t len) {
this->len = static_cast<int>(len);
fake_s_.resize((len + 1) << 2);
u.resize((len + 1) << 2);
l = 0;
fake_s_[l++] = '$';
fake_s_[l++] = '#';
for (size_t i = 0; i < len; i++) {
fake_s_[l++] = s[i];
fake_s_[l++] = '#';
}
fake_s_[l] = 0;
int mx = 0, id = 0;
for (int i = 0; i < l; i++) {
u[i] = mx > i ? std::min(u[2 * id - i], mx - i) : 1;
while (i - u[i] >= 0 && fake_s_[i + u[i]] == fake_s_[i - u[i]]) {
u[i]++;
}
if (i + u[i] > mx) {
mx = i + u[i];
id = i;
}
}
fake_s_.resize(l);
u.resize(l);
}
void Build(const char *s) {
Build(s, strlen(s));
}
void Build(const std::string &s) {
Build(s.c_str(), s.length());
}
// check if s[l:r + 1] is a palindrome.
bool IsPalindrome(int l, int r) const {
int il = (l + 1) * 2, ir = (r + 1) * 2;
int mid = (il + ir) / 2;
int len = (r - l + 2) / 2;
return (u[mid] / 2) >= len;
}
// get the length of the longest palindrome substring
int GetMaxLengthOfPalindromeSubstring() const {
int res = 0;
for (int i = 0; i < l; i++) {
res = std::max(res, u[i] - 1);
}
return res;
}
const std::vector<int> &GetU() {
return u;
}
private:
int len, l;
std::vector<char> fake_s_;
std::vector<int> u;
};
class Solution {
public:
int maxPalindromes(string s, int k) {
int n = int(s.size());
auto m = Manacher(n + 5);
m.Build(s);
auto f = vector<int>(n + 5, 0);
for (int i = 1; i <= n; i++) {
for (int j = i - k + 1; j >= 1; j--) {
if (m.IsPalindrome(j - 1, i - 1)) {
f[i] = max(f[i], f[j - 1] + 1);
}
}
f[i] = max(f[i], f[i - 1]);
}
return f[n];
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif