weekly-contest-299
A
Statement
Metadata
- Link: 判断矩阵是否是一个 X 矩阵
- Difficulty: Easy
- Tag:
如果一个正方形矩阵满足下述 全部 条件,则称之为一个 X 矩阵 :
- 矩阵对角线上的所有元素都 不是 0
- 矩阵中所有其他元素都是 0
给你一个大小为 n x n 的二维整数数组 grid ,表示一个正方形矩阵。如果 grid 是一个 X 矩阵 ,返回 true ;否则,返回 false 。
示例 1:

输入:grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]]
输出:true
解释:矩阵如上图所示。
X 矩阵应该满足:绿色元素(对角线上)都不是 0 ,红色元素都是 0 。
因此,grid 是一个 X 矩阵。
示例 2:

输入:grid = [[5,7,0],[0,3,1],[0,5,0]]
输出:false
解释:矩阵如上图所示。
X 矩阵应该满足:绿色元素(对角线上)都不是 0 ,红色元素都是 0 。
因此,grid 不是一个 X 矩阵。
提示:
n == grid.length == grid[i].length3 <= n <= 1000 <= grid[i][j] <= 105
Metadata
- Link: Check if Matrix Is X-Matrix
- Difficulty: Easy
- Tag:
A square matrix is said to be an X-Matrix if both of the following conditions hold:
- All the elements in the diagonals of the matrix are non-zero.
- All other elements are 0.
Given a 2D integer array grid of size n x n representing a square matrix, return true if grid is an X-Matrix. Otherwise, return false.
Example 1:

Input: grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]]
Output: true
Explanation: Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is an X-Matrix.
Example 2:

Input: grid = [[5,7,0],[0,3,1],[0,5,0]]
Output: false
Explanation: Refer to the diagram above.
An X-Matrix should have the green elements (diagonals) be non-zero and the red elements be 0.
Thus, grid is not an X-Matrix.
Constraints:
n == grid.length == grid[i].length3 <= n <= 1000 <= grid[i][j] <= 105
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
bool checkXMatrix(vector<vector<int>> &grid) {
int n = grid.size();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j) {
if (grid[i][j] == 0)
return false;
} else if (i + j == n - 1) {
if (grid[i][j] == 0)
return false;
} else if (grid[i][j] != 0) {
return false;
}
}
}
return true;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 统计放置房子的方式数
- Difficulty: Medium
- Tag:
一条街道上共有 n * 2 个 地块 ,街道的两侧各有 n 个地块。每一边的地块都按从 1 到 n 编号。每个地块上都可以放置一所房子。
现要求街道同一侧不能存在两所房子相邻的情况,请你计算并返回放置房屋的方式数目。由于答案可能很大,需要对 109 + 7 取余后再返回。
注意,如果一所房子放置在这条街某一侧上的第 i 个地块,不影响在另一侧的第 i 个地块放置房子。
示例 1:
输入:n = 1
输出:4
解释:
可能的放置方式:
1. 所有地块都不放置房子。
2. 一所房子放在街道的某一侧。
3. 一所房子放在街道的另一侧。
4. 放置两所房子,街道两侧各放置一所。
示例 2:
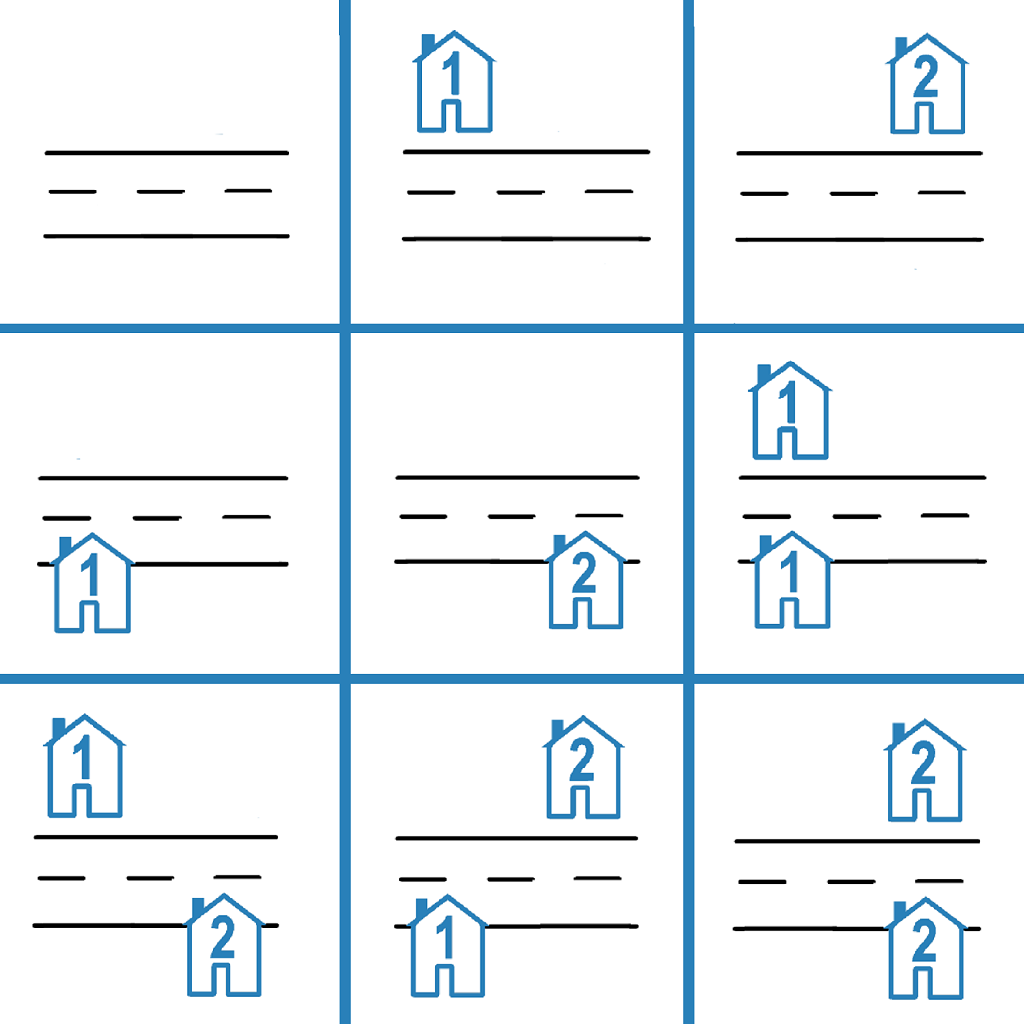
输入:n = 2
输出:9
解释:如上图所示,共有 9 种可能的放置方式。
提示:
1 <= n <= 104
Metadata
- Link: Count Number of Ways to Place Houses
- Difficulty: Medium
- Tag:
There is a street with n * 2 plots, where there are n plots on each side of the street. The plots on each side are numbered from 1 to n. On each plot, a house can be placed.
Return the number of ways houses can be placed such that no two houses are adjacent to each other on the same side of the street. Since the answer may be very large, return it modulo 109 + 7.
Note that if a house is placed on the ith plot on one side of the street, a house can also be placed on the ith plot on the other side of the street.
Example 1:
Input: n = 1
Output: 4
Explanation:
Possible arrangements:
1. All plots are empty.
2. A house is placed on one side of the street.
3. A house is placed on the other side of the street.
4. Two houses are placed, one on each side of the street.
Example 2:

Input: n = 2
Output: 9
Explanation: The 9 possible arrangements are shown in the diagram above.
Constraints:
1 <= n <= 104
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
const int mod = 1e9 + 7;
class Solution {
public:
int countHousePlacements(int n) {
static auto f = std::invoke([]() {
const int n = 1e4;
auto f = vector<vector<int>>(n + 5, vector<int>(2, 0));
f[0][0] = 1;
for (int i = 1; i <= n; i++) {
f[i][0] = f[i - 1][0] + f[i - 1][1];
f[i][0] %= mod;
f[i][1] = f[i - 1][0];
}
return f;
});
ll res = f[n][0] + f[n][1];
res %= mod;
res *= res;
res %= mod;
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 拼接数组的最大分数
- Difficulty: Hard
- Tag:
动态规划
给你两个下标从 0 开始的整数数组 nums1 和 nums2 ,长度都是 n 。
你可以选择两个整数 left 和 right ,其中 0 <= left <= right < n ,接着 交换 两个子数组 nums1[left…right] 和 nums2[left…right] 。
- 例如,设
nums1 = [1,2,3,4,5]和nums2 = [11,12,13,14,15],整数选择left = 1和right = 2,那么nums1会变为[1,12,13,4,5]而nums2会变为[11,2,3,14,15]。
你可以选择执行上述操作 一次 或不执行任何操作。
数组的 分数 取 sum(nums1) 和 sum(nums2) 中的最大值,其中 sum(arr) 是数组 arr 中所有元素之和。
返回 可能的最大分数 。
子数组 是数组中连续的一个元素序列。arr[left…right] 表示子数组包含 nums 中下标 left 和 right 之间的元素(含 下标 left 和 right 对应元素)。
示例 1:
输入:nums1 = [60,60,60], nums2 = [10,90,10]
输出:210
解释:选择 left = 1 和 right = 1 ,得到 nums1 = [60,90,60] 和 nums2 = [10,60,10] 。
分数为 max(sum(nums1), sum(nums2)) = max(210, 80) = 210 。示例 2:
输入:nums1 = [20,40,20,70,30], nums2 = [50,20,50,40,20]
输出:220
解释:选择 left = 3 和 right = 4 ,得到 nums1 = [20,40,20,40,20] 和 nums2 = [50,20,50,70,30] 。
分数为 max(sum(nums1), sum(nums2)) = max(140, 220) = 220 。
示例 3:
输入:nums1 = [7,11,13], nums2 = [1,1,1]
输出:31
解释:选择不交换任何子数组。
分数为 max(sum(nums1), sum(nums2)) = max(31, 3) = 31 。
提示:
n == nums1.length == nums2.length1 <= n <= 1051 <= nums1[i], nums2[i] <= 104
Metadata
- Link: Maximum Score Of Spliced Array
- Difficulty: Hard
- Tag:
Dynamic Programming
You are given two 0-indexed integer arrays nums1 and nums2, both of length n.
You can choose two integers left and right where 0 <= left <= right < n and swap the subarray nums1[left…right] with the subarray nums2[left…right].
- For example, if
nums1 = [1,2,3,4,5]andnums2 = [11,12,13,14,15]and you chooseleft = 1andright = 2,nums1becomes[1,12,13,4,5]andnums2becomes[11,2,3,14,15].
You may choose to apply the mentioned operation once or not do anything.
The score of the arrays is the maximum of sum(nums1) and sum(nums2), where sum(arr) is the sum of all the elements in the array arr.
Return the maximum possible score.
A subarray is a contiguous sequence of elements within an array. arr[left…right] denotes the subarray that contains the elements of nums between indices left and right (inclusive).
Example 1:
Input: nums1 = [60,60,60], nums2 = [10,90,10]
Output: 210
Explanation: Choosing left = 1 and right = 1, we have nums1 = [60,90,60] and nums2 = [10,60,10].
The score is max(sum(nums1), sum(nums2)) = max(210, 80) = 210.Example 2:
Input: nums1 = [20,40,20,70,30], nums2 = [50,20,50,40,20]
Output: 220
Explanation: Choosing left = 3, right = 4, we have nums1 = [20,40,20,40,20] and nums2 = [50,20,50,70,30].
The score is max(sum(nums1), sum(nums2)) = max(140, 220) = 220.
Example 3:
Input: nums1 = [7,11,13], nums2 = [1,1,1]
Output: 31
Explanation: We choose not to swap any subarray.
The score is max(sum(nums1), sum(nums2)) = max(31, 3) = 31.
Constraints:
n == nums1.length == nums2.length1 <= n <= 1051 <= nums1[i], nums2[i] <= 104
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <numeric>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int maximumsSplicedArray(vector<int> &nums1, vector<int> &nums2) {
auto f = [](vector<int> &nums1, vector<int> &nums2) {
int res = accumulate(nums1.begin(), nums1.end(), 0);
res = max(res, accumulate(nums2.begin(), nums2.end(), 0));
int n = int(nums1.size());
auto f = vector<int>(n + 5, 0);
for (int i = n; i >= 1; i--) {
f[i] = f[i + 1] + nums1[i - 1];
}
auto g = vector<vector<int>>(2, vector<int>(n + 5, 0));
for (int i = 1; i <= n; i++) {
g[0][i] = g[0][i - 1] + nums1[i - 1];
g[1][i] = g[1][i - 1] + nums2[i - 1];
}
int mx = 0;
for (int i = 1; i <= n; i++) {
mx = max(mx, g[0][i] - g[1][i]);
res = max(res, g[1][i] + f[i + 1] + mx);
}
return res;
};
int res = f(nums1, nums2);
res = max(res, f(nums2, nums1));
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 从树中删除边的最小分数
- Difficulty: Hard
- Tag:
存在一棵无向连通树,树中有编号从 0 到 n - 1 的 n 个节点, 以及 n - 1 条边。
给你一个下标从 0 开始的整数数组 nums ,长度为 n ,其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ,长度为 n - 1 ,其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边。
删除树中两条 不同 的边以形成三个连通组件。对于一种删除边方案,定义如下步骤以计算其分数:
- 分别获取三个组件 每个 组件中所有节点值的异或值。
- 最大 异或值和 最小 异或值的 差值 就是这一种删除边方案的分数。
- 例如,三个组件的节点值分别是:
[4,5,7]、[1,9]和[3,3,3]。三个异或值分别是4 ^ 5 ^ 7 = 6、1 ^ 9 = 8和3 ^ 3 ^ 3 = 3。最大异或值是8,最小异或值是3,分数是8 - 3 = 5。
返回在给定树上执行任意删除边方案可能的 最小 分数。
示例 1:
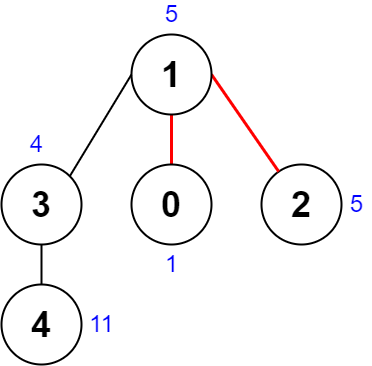
输入:nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
输出:9
解释:上图展示了一种删除边方案。
- 第 1 个组件的节点是 [1,3,4] ,值是 [5,4,11] 。异或值是 5 ^ 4 ^ 11 = 10 。
- 第 2 个组件的节点是 [0] ,值是 [1] 。异或值是 1 = 1 。
- 第 3 个组件的节点是 [2] ,值是 [5] 。异或值是 5 = 5 。
分数是最大异或值和最小异或值的差值,10 - 1 = 9 。
可以证明不存在分数比 9 小的删除边方案。
示例 2:
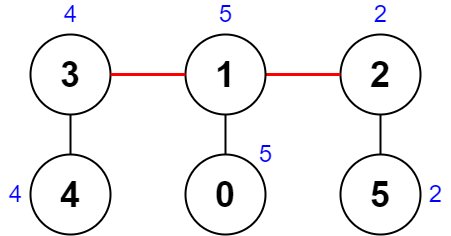
输入:nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]]
输出:0
解释:上图展示了一种删除边方案。
- 第 1 个组件的节点是 [3,4] ,值是 [4,4] 。异或值是 4 ^ 4 = 0 。
- 第 2 个组件的节点是 [1,0] ,值是 [5,5] 。异或值是 5 ^ 5 = 0 。
- 第 3 个组件的节点是 [2,5] ,值是 [2,2] 。异或值是 2 ^ 2 = 0 。
分数是最大异或值和最小异或值的差值,0 - 0 = 0 。
无法获得比 0 更小的分数 0 。
提示:
n == nums.length3 <= n <= 10001 <= nums[i] <= 108edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedges表示一棵有效的树
Metadata
- Link: Minimum Score After Removals on a Tree
- Difficulty: Hard
- Tag:
There is an undirected connected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.
You are given a 0-indexed integer array nums of length n where nums[i] represents the value of the ith node. You are also given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.
Remove two distinct edges of the tree to form three connected components. For a pair of removed edges, the following steps are defined:
- Get the XOR of all the values of the nodes for each of the three components respectively.
- The difference between the largest XOR value and the smallest XOR value is the score of the pair.
- For example, say the three components have the node values:
[4,5,7],[1,9], and[3,3,3]. The three XOR values are4 ^ 5 ^ 7 = 6,1 ^ 9 = 8, and3 ^ 3 ^ 3 = 3. The largest XOR value is8and the smallest XOR value is3. The score is then8 - 3 = 5.
Return the minimum score of any possible pair of edge removals on the given tree.
Example 1:

Input: nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
Output: 9
Explanation: The diagram above shows a way to make a pair of removals.
- The 1st component has nodes [1,3,4] with values [5,4,11]. Its XOR value is 5 ^ 4 ^ 11 = 10.
- The 2nd component has node [0] with value [1]. Its XOR value is 1 = 1.
- The 3rd component has node [2] with value [5]. Its XOR value is 5 = 5.
The score is the difference between the largest and smallest XOR value which is 10 - 1 = 9.
It can be shown that no other pair of removals will obtain a smaller score than 9.
Example 2:

Input: nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]]
Output: 0
Explanation: The diagram above shows a way to make a pair of removals.
- The 1st component has nodes [3,4] with values [4,4]. Its XOR value is 4 ^ 4 = 0.
- The 2nd component has nodes [1,0] with values [5,5]. Its XOR value is 5 ^ 5 = 0.
- The 3rd component has nodes [2,5] with values [2,2]. Its XOR value is 2 ^ 2 = 0.
The score is the difference between the largest and smallest XOR value which is 0 - 0 = 0.
We cannot obtain a smaller score than 0.
Constraints:
n == nums.length3 <= n <= 10001 <= nums[i] <= 108edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedgesrepresents a valid tree.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
vector<int> f, w;
vector<vector<int>> g, h;
void dfs(int u, int fa, vector<int> &fas) {
int xor_sum = w[u];
h[u] = vector<int>(fas);
fas[u] = 1;
for (auto &v : g[u]) {
if (v == fa) {
continue;
}
dfs(v, u, fas);
xor_sum ^= f[v];
}
f[u] = xor_sum;
fas[u] = 0;
}
int minimumScore(vector<int> &nums, vector<vector<int>> &edges) {
int n = int(nums.size());
w = vector<int>(nums);
f = vector<int>(n + 1, 0);
g = vector<vector<int>>(n + 1, vector<int>());
h = vector<vector<int>>(n + 1, vector<int>());
for (auto &e : edges) {
g[e[0]].push_back(e[1]);
g[e[1]].push_back(e[0]);
}
auto fas = vector<int>(n + 1, 0);
dfs(0, 0, fas);
int res = 2e9;
for (int i = 1; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int x = i;
int y = j;
if (h[y][x]) {
swap(x, y);
}
auto t = vector<int>();
t.reserve(3);
if (h[x][y] == 1) {
t.push_back(f[0] ^ f[y]);
t.push_back(f[x]);
t.push_back(f[y] ^ f[x]);
} else {
t.push_back(f[0] ^ f[x] ^ f[y]);
t.push_back(f[x]);
t.push_back(f[y]);
}
sort(t.begin(), t.end());
res = min(res, t[2] - t[0]);
}
}
return res;
}
};
#ifdef LOCAL
int main() {
{
auto nums = vector<int>({1, 5, 5, 4, 11});
auto edges = vector<vector<int>>({{0, 1}, {1, 2}, {1, 3}, {3, 4}});
auto s = Solution();
auto res = s.minimumScore(nums, edges);
cout << res << endl;
}
return 0;
}
#endif