biweekly-contest-89
A
Statement
Metadata
- Link: 有效时间的数目
- Difficulty: Easy
- Tag:
给你一个长度为 5 的字符串 time ,表示一个电子时钟当前的时间,格式为 "hh:mm" 。最早 可能的时间是 "00:00" ,最晚 可能的时间是 "23:59" 。
在字符串 time 中,被字符 ? 替换掉的数位是 未知的 ,被替换的数字可能是 0 到 9 中的任何一个。
请你返回一个整数 answer ,将每一个 ? 都用 0 到 9 中一个数字替换后,可以得到的有效时间的数目。
示例 1:
输入:time = "?5:00"
输出:2
解释:我们可以将 ? 替换成 0 或 1 ,得到 "05:00" 或者 "15:00" 。注意我们不能替换成 2 ,因为时间 "25:00" 是无效时间。所以我们有两个选择。
示例 2:
输入:time = "0?:0?"
输出:100
解释:两个 ? 都可以被 0 到 9 之间的任意数字替换,所以我们总共有 100 种选择。
示例 3:
输入:time = "??:??"
输出:1440
解释:小时总共有 24 种选择,分钟总共有 60 种选择。所以总共有 24 * 60 = 1440 种选择。
提示:
time是一个长度为5的有效字符串,格式为"hh:mm"。"00" <= hh <= "23""00" <= mm <= "59"- 字符串中有的数位是
'?',需要用0到9之间的数字替换。
Metadata
- Link: Number of Valid Clock Times
- Difficulty: Easy
- Tag:
You are given a string of length 5 called time, representing the current time on a digital clock in the format "hh:mm". The earliest possible time is "00:00" and the latest possible time is "23:59".
In the string time, the digits represented by the ? symbol are unknown, and must be replaced with a digit from 0 to 9.
Return an integer answer, the number of valid clock times that can be created by replacing every ? with a digit from 0 to 9.
Example 1:
Input: time = "?5:00"
Output: 2
Explanation: We can replace the ? with either a 0 or 1, producing "05:00" or "15:00". Note that we cannot replace it with a 2, since the time "25:00" is invalid. In total, we have two choices.
Example 2:
Input: time = "0?:0?"
Output: 100
Explanation: Each ? can be replaced by any digit from 0 to 9, so we have 100 total choices.
Example 3:
Input: time = "??:??"
Output: 1440
Explanation: There are 24 possible choices for the hours, and 60 possible choices for the minutes. In total, we have 24 * 60 = 1440 choices.
Constraints:
timeis a valid string of length5in the format"hh:mm"."00" <= hh <= "23""00" <= mm <= "59"- Some of the digits might be replaced with
'?'and need to be replaced with digits from0to9.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int ans = 0;
map<string, bool> mp;
int C(char c) {
return c - '0';
}
bool Done(const string &time) {
for (const auto &c : time) {
if (c == '?') {
return false;
}
}
return true;
}
bool OK(const string &time) {
int h = C(time[0]) * 10 + C(time[1]);
int m = C(time[3]) * 10 + C(time[4]);
if (h >= 0 && h <= 23 && m >= 0 && m <= 59) {
return true;
}
return false;
}
void DFS(string time) {
if (mp.count(time)) {
return;
}
mp[time] = true;
if (Done(time)) {
ans += OK(time);
return;
}
for (int i = 0; i < 5; i++) {
if (time[i] == '?') {
for (int j = 0; j <= 9; j++) {
time[i] = char('0' + j);
DFS(time);
}
return;
}
}
}
int countTime(string time) {
ans = 0;
mp.clear();
DFS(time);
return ans;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 二的幂数组中查询范围内的乘积
- Difficulty: Medium
- Tag:
给你一个正整数 n ,你需要找到一个下标从 0 开始的数组 powers ,它包含 最少 数目的 2 的幂,且它们的和为 n 。powers 数组是 非递减 顺序的。根据前面描述,构造 powers 数组的方法是唯一的。
同时给你一个下标从 0 开始的二维整数数组 queries ,其中 queries[i] = [lefti, righti] ,其中 queries[i] 表示请你求出满足 lefti <= j <= righti 的所有 powers[j] 的乘积。
请你返回一个数组 answers ,长度与 queries 的长度相同,其中 answers[i]是第 i 个查询的答案。由于查询的结果可能非常大,请你将每个 answers[i] 都对 109 + 7 取余 。
示例 1:
输入:n = 15, queries = [[0,1],[2,2],[0,3]]
输出:[2,4,64]
解释:
对于 n = 15 ,得到 powers = [1,2,4,8] 。没法得到元素数目更少的数组。
第 1 个查询的答案:powers[0] * powers[1] = 1 * 2 = 2 。
第 2 个查询的答案:powers[2] = 4 。
第 3 个查询的答案:powers[0] * powers[1] * powers[2] * powers[3] = 1 * 2 * 4 * 8 = 64 。
每个答案对 109 + 7 得到的结果都相同,所以返回 [2,4,64] 。
示例 2:
输入:n = 2, queries = [[0,0]]
输出:[2]
解释:
对于 n = 2, powers = [2] 。
唯一一个查询的答案是 powers[0] = 2 。答案对 109 + 7 取余后结果相同,所以返回 [2] 。
提示:
1 <= n <= 1091 <= queries.length <= 1050 <= starti <= endi < powers.length
Metadata
- Link: Range Product Queries of Powers
- Difficulty: Medium
- Tag:
Given a positive integer n, there exists a 0-indexed array called powers, composed of the minimum number of powers of 2 that sum to n. The array is sorted in non-decreasing order, and there is only one way to form the array.
You are also given a 0-indexed 2D integer array queries, where queries[i] = [lefti, righti]. Each queries[i] represents a query where you have to find the product of all powers[j] with lefti <= j <= righti.
Return an array answers, equal in length to queries, where answers[i] is the answer to the ith query. Since the answer to the ith query may be too large, each answers[i] should be returned modulo 109 + 7.
Example 1:
Input: n = 15, queries = [[0,1],[2,2],[0,3]]
Output: [2,4,64]
Explanation:
For n = 15, powers = [1,2,4,8]. It can be shown that powers cannot be a smaller size.
Answer to 1st query: powers[0] * powers[1] = 1 * 2 = 2.
Answer to 2nd query: powers[2] = 4.
Answer to 3rd query: powers[0] * powers[1] * powers[2] * powers[3] = 1 * 2 * 4 * 8 = 64.
Each answer modulo 109 + 7 yields the same answer, so [2,4,64] is returned.
Example 2:
Input: n = 2, queries = [[0,0]]
Output: [2]
Explanation:
For n = 2, powers = [2].
The answer to the only query is powers[0] = 2. The answer modulo 109 + 7 is the same, so [2] is returned.
Constraints:
1 <= n <= 1091 <= queries.length <= 1050 <= starti <= endi < powers.length
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
constexpr int mod = 1e9 + 7;
class Solution {
public:
vector<int> productQueries(int n, vector<vector<int>> &queries) {
auto f = vector<int>();
int bit = 1;
int _n = n;
while (_n) {
if (_n & 1) {
f.push_back(bit);
}
bit <<= 1;
_n >>= 1;
}
sort(all(f));
auto res = vector<int>();
for (const auto &q : queries) {
int l = q[0];
int r = q[1];
ll cur_res = 1;
for (int i = l; i <= r; i++) {
cur_res = 1ll * cur_res * f[i] % mod;
}
res.push_back(int(cur_res));
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 最小化数组中的最大值
- Difficulty: Medium
- Tag:
给你一个下标从 0 开始的数组 nums ,它含有 n 个非负整数。
每一步操作中,你需要:
- 选择一个满足
1 <= i < n的整数i,且nums[i] > 0。 - 将
nums[i]减 1 。 - 将
nums[i - 1]加 1 。
你可以对数组执行 任意 次上述操作,请你返回可以得到的 nums 数组中 最大值 最小 为多少。
示例 1:
输入:nums = [3,7,1,6]
输出:5
解释:
一串最优操作是:
1. 选择 i = 1 ,nums 变为 [4,6,1,6] 。
2. 选择 i = 3 ,nums 变为 [4,6,2,5] 。
3. 选择 i = 1 ,nums 变为 [5,5,2,5] 。
nums 中最大值为 5 。无法得到比 5 更小的最大值。
所以我们返回 5 。
示例 2:
输入:nums = [10,1]
输出:10
解释:
最优解是不改动 nums ,10 是最大值,所以返回 10 。
提示:
n == nums.length2 <= n <= 1050 <= nums[i] <= 109
Metadata
- Link: Minimize Maximum of Array
- Difficulty: Medium
- Tag:
You are given a 0-indexed array nums comprising of n non-negative integers.
In one operation, you must:
- Choose an integer
isuch that1 <= i < nandnums[i] > 0. - Decrease
nums[i]by 1. - Increase
nums[i - 1]by 1.
Return the minimum possible value of the maximum integer of nums after performing any number of operations.
Example 1:
Input: nums = [3,7,1,6]
Output: 5
Explanation:
One set of optimal operations is as follows:
1. Choose i = 1, and nums becomes [4,6,1,6].
2. Choose i = 3, and nums becomes [4,6,2,5].
3. Choose i = 1, and nums becomes [5,5,2,5].
The maximum integer of nums is 5. It can be shown that the maximum number cannot be less than 5.
Therefore, we return 5.
Example 2:
Input: nums = [10,1]
Output: 10
Explanation:
It is optimal to leave nums as is, and since 10 is the maximum value, we return 10.
Constraints:
n == nums.length2 <= n <= 1050 <= nums[i] <= 109
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int minimizeArrayValue(vector<int> &nums) {
int n = int(nums.size());
const auto OK = [&nums, &n](int mid) {
ll remind = 0;
for (int i = 0; i < n; i++) {
if (nums[i] <= mid) {
remind += mid - nums[i];
} else {
int diff = nums[i] - mid;
if (diff > remind) {
return false;
}
remind -= diff;
}
}
return true;
};
int l = 0, r = 1e9, res = r;
while (r - l >= 0) {
int mid = (l + r) >> 1;
if (OK(mid)) {
res = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 创建价值相同的连通块
- Difficulty: Hard
- Tag:
有一棵 n 个节点的无向树,节点编号为 0 到 n - 1 。
给你一个长度为 n 下标从 0 开始的整数数组 nums ,其中 nums[i] 表示第 i 个节点的值。同时给你一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 与 bi 之间有一条边。
你可以 删除 一些边,将这棵树分成几个连通块。一个连通块的 价值 定义为这个连通块中 所有 节点 i 对应的 nums[i] 之和。
你需要删除一些边,删除后得到的各个连通块的价值都相等。请返回你可以删除的边数 最多 为多少。
示例 1:
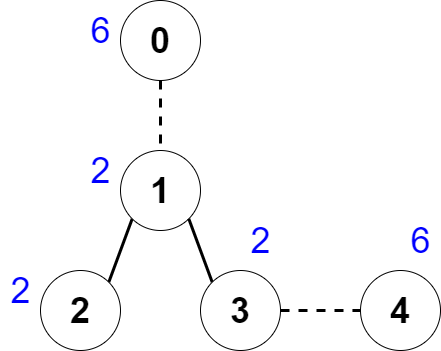
输入:nums = [6,2,2,2,6], edges = [[0,1],[1,2],[1,3],[3,4]]
输出:2
解释:上图展示了我们可以删除边 [0,1] 和 [3,4] 。得到的连通块为 [0] ,[1,2,3] 和 [4] 。每个连通块的价值都为 6 。可以证明没有别的更好的删除方案存在了,所以答案为 2 。
示例 2:
输入:nums = [2], edges = []
输出:0
解释:没有任何边可以删除。
提示:
1 <= n <= 2 * 104nums.length == n1 <= nums[i] <= 50edges.length == n - 1edges[i].length == 20 <= edges[i][0], edges[i][1] <= n - 1edges表示一棵合法的树。
Metadata
- Link: Create Components With Same Value
- Difficulty: Hard
- Tag:
There is an undirected tree with n nodes labeled from 0 to n - 1.
You are given a 0-indexed integer array nums of length n where nums[i] represents the value of the ith node. You are also given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.
You are allowed to delete some edges, splitting the tree into multiple connected components. Let the value of a component be the sum of all nums[i] for which node i is in the component.
Return the maximum number of edges you can delete, such that every connected component in the tree has the same value.
Example 1:

Input: nums = [6,2,2,2,6], edges = [[0,1],[1,2],[1,3],[3,4]]
Output: 2
Explanation: The above figure shows how we can delete the edges [0,1] and [3,4]. The created components are nodes [0], [1,2,3] and [4]. The sum of the values in each component equals 6. It can be proven that no better deletion exists, so the answer is 2.
Example 2:
Input: nums = [2], edges = []
Output: 0
Explanation: There are no edges to be deleted.
Constraints:
1 <= n <= 2 * 104nums.length == n1 <= nums[i] <= 50edges.length == n - 1edges[i].length == 20 <= edges[i][0], edges[i][1] <= n - 1edgesrepresents a valid tree.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
vector<vector<int>> G;
vector<int> nums;
int n, sum, target;
int cnt;
int DFS(int u, int fa) {
int cur = nums[u];
for (const auto &v : G[u]) {
if (v == fa) {
continue;
}
cur += DFS(v, u);
}
if (cur == target) {
++cnt;
cur = 0;
}
return cur;
}
bool OK(int m) {
target = sum / m;
cnt = 0;
DFS(0, 0);
return cnt == m;
}
int componentValue(vector<int> &nums, vector<vector<int>> &edges) {
n = int(nums.size());
G = vector<vector<int>>(n + 1, vector<int>());
this->nums = nums;
for (const auto &e : edges) {
int u = e[0];
int v = e[1];
G[u].push_back(v);
G[v].push_back(u);
}
sum = accumulate(all(nums), 0);
for (int i = min(n, sum); i >= 1; i--) {
if (sum % i != 0) {
continue;
}
if (OK(i)) {
return i - 1;
}
}
return 0;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif