biweekly-contest-73
A
Statement
Metadata
- Link: 数组中紧跟 key 之后出现最频繁的数字
- Difficulty: Easy
- Tag:
给你一个下标从 0 开始的整数数组 nums ,同时给你一个整数 key ,它在 nums 出现过。
统计 在 nums 数组中紧跟着 key 后面出现的不同整数 target 的出现次数。换言之,target 的出现次数为满足以下条件的 i 的数目:
0 <= i <= n - 2nums[i] == key且nums[i + 1] == target。
请你返回出现 最多 次数的 target 。测试数据保证出现次数最多的 target 是唯一的。
示例 1:
输入:nums = [1,100,200,1,100], key = 1
输出:100
解释:对于 target = 100 ,在下标 1 和 4 处出现过 2 次,且都紧跟着 key 。
没有其他整数在 key 后面紧跟着出现,所以我们返回 100 。
示例 2:
输入:nums = [2,2,2,2,3], key = 2
输出:2
解释:对于 target = 2 ,在下标 1 ,2 和 3 处出现过 3 次,且都紧跟着 key 。
对于 target = 3 ,在下标 4 出出现过 1 次,且紧跟着 key 。
target = 2 是紧跟着 key 之后出现次数最多的数字,所以我们返回 2 。
提示:
2 <= nums.length <= 10001 <= nums[i] <= 1000- 测试数据保证答案是唯一的。
Metadata
- Link: Most Frequent Number Following Key In an Array
- Difficulty: Easy
- Tag:
You are given a 0-indexed integer array nums. You are also given an integer key, which is present in nums.
For every unique integer target in nums, count the number of times target immediately follows an occurrence of key in nums. In other words, count the number of indices i such that:
0 <= i <= n - 2,nums[i] == keyand,nums[i + 1] == target.
Return the target with the maximum count. The test cases will be generated such that the target with maximum count is unique.
Example 1:
Input: nums = [1,100,200,1,100], key = 1
Output: 100
Explanation: For target = 100, there are 2 occurrences at indices 1 and 4 which follow an occurrence of key.
No other integers follow an occurrence of key, so we return 100.
Example 2:
Input: nums = [2,2,2,2,3], key = 2
Output: 2
Explanation: For target = 2, there are 3 occurrences at indices 1, 2, and 3 which follow an occurrence of key.
For target = 3, there is only one occurrence at index 4 which follows an occurrence of key.
target = 2 has the maximum number of occurrences following an occurrence of key, so we return 2.
Constraints:
2 <= nums.length <= 10001 <= nums[i] <= 1000- The test cases will be generated such that the answer is unique.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int mostFrequent(vector<int> &nums, int key) {
vector<int> cnt(1005, 0);
int n = nums.size();
for (int i = 0; i < n - 1; i++) {
if (nums[i] == key) {
++cnt[nums[i + 1]];
}
}
int res = 1;
int m = 0;
for (int i = 1; i <= 1000; i++) {
if (cnt[i] > m) {
m = cnt[i];
res = i;
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 将杂乱无章的数字排序
- Difficulty: Medium
- Tag:
排序数组
给你一个下标从 0 开始的整数数组 mapping ,它表示一个十进制数的映射规则,mapping[i] = j 表示这个规则下将数位 i 映射为数位 j 。
一个整数 映射后的值 为将原数字每一个数位 i (0 <= i <= 9)映射为 mapping[i] 。
另外给你一个整数数组 nums ,请你将数组 nums 中每个数按照它们映射后对应数字非递减顺序排序后返回。
注意:
- 如果两个数字映射后对应的数字大小相同,则将它们按照输入中的 相对顺序 排序。
nums中的元素只有在排序的时候需要按照映射后的值进行比较,返回的值应该是输入的元素本身。
示例 1:
输入:mapping = [8,9,4,0,2,1,3,5,7,6], nums = [991,338,38]
输出:[338,38,991]
解释:
将数字 991 按照如下规则映射:
1. mapping[9] = 6 ,所有数位 9 都会变成 6 。
2. mapping[1] = 9 ,所有数位 1 都会变成 8 。
所以,991 映射的值为 669 。
338 映射为 007 ,去掉前导 0 后得到 7 。
38 映射为 07 ,去掉前导 0 后得到 7 。
由于 338 和 38 映射后的值相同,所以它们的前后顺序保留原数组中的相对位置关系,338 在 38 的前面。
所以,排序后的数组为 [338,38,991] 。
示例 2:
输入:mapping = [0,1,2,3,4,5,6,7,8,9], nums = [789,456,123]
输出:[123,456,789]
解释:789 映射为 789 ,456 映射为 456 ,123 映射为 123 。所以排序后数组为 [123,456,789] 。
提示:
mapping.length == 100 <= mapping[i] <= 9mapping[i]的值 互不相同 。1 <= nums.length <= 3 * 1040 <= nums[i] < 109
Metadata
- Link: Sort the Jumbled Numbers
- Difficulty: Medium
- Tag:
SortArray
You are given a 0-indexed integer array mapping which represents the mapping rule of a shuffled decimal system. mapping[i] = j means digit i should be mapped to digit j in this system.
The mapped value of an integer is the new integer obtained by replacing each occurrence of digit i in the integer with mapping[i] for all 0 <= i <= 9.
You are also given another integer array nums. Return the array nums sorted in non-decreasing order based on the mapped values of its elements.
Notes:
- Elements with the same mapped values should appear in the same relative order as in the input.
- The elements of
numsshould only be sorted based on their mapped values and not be replaced by them.
Example 1:
Input: mapping = [8,9,4,0,2,1,3,5,7,6], nums = [991,338,38]
Output: [338,38,991]
Explanation:
Map the number 991 as follows:
1. mapping[9] = 6, so all occurrences of the digit 9 will become 6.
2. mapping[1] = 9, so all occurrences of the digit 1 will become 9.
Therefore, the mapped value of 991 is 669.
338 maps to 007, or 7 after removing the leading zeros.
38 maps to 07, which is also 7 after removing leading zeros.
Since 338 and 38 share the same mapped value, they should remain in the same relative order, so 338 comes before 38.
Thus, the sorted array is [338,38,991].
Example 2:
Input: mapping = [0,1,2,3,4,5,6,7,8,9], nums = [789,456,123]
Output: [123,456,789]
Explanation: 789 maps to 789, 456 maps to 456, and 123 maps to 123. Thus, the sorted array is [123,456,789].
Constraints:
mapping.length == 100 <= mapping[i] <= 9- All the values of
mapping[i]are unique. 1 <= nums.length <= 3 * 1040 <= nums[i] < 109
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T& a, const S& b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T& a, const S& b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
struct node {
int ix;
int v;
int w;
bool operator<(const node& other) const {
if (w != other.w) {
return w < other.w;
}
return ix < other.ix;
}
};
class Solution {
public:
vector<int> sortJumbled(vector<int>& mapping, vector<int>& nums) {
int n = nums.size();
vector<node> vec;
auto f = [&](int x) {
if (x == 0) {
return mapping[0];
}
int res = 0;
int base = 1;
while (x) {
res += mapping[x % 10] * base;
x /= 10;
base *= 10;
}
return res;
};
for (int i = 0; i < n; i++) {
int a = nums[i];
vec.emplace_back(node{
.ix = i,
.v = a,
.w = f(a),
});
}
sort(vec.begin(), vec.end());
vector<int> res;
for (const auto& a : vec) {
res.push_back(a.v);
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 有向无环图中一个节点的所有祖先
- Difficulty: Medium
- Tag:
深度优先搜索广度优先搜索
给你一个正整数 n ,它表示一个 有向无环图 中节点的数目,节点编号为 0 到 n - 1 (包括两者)。
给你一个二维整数数组 edges ,其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。
请你返回一个数组 answer,其中 answer[i]是第 i 个节点的所有 祖先 ,这些祖先节点 升序 排序。
如果 u 通过一系列边,能够到达 v ,那么我们称节点 u 是节点 v 的 祖先 节点。
示例 1:
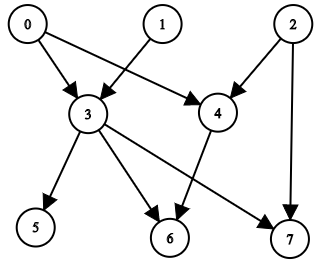
输入:n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
输出:[[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
解释:
上图为输入所对应的图。
- 节点 0 ,1 和 2 没有任何祖先。
- 节点 3 有 2 个祖先 0 和 1 。
- 节点 4 有 2 个祖先 0 和 2 。
- 节点 5 有 3 个祖先 0 ,1 和 3 。
- 节点 6 有 5 个祖先 0 ,1 ,2 ,3 和 4 。
- 节点 7 有 4 个祖先 0 ,1 ,2 和 3 。
示例 2:
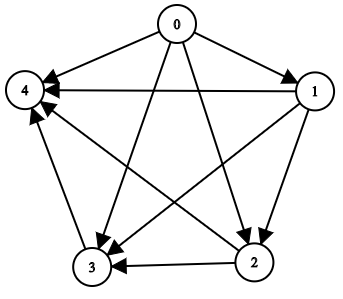
输入:n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
输出:[[],[0],[0,1],[0,1,2],[0,1,2,3]]
解释:
上图为输入所对应的图。
- 节点 0 没有任何祖先。
- 节点 1 有 1 个祖先 0 。
- 节点 2 有 2 个祖先 0 和 1 。
- 节点 3 有 3 个祖先 0 ,1 和 2 。
- 节点 4 有 4 个祖先 0 ,1 ,2 和 3 。
提示:
1 <= n <= 10000 <= edges.length <= min(2000, n * (n - 1) / 2)edges[i].length == 20 <= fromi, toi <= n - 1fromi != toi- 图中不会有重边。
- 图是 有向 且 无环 的。
Metadata
- Link: All Ancestors of a Node in a Directed Acyclic Graph
- Difficulty: Medium
- Tag:
Depth-First SearchBreadth-First Search
You are given a positive integer n representing the number of nodes of a Directed Acyclic Graph (DAG). The nodes are numbered from 0 to n - 1 (inclusive).
You are also given a 2D integer array edges, where edges[i] = [fromi, toi] denotes that there is a unidirectional edge from fromi to toi in the graph.
Return a list answer, where answer[i] is the list of ancestors of the ith node, sorted in ascending order.
A node u is an ancestor of another node v if u can reach v via a set of edges.
Example 1:

Input: n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
Output: [[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Nodes 0, 1, and 2 do not have any ancestors.
- Node 3 has two ancestors 0 and 1.
- Node 4 has two ancestors 0 and 2.
- Node 5 has three ancestors 0, 1, and 3.
- Node 6 has five ancestors 0, 1, 2, 3, and 4.
- Node 7 has four ancestors 0, 1, 2, and 3.
Example 2:

Input: n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
Output: [[],[0],[0,1],[0,1,2],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Node 0 does not have any ancestor.
- Node 1 has one ancestor 0.
- Node 2 has two ancestors 0 and 1.
- Node 3 has three ancestors 0, 1, and 2.
- Node 4 has four ancestors 0, 1, 2, and 3.
Constraints:
1 <= n <= 10000 <= edges.length <= min(2000, n * (n - 1) / 2)edges[i].length == 20 <= fromi, toi <= n - 1fromi != toi- There are no duplicate edges.
- The graph is directed and acyclic.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
vector<int> bfs(int st, int n, const vector<vector<int>> &G) {
vector<int> cnt(n + 1, 0), res;
queue<int> q;
q.push(st);
cnt[st] = 1;
while (!q.empty()) {
int u = q.front();
q.pop();
for (const auto &to : G[u]) {
if (cnt[to]) {
continue;
}
cnt[to] = 1;
q.push(to);
res.push_back(to);
}
}
sort(res.begin(), res.end());
return res;
}
vector<vector<int>> getAncestors(int n, vector<vector<int>> &edges) {
vector<vector<int>> G(n + 5, vector<int>{});
for (const auto &e : edges) {
int u = e[0];
int v = e[1];
G[v].push_back(u);
}
vector<vector<int>> res(n, vector<int>{});
for (int i = 0; i < n; i++) {
res[i] = bfs(i, n, G);
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 得到回文串的最少操作次数
- Difficulty: Hard
- Tag:
贪心
给你一个只包含小写英文字母的字符串 s 。
每一次 操作 ,你可以选择 s 中两个 相邻 的字符,并将它们交换。
请你返回将 s 变成回文串的 最少操作次数 。
注意 ,输入数据会确保 s 一定能变成一个回文串。
示例 1:
输入:s = "aabb"
输出:2
解释:
我们可以将 s 变成 2 个回文串,"abba" 和 "baab" 。
- 我们可以通过 2 次操作得到 "abba" :"aabb" -> "abab" -> "abba" 。
- 我们可以通过 2 次操作得到 "baab" :"aabb" -> "abab" -> "baab" 。
因此,得到回文串的最少总操作次数为 2 。
示例 2:
输入:s = "letelt"
输出:2
解释:
通过 2 次操作从 s 能得到回文串 "lettel" 。
其中一种方法是:"letelt" -> "letetl" -> "lettel" 。
其他回文串比方说 "tleelt" 也可以通过 2 次操作得到。
可以证明少于 2 次操作,无法得到回文串。
提示:
1 <= s.length <= 2000s只包含小写英文字母。s可以通过有限次操作得到一个回文串。
Metadata
- Link: Minimum Number of Moves to Make Palindrome
- Difficulty: Hard
- Tag:
Greedy
You are given a string s consisting only of lowercase English letters.
In one move, you can select any two adjacent characters of s and swap them.
Return the minimum number of moves needed to make s a palindrome.
Note that the input will be generated such that s can always be converted to a palindrome.
Example 1:
Input: s = "aabb"
Output: 2
Explanation:
We can obtain two palindromes from s, "abba" and "baab".
- We can obtain "abba" from s in 2 moves: "aabb" -> "abab" -> "abba".
- We can obtain "baab" from s in 2 moves: "aabb" -> "abab" -> "baab".
Thus, the minimum number of moves needed to make s a palindrome is 2.
Example 2:
Input: s = "letelt"
Output: 2
Explanation:
One of the palindromes we can obtain from s in 2 moves is "lettel".
One of the ways we can obtain it is "letelt" -> "letetl" -> "lettel".
Other palindromes such as "tleelt" can also be obtained in 2 moves.
It can be shown that it is not possible to obtain a palindrome in less than 2 moves.
Constraints:
1 <= s.length <= 2000sconsists only of lowercase English letters.scan be converted to a palindrome using a finite number of moves.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
// ababd
// abdab
// abdba
class Solution {
public:
int minMovesToMakePalindrome(string s) {
int res = 0;
vector<int> cnt(30, 0), use(30, 0);
for (const auto &c : s) {
++cnt[c - 'a'];
}
int n = s.size();
int mid = n / 2;
auto valid = [&](int c) {
return use[c] < cnt[c] / 2;
};
auto _swap = [&](int i, int j) {
for (int k = j; k > i; k--) {
swap(s[k], s[k - 1]);
++res;
}
};
for (int i = 0; i < mid; i++) {
for (int j = i; j < n; j++) {
if (valid(s[j] - 'a')) {
_swap(i, j);
break;
}
}
++use[s[i] - 'a'];
}
if (n & 1) {
int target = 0;
for (int i = 0; i < 26; i++) {
if (cnt[i] & 1) {
target = i;
break;
}
}
for (int i = mid; i < n; i++) {
if (s[i] - 'a' == target) {
_swap(mid, i);
break;
}
}
}
for (int i = (n & 1) ? mid + 1 : mid; i < n; i++) {
int u = s[i], v = s[n - i - 1];
if (u == v) {
continue;
}
for (int j = i; j < n; j++) {
if (s[j] == v) {
_swap(i, j);
break;
}
}
}
// dbg(s);
return res;
}
};
#ifdef LOCAL
int main() {
{
auto s = new Solution();
auto ans = s->minMovesToMakePalindrome("aabb");
dbg(ans);
}
return 0;
}
#endif