weekly-contest-304
A
Statement
Metadata
- Link: 使数组中所有元素都等于零
- Difficulty: Easy
- Tag:
给你一个非负整数数组 nums 。在一步操作中,你必须:
- 选出一个正整数
x,x需要小于或等于nums中 最小 的 非零 元素。 nums中的每个正整数都减去x。
返回使 nums 中所有元素都等于 0 需要的 最少 操作数。
示例 1:
输入:nums = [1,5,0,3,5]
输出:3
解释:
第一步操作:选出 x = 1 ,之后 nums = [0,4,0,2,4] 。
第二步操作:选出 x = 2 ,之后 nums = [0,2,0,0,2] 。
第三步操作:选出 x = 2 ,之后 nums = [0,0,0,0,0] 。示例 2:
输入:nums = [0]
输出:0
解释:nums 中的每个元素都已经是 0 ,所以不需要执行任何操作。
提示:
1 <= nums.length <= 1000 <= nums[i] <= 100
Metadata
- Link: Make Array Zero by Subtracting Equal Amounts
- Difficulty: Easy
- Tag:
You are given a non-negative integer array nums. In one operation, you must:
- Choose a positive integer
xsuch thatxis less than or equal to the smallest non-zero element innums. - Subtract
xfrom every positive element innums.
Return the minimum number of operations to make every element in nums equal to 0.
Example 1:
Input: nums = [1,5,0,3,5]
Output: 3
Explanation:
In the first operation, choose x = 1. Now, nums = [0,4,0,2,4].
In the second operation, choose x = 2. Now, nums = [0,2,0,0,2].
In the third operation, choose x = 2. Now, nums = [0,0,0,0,0].
Example 2:
Input: nums = [0]
Output: 0
Explanation: Each element in nums is already 0 so no operations are needed.
Constraints:
1 <= nums.length <= 1000 <= nums[i] <= 100
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int minimumOperations(vector<int> &nums) {
sort(all(nums));
nums.erase(unique(all(nums)), end(nums));
int res = 0;
for (const auto &a : nums) {
res += (a > 0);
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 分组的最大数量
- Difficulty: Medium
- Tag:
给你一个正整数数组 grades ,表示大学中一些学生的成绩。你打算将 所有 学生分为一些 有序 的非空分组,其中分组间的顺序满足以下全部条件:
- 第
i个分组中的学生总成绩 小于 第(i + 1)个分组中的学生总成绩,对所有组均成立(除了最后一组)。 - 第
i个分组中的学生总数 小于 第(i + 1)个分组中的学生总数,对所有组均成立(除了最后一组)。
返回可以形成的 最大 组数。
示例 1:
输入:grades = [10,6,12,7,3,5]
输出:3
解释:下面是形成 3 个分组的一种可行方法:
- 第 1 个分组的学生成绩为 grades = [12] ,总成绩:12 ,学生数:1
- 第 2 个分组的学生成绩为 grades = [6,7] ,总成绩:6 + 7 = 13 ,学生数:2
- 第 3 个分组的学生成绩为 grades = [10,3,5] ,总成绩:10 + 3 + 5 = 18 ,学生数:3
可以证明无法形成超过 3 个分组。
示例 2:
输入:grades = [8,8]
输出:1
解释:只能形成 1 个分组,因为如果要形成 2 个分组的话,会导致每个分组中的学生数目相等。
提示:
1 <= grades.length <= 1051 <= grades[i] <= 105
Metadata
- Link: Maximum Number of Groups Entering a Competition
- Difficulty: Medium
- Tag:
You are given a positive integer array grades which represents the grades of students in a university. You would like to enter all these students into a competition in ordered non-empty groups, such that the ordering meets the following conditions:
- The sum of the grades of students in the
ithgroup is less than the sum of the grades of students in the(i + 1)thgroup, for all groups (except the last). - The total number of students in the
ithgroup is less than the total number of students in the(i + 1)thgroup, for all groups (except the last).
Return the maximum number of groups that can be formed.
Example 1:
Input: grades = [10,6,12,7,3,5]
Output: 3
Explanation: The following is a possible way to form 3 groups of students:
- 1st group has the students with grades = [12]. Sum of grades: 12. Student count: 1
- 2nd group has the students with grades = [6,7]. Sum of grades: 6 + 7 = 13. Student count: 2
- 3rd group has the students with grades = [10,3,5]. Sum of grades: 10 + 3 + 5 = 18. Student count: 3
It can be shown that it is not possible to form more than 3 groups.
Example 2:
Input: grades = [8,8]
Output: 1
Explanation: We can only form 1 group, since forming 2 groups would lead to an equal number of students in both groups.
Constraints:
1 <= grades.length <= 1051 <= grades[i] <= 105
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int maximumGroups(vector<int> &g) {
sort(all(g));
auto v = vector<pair<ll, int>>();
for (int i = 0; i < int(g.size()); ++i) {
if (int(v.size()) < 2) {
v.emplace_back(g[i], 1);
continue;
}
if (int(v.size()) > 1) {
if (v.end()[-1].fi > v.end()[-2].fi && v.end()[-1].se > v.end()[-2].se) {
v.emplace_back(g[i], 1);
continue;
}
}
v.back().fi += g[i];
++v.back().se;
}
while (v.size() >= 2) {
if (v.end()[-1].fi > v.end()[-2].fi && v.end()[-1].se > v.end()[-2].se) {
break;
}
auto bk = v.back();
v.pop_back();
v.back().fi += bk.fi;
v.back().se += bk.se;
}
return int(v.size());
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: 找到离给定两个节点最近的节点
- Difficulty: Medium
- Tag:
给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,每个节点 至多 有一条出边。
有向图用大小为 n 下标从 0 开始的数组 edges 表示,表示节点 i 有一条有向边指向 edges[i] 。如果节点 i 没有出边,那么 edges[i] == -1 。
同时给你两个节点 node1 和 node2 。
请你返回一个从 node1 和 node2 都能到达节点的编号,使节点 node1 和节点 node2 到这个节点的距离 较大值最小化。如果有多个答案,请返回 最小 的节点编号。如果答案不存在,返回 -1 。
注意 edges 可能包含环。
示例 1:
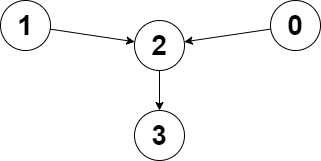
输入:edges = [2,2,3,-1], node1 = 0, node2 = 1
输出:2
解释:从节点 0 到节点 2 的距离为 1 ,从节点 1 到节点 2 的距离为 1 。
两个距离的较大值为 1 。我们无法得到一个比 1 更小的较大值,所以我们返回节点 2 。
示例 2:

输入:edges = [1,2,-1], node1 = 0, node2 = 2
输出:2
解释:节点 0 到节点 2 的距离为 2 ,节点 2 到它自己的距离为 0 。
两个距离的较大值为 2 。我们无法得到一个比 2 更小的较大值,所以我们返回节点 2 。
提示:
n == edges.length2 <= n <= 105-1 <= edges[i] < nedges[i] != i0 <= node1, node2 < n
Metadata
- Link: Find Closest Node to Given Two Nodes
- Difficulty: Medium
- Tag:
You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.
The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from i, then edges[i] == -1.
You are also given two integers node1 and node2.
Return the index of the node that can be reached from both node1 and node2, such that the maximum between the distance from node1 to that node, and from node2 to that node is minimized. If there are multiple answers, return the node with the smallest index, and if no possible answer exists, return -1.
Note that edges may contain cycles.
Example 1:

Input: edges = [2,2,3,-1], node1 = 0, node2 = 1
Output: 2
Explanation: The distance from node 0 to node 2 is 1, and the distance from node 1 to node 2 is 1.
The maximum of those two distances is 1. It can be proven that we cannot get a node with a smaller maximum distance than 1, so we return node 2.
Example 2:

Input: edges = [1,2,-1], node1 = 0, node2 = 2
Output: 2
Explanation: The distance from node 0 to node 2 is 2, and the distance from node 2 to itself is 0.
The maximum of those two distances is 2. It can be proven that we cannot get a node with a smaller maximum distance than 2, so we return node 2.
Constraints:
n == edges.length2 <= n <= 105-1 <= edges[i] < nedges[i] != i0 <= node1, node2 < n
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <queue>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
constexpr int INF = 0x3f3f3f3f;
class Solution {
public:
int closestMeetingNode(vector<int> &e, int node1, int node2) {
int n = int(e.size());
auto bfs = [&n, &e](int st) {
auto dis = vector<int>(n, INF);
dis[st] = 0;
queue<int> q;
q.push(st);
while (!q.empty()) {
int u = q.front();
q.pop();
int nx = e[u];
if (nx == -1) {
continue;
}
if (dis[nx] <= dis[u] + 1) {
continue;
}
q.push(nx);
dis[nx] = dis[u] + 1;
}
return dis;
};
auto dis1 = bfs(node1);
auto dis2 = bfs(node2);
int dis = INF;
int res = -1;
for (int i = 0; i < n; ++i) {
if (dis1[i] == INF || dis2[i] == INF) {
continue;
}
if (chmin(dis, max(dis1[i], dis2[i]))) {
res = i;
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 图中的最长环
- Difficulty: Hard
- Tag:
给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,其中每个节点 至多 有一条出边。
图用一个大小为 n 下标从 0 开始的数组 edges 表示,节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边,那么 edges[i] == -1 。
请你返回图中的 最长 环,如果没有任何环,请返回 -1 。
一个环指的是起点和终点是 同一个 节点的路径。
示例 1:
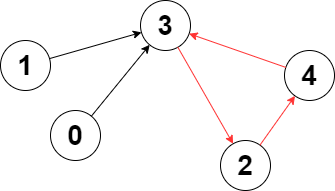
输入:edges = [3,3,4,2,3]
输出去:3
解释:图中的最长环是:2 -> 4 -> 3 -> 2 。
这个环的长度为 3 ,所以返回 3 。
示例 2:
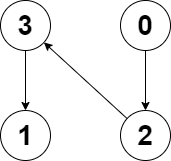
输入:edges = [2,-1,3,1]
输出:-1
解释:图中没有任何环。
提示:
n == edges.length2 <= n <= 105-1 <= edges[i] < nedges[i] != i
Metadata
- Link: Longest Cycle in a Graph
- Difficulty: Hard
- Tag:
You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.
The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from node i, then edges[i] == -1.
Return the length of the longest cycle in the graph. If no cycle exists, return -1.
A cycle is a path that starts and ends at the same node.
Example 1:

Input: edges = [3,3,4,2,3]
Output: 3
Explanation: The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2.
The length of this cycle is 3, so 3 is returned.
Example 2:

Input: edges = [2,-1,3,1]
Output: -1
Explanation: There are no cycles in this graph.
Constraints:
n == edges.length2 <= n <= 105-1 <= edges[i] < nedges[i] != i
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <vector>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int longestCycle(vector<int> &e) {
int n = int(e.size());
auto vis = vector<int>(n, 0);
auto in_sta = vector<int>(n, 0);
int sta_ix = 0;
int res = -1;
auto dfs = [&vis, &in_sta, &sta_ix, &e, &res](auto &&dfs, int u) -> void {
vis[u] = 1;
in_sta[u] = ++sta_ix;
int nx = e[u];
if (nx != -1) {
if (in_sta[nx]) {
int _res = sta_ix - in_sta[nx] + 1;
res = max(res, _res);
}
if (!vis[nx]) {
dfs(dfs, nx);
}
}
in_sta[u] = 0;
--sta_ix;
};
for (int i = 0; i < n; i++) {
if (!vis[i]) {
dfs(dfs, i);
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif