跳转至

675.cut-off-trees-for-golf-event

Statement

Metadata

你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个 m x n 的矩阵表示， 在这个矩阵中：

  • 0 表示障碍，无法触碰
  • 1 表示地面，可以行走
  • 比 1 大的数 表示有树的单元格，可以行走，数值表示树的高度

每一步，你都可以向上、下、左、右四个方向之一移动一个单位，如果你站的地方有一棵树，那么你可以决定是否要砍倒它。

你需要按照树的高度从低向高砍掉所有的树，每砍过一颗树，该单元格的值变为 1（即变为地面）。

你将从 (0, 0) 点开始工作，返回你砍完所有树需要走的最小步数。 如果你无法砍完所有的树，返回 -1 。

可以保证的是，没有两棵树的高度是相同的，并且你至少需要砍倒一棵树。

 

示例 1：

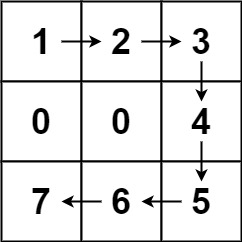
输入：forest = [[1,2,3],[0,0,4],[7,6,5]]
输出：6
解释：沿着上面的路径，你可以用 6 步，按从最矮到最高的顺序砍掉这些树。

示例 2：

输入：forest = [[1,2,3],[0,0,0],[7,6,5]]
输出：-1
解释：由于中间一行被障碍阻塞，无法访问最下面一行中的树。

示例 3：

输入：forest = [[2,3,4],[0,0,5],[8,7,6]]
输出：6
解释：可以按与示例 1 相同的路径来砍掉所有的树。
(0,0) 位置的树，可以直接砍去，不用算步数。

 

提示：

  • m == forest.length
  • n == forest[i].length
  • 1 <= m, n <= 50
  • 0 <= forest[i][j] <= 109

Metadata

You are asked to cut off all the trees in a forest for a golf event. The forest is represented as an m x n matrix. In this matrix:

  • 0 means the cell cannot be walked through.
  • 1 represents an empty cell that can be walked through.
  • A number greater than 1 represents a tree in a cell that can be walked through, and this number is the tree's height.

In one step, you can walk in any of the four directions: north, east, south, and west. If you are standing in a cell with a tree, you can choose whether to cut it off.

You must cut off the trees in order from shortest to tallest. When you cut off a tree, the value at its cell becomes 1 (an empty cell).

Starting from the point (0, 0), return the minimum steps you need to walk to cut off all the trees. If you cannot cut off all the trees, return -1.

You are guaranteed that no two trees have the same height, and there is at least one tree needs to be cut off.

 

Example 1:

Input: forest = [[1,2,3],[0,0,4],[7,6,5]]
Output: 6
Explanation: Following the path above allows you to cut off the trees from shortest to tallest in 6 steps.

Example 2:

Input: forest = [[1,2,3],[0,0,0],[7,6,5]]
Output: -1
Explanation: The trees in the bottom row cannot be accessed as the middle row is blocked.

Example 3:

Input: forest = [[2,3,4],[0,0,5],[8,7,6]]
Output: 6
Explanation: You can follow the same path as Example 1 to cut off all the trees.
Note that you can cut off the first tree at (0, 0) before making any steps.

 

Constraints:

  • m == forest.length
  • n == forest[i].length
  • 1 <= m, n <= 50
  • 0 <= forest[i][j] <= 109

Solution

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair

using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;

using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;

template <typename T, typename S>
inline bool chmax(T& a, const S& b) {
    return a < b ? a = b, 1 : 0;
}

template <typename T, typename S>
inline bool chmin(T& a, const S& b) {
    return a > b ? a = b, 1 : 0;
}

#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head

class Solution {
public:
    int n, m;
    struct node {
        int x, y, v;
        bool operator<(const node& other) const {
            return v < other.v;
        }
    };

    const inline static int dir[][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};

    bool ok(int x, int y) {
        if (x < 0 || x >= n || y < 0 || y >= m) {
            return false;
        }

        return true;
    }

    int bfs(int sx, int sy, int ex, int ey, vector<vector<int>>& f) {
        auto vis = vector<vector<int>>(n + 1, vector<int>(m + 1, 0));
        queue<node> q;
        q.push({.x = sx, .y = sy, .v = 0});
        vis[sx][sy] = 1;

        while (!q.empty()) {
            auto front = q.front();
            q.pop();

            if (front.x == ex && front.y == ey) {
                f[ex][ey] = 1;
                return front.v;
            }

            for (int i = 0; i < 4; i++) {
                int nx = front.x + dir[i][0];
                int ny = front.y + dir[i][1];
                if (ok(nx, ny) && !vis[nx][ny] && f[nx][ny] >= 1) {
                    vis[nx][ny] = 1;
                    q.push({.x = nx, .y = ny, .v = front.v + 1});
                }
            }
        }

        return -1;
    }

    int cutOffTree(vector<vector<int>>& f) {
        n = f.size();
        m = f[0].size();

        auto tree = vector<node>();
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (f[i][j] > 1) {
                    tree.push_back({.x = i, .y = j, .v = f[i][j]});
                }
            }
        }

        sort(tree.begin(), tree.end());

        int sx = 0, sy = 0;
        int res = 0;
        for (const auto& o : tree) {
            int cur = bfs(sx, sy, o.x, o.y, f);
            if (cur == -1) {
                return cur;
            }

            res += cur;
            sx = o.x;
            sy = o.y;
        }

        return res;
    }
};

#ifdef LOCAL

int main() {
    return 0;
}

#endif
最后更新: October 11, 2023
回到页面顶部