weekly-contest-285
A
Statement
Metadata
- Link: 找出数组中的所有 K 近邻下标
- Difficulty: Easy
- Tag:
数组
给你一个下标从 0 开始的整数数组 nums 和两个整数 key 和 k 。K 近邻下标 是 nums 中的一个下标 i ,并满足至少存在一个下标 j 使得 |i - j| <= k 且 nums[j] == key 。
以列表形式返回按 递增顺序 排序的所有 K 近邻下标。
示例 1:
输入:nums = [3,4,9,1,3,9,5], key = 9, k = 1
输出:[1,2,3,4,5,6]
解释:因此,nums[2] == key 且 nums[5] == key 。
- 对下标 0 ,|0 - 2| > k 且 |0 - 5| > k ,所以不存在 j 使得 |0 - j| <= k 且 nums[j] == key 。所以 0 不是一个 K 近邻下标。
- 对下标 1 ,|1 - 2| <= k 且 nums[2] == key ,所以 1 是一个 K 近邻下标。
- 对下标 2 ,|2 - 2| <= k 且 nums[2] == key ,所以 2 是一个 K 近邻下标。
- 对下标 3 ,|3 - 2| <= k 且 nums[2] == key ,所以 3 是一个 K 近邻下标。
- 对下标 4 ,|4 - 5| <= k 且 nums[5] == key ,所以 4 是一个 K 近邻下标。
- 对下标 5 ,|5 - 5| <= k 且 nums[5] == key ,所以 5 是一个 K 近邻下标。
- 对下标 6 ,|6 - 5| <= k 且 nums[5] == key ,所以 6 是一个 K 近邻下标。
因此,按递增顺序返回 [1,2,3,4,5,6] 。
示例 2:
输入:nums = [2,2,2,2,2], key = 2, k = 2
输出:[0,1,2,3,4]
解释:对 nums 的所有下标 i ,总存在某个下标 j 使得 |i - j| <= k 且 nums[j] == key ,所以每个下标都是一个 K 近邻下标。
因此,返回 [0,1,2,3,4] 。
提示:
1 <= nums.length <= 10001 <= nums[i] <= 1000key是数组nums中的一个整数1 <= k <= nums.length
Metadata
- Link: Find All K-Distant Indices in an Array
- Difficulty: Easy
- Tag:
Array
You are given a 0-indexed integer array nums and two integers key and k. A k-distant index is an index i of nums for which there exists at least one index j such that |i - j| <= k and nums[j] == key.
Return a list of all k-distant indices sorted in increasing order.
Example 1:
Input: nums = [3,4,9,1,3,9,5], key = 9, k = 1
Output: [1,2,3,4,5,6]
Explanation: Here, nums[2] == key and nums[5] == key.
- For index 0, |0 - 2| > k and |0 - 5| > k, so there is no j where |0 - j| <= k and nums[j] == key. Thus, 0 is not a k-distant index.
- For index 1, |1 - 2| <= k and nums[2] == key, so 1 is a k-distant index.
- For index 2, |2 - 2| <= k and nums[2] == key, so 2 is a k-distant index.
- For index 3, |3 - 2| <= k and nums[2] == key, so 3 is a k-distant index.
- For index 4, |4 - 5| <= k and nums[5] == key, so 4 is a k-distant index.
- For index 5, |5 - 5| <= k and nums[5] == key, so 5 is a k-distant index.
- For index 6, |6 - 5| <= k and nums[5] == key, so 6 is a k-distant index.
Thus, we return [1,2,3,4,5,6] which is sorted in increasing order.
Example 2:
Input: nums = [2,2,2,2,2], key = 2, k = 2
Output: [0,1,2,3,4]
Explanation: For all indices i in nums, there exists some index j such that |i - j| <= k and nums[j] == key, so every index is a k-distant index.
Hence, we return [0,1,2,3,4].
Constraints:
1 <= nums.length <= 10001 <= nums[i] <= 1000keyis an integer from the arraynums.1 <= k <= nums.length
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int countHillValley(vector<int> &nums) {
int res = 0;
vector<int> a;
for (auto &c : nums) {
if (a.empty())
a.push_back(c);
else if (c != a.back())
a.push_back(c);
}
int n = a.size();
for (int i = 1; i < n - 1; i++) {
int aa = a[i];
int b = a[i - 1];
int c = a[i + 1];
if (b < aa && c < aa)
++res;
if (b > aa && c > aa)
++res;
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
B
Statement
Metadata
- Link: 统计可以提取的工件
- Difficulty: Medium
- Tag:
数组哈希表模拟
存在一个 n x n 大小、下标从 0 开始的网格,网格中埋着一些工件。给你一个整数 n 和一个下标从 0 开始的二维整数数组 artifacts ,artifacts 描述了矩形工件的位置,其中 artifacts[i] = [r1i, c1i, r2i, c2i] 表示第 i 个工件在子网格中的填埋情况:
(r1i, c1i)是第i个工件 左上 单元格的坐标,且(r2i, c2i)是第i个工件 右下 单元格的坐标。
你将会挖掘网格中的一些单元格,并清除其中的填埋物。如果单元格中埋着工件的一部分,那么该工件这一部分将会裸露出来。如果一个工件的所有部分都都裸露出来,你就可以提取该工件。
给你一个下标从 0 开始的二维整数数组 dig ,其中 dig[i] = [ri, ci] 表示你将会挖掘单元格 (ri, ci) ,返回你可以提取的工件数目。
生成的测试用例满足:
- 不存在重叠的两个工件。
- 每个工件最多只覆盖
4个单元格。 dig中的元素互不相同。
示例 1:
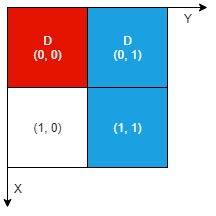
输入:n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1]]
输出:1
解释:
不同颜色表示不同的工件。挖掘的单元格用 'D' 在网格中进行标记。
有 1 个工件可以提取,即红色工件。
蓝色工件在单元格 (1,1) 的部分尚未裸露出来,所以无法提取该工件。
因此,返回 1 。
示例 2:
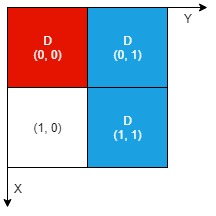
输入:n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1],[1,1]]
输出:2
解释:红色工件和蓝色工件的所有部分都裸露出来(用 'D' 标记),都可以提取。因此,返回 2 。
提示:
1 <= n <= 10001 <= artifacts.length, dig.length <= min(n2, 105)artifacts[i].length == 4dig[i].length == 20 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1r1i <= r2ic1i <= c2i- 不存在重叠的两个工件
- 每个工件 最多 只覆盖
4个单元格 dig中的元素互不相同
Metadata
- Link: Count Artifacts That Can Be Extracted
- Difficulty: Medium
- Tag:
ArrayHash TableSimulation
There is an n x n 0-indexed grid with some artifacts buried in it. You are given the integer n and a 0-indexed 2D integer array artifacts describing the positions of the rectangular artifacts where artifacts[i] = [r1i, c1i, r2i, c2i] denotes that the ith artifact is buried in the subgrid where:
(r1i, c1i)is the coordinate of the top-left cell of theithartifact and(r2i, c2i)is the coordinate of the bottom-right cell of theithartifact.
You will excavate some cells of the grid and remove all the mud from them. If the cell has a part of an artifact buried underneath, it will be uncovered. If all the parts of an artifact are uncovered, you can extract it.
Given a 0-indexed 2D integer array dig where dig[i] = [ri, ci] indicates that you will excavate the cell (ri, ci), return the number of artifacts that you can extract.
The test cases are generated such that:
- No two artifacts overlap.
- Each artifact only covers at most
4cells. - The entries of
digare unique.
Example 1:

Input: n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1]]
Output: 1
Explanation:
The different colors represent different artifacts. Excavated cells are labeled with a 'D' in the grid.
There is 1 artifact that can be extracted, namely the red artifact.
The blue artifact has one part in cell (1,1) which remains uncovered, so we cannot extract it.
Thus, we return 1.
Example 2:

Input: n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1],[1,1]]
Output: 2
Explanation: Both the red and blue artifacts have all parts uncovered (labeled with a 'D') and can be extracted, so we return 2.
Constraints:
1 <= n <= 10001 <= artifacts.length, dig.length <= min(n2, 105)artifacts[i].length == 4dig[i].length == 20 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1r1i <= r2ic1i <= c2i- No two artifacts will overlap.
- The number of cells covered by an artifact is at most
4. - The entries of
digare unique.
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
int countCollisions(string directions) {
int res = 0;
int s = 0;
int r = 0;
for (auto &c : directions) {
if (c == 'S') {
if (r)
res += r;
r = 0;
s = 1;
} else if (c == 'L') {
if (r) {
res += 1 + r;
r = 0;
s = 1;
} else if (s) {
res += 1;
s = 1;
}
} else {
s = 0;
++r;
}
}
return res;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
C
Statement
Metadata
- Link: K 次操作后最大化顶端元素
- Difficulty: Medium
- Tag:
贪心数组
给你一个下标从 0 开始的整数数组 nums ,它表示一个 栈 ,其中 nums[0] 是栈顶的元素。
每一次操作中,你可以执行以下操作 之一 :
- 如果栈非空,那么 删除 栈顶端的元素。
- 如果存在 1 个或者多个被删除的元素,你可以从它们中选择任何一个,添加 回栈顶,这个元素成为新的栈顶元素。
同时给你一个整数 k ,它表示你总共需要执行操作的次数。
请你返回 恰好 执行 k 次操作以后,栈顶元素的 最大值 。如果执行完 k 次操作以后,栈一定为空,请你返回 -1 。
示例 1:
输入:nums = [5,2,2,4,0,6], k = 4
输出:5
解释:
4 次操作后,栈顶元素为 5 的方法之一为:
- 第 1 次操作:删除栈顶元素 5 ,栈变为 [2,2,4,0,6] 。
- 第 2 次操作:删除栈顶元素 2 ,栈变为 [2,4,0,6] 。
- 第 3 次操作:删除栈顶元素 2 ,栈变为 [4,0,6] 。
- 第 4 次操作:将 5 添加回栈顶,栈变为 [5,4,0,6] 。
注意,这不是最后栈顶元素为 5 的唯一方式。但可以证明,4 次操作以后 5 是能得到的最大栈顶元素。
示例 2:
输入:nums = [2], k = 1
输出:-1
解释:
第 1 次操作中,我们唯一的选择是将栈顶元素弹出栈。
由于 1 次操作后无法得到一个非空的栈,所以我们返回 -1 。
提示:
1 <= nums.length <= 1050 <= nums[i], k <= 109
Metadata
- Link: Maximize the Topmost Element After K Moves
- Difficulty: Medium
- Tag:
GreedyArray
You are given a 0-indexed integer array nums representing the contents of a pile, where nums[0] is the topmost element of the pile.
In one move, you can perform either of the following:
- If the pile is not empty, remove the topmost element of the pile.
- If there are one or more removed elements, add any one of them back onto the pile. This element becomes the new topmost element.
You are also given an integer k, which denotes the total number of moves to be made.
Return the maximum value of the topmost element of the pile possible after exactly k moves. In case it is not possible to obtain a non-empty pile after k moves, return -1.
Example 1:
Input: nums = [5,2,2,4,0,6], k = 4
Output: 5
Explanation:
One of the ways we can end with 5 at the top of the pile after 4 moves is as follows:
- Step 1: Remove the topmost element = 5. The pile becomes [2,2,4,0,6].
- Step 2: Remove the topmost element = 2. The pile becomes [2,4,0,6].
- Step 3: Remove the topmost element = 2. The pile becomes [4,0,6].
- Step 4: Add 5 back onto the pile. The pile becomes [5,4,0,6].
Note that this is not the only way to end with 5 at the top of the pile. It can be shown that 5 is the largest answer possible after 4 moves.
Example 2:
Input: nums = [2], k = 1
Output: -1
Explanation:
In the first move, our only option is to pop the topmost element of the pile.
Since it is not possible to obtain a non-empty pile after one move, we return -1.
Constraints:
1 <= nums.length <= 1050 <= nums[i], k <= 109
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
class Solution {
public:
vector<int> maximumBobPoints(int numArrows, vector<int> &aliceArrows) {
int n = 12;
int res = 0;
vector<int> ress = vector<int>(n, 0);
for (int S = 0; S < (1 << 12); S++) {
int tot = numArrows;
int tmpres = 0;
vector<int> tmpress = vector<int>(n, 0);
for (int i = 0; i < 12; i++) {
if ((S >> i) & 1) {
tmpres += i;
tmpress[i] = aliceArrows[i] + 1;
tot -= tmpress[i];
}
}
if (tot < 0) {
continue;
}
if (tot > 0) {
tmpress[0] += tot;
}
if (tmpres > res) {
res = tmpres;
ress.swap(tmpress);
}
}
return ress;
}
};
#ifdef LOCAL
int main() {
return 0;
}
#endif
D
Statement
Metadata
- Link: 得到要求路径的最小带权子图
- Difficulty: Hard
- Tag:
图最短路
给你一个整数 n ,它表示一个 带权有向 图的节点数,节点编号为 0 到 n - 1 。
同时给你一个二维整数数组 edges ,其中 edges[i] = [fromi, toi, weighti] ,表示从 fromi 到 toi 有一条边权为 weighti 的 有向 边。
最后,给你三个 互不相同 的整数 src1 ,src2 和 dest ,表示图中三个不同的点。
请你从图中选出一个 边权和最小 的子图,使得从 src1 和 src2 出发,在这个子图中,都 可以 到达 dest 。如果这样的子图不存在,请返回 -1 。
子图 中的点和边都应该属于原图的一部分。子图的边权和定义为它所包含的所有边的权值之和。
示例 1:
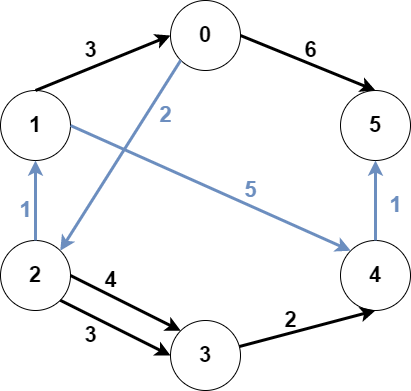
输入:n = 6, edges = [[0,2,2],[0,5,6],[1,0,3],[1,4,5],[2,1,1],[2,3,3],[2,3,4],[3,4,2],[4,5,1]], src1 = 0, src2 = 1, dest = 5
输出:9
解释:
上图为输入的图。
蓝色边为最优子图之一。
注意,子图 [[1,0,3],[0,5,6]] 也能得到最优解,但无法在满足所有限制的前提下,得到更优解。
示例 2:

输入:n = 3, edges = [[0,1,1],[2,1,1]], src1 = 0, src2 = 1, dest = 2
输出:-1
解释:
上图为输入的图。
可以看到,不存在从节点 1 到节点 2 的路径,所以不存在任何子图满足所有限制。
提示:
3 <= n <= 1050 <= edges.length <= 105edges[i].length == 30 <= fromi, toi, src1, src2, dest <= n - 1fromi != toisrc1,src2和dest两两不同。1 <= weight[i] <= 105
Metadata
- Link: Minimum Weighted Subgraph With the Required Paths
- Difficulty: Hard
- Tag:
GraphShortest Path
You are given an integer n denoting the number of nodes of a weighted directed graph. The nodes are numbered from 0 to n - 1.
You are also given a 2D integer array edges where edges[i] = [fromi, toi, weighti] denotes that there exists a directed edge from fromi to toi with weight weighti.
Lastly, you are given three distinct integers src1, src2, and dest denoting three distinct nodes of the graph.
Return the minimum weight of a subgraph of the graph such that it is possible to reach dest from both src1 and src2 via a set of edges of this subgraph. In case such a subgraph does not exist, return -1.
A subgraph is a graph whose vertices and edges are subsets of the original graph. The weight of a subgraph is the sum of weights of its constituent edges.
Example 1:

Input: n = 6, edges = [[0,2,2],[0,5,6],[1,0,3],[1,4,5],[2,1,1],[2,3,3],[2,3,4],[3,4,2],[4,5,1]], src1 = 0, src2 = 1, dest = 5
Output: 9
Explanation:
The above figure represents the input graph.
The blue edges represent one of the subgraphs that yield the optimal answer.
Note that the subgraph [[1,0,3],[0,5,6]] also yields the optimal answer. It is not possible to get a subgraph with less weight satisfying all the constraints.
Example 2:

Input: n = 3, edges = [[0,1,1],[2,1,1]], src1 = 0, src2 = 1, dest = 2
Output: -1
Explanation:
The above figure represents the input graph.
It can be seen that there does not exist any path from node 1 to node 2, hence there are no subgraphs satisfying all the constraints.
Constraints:
3 <= n <= 1050 <= edges.length <= 105edges[i].length == 30 <= fromi, toi, src1, src2, dest <= n - 1fromi != toisrc1,src2, anddestare pairwise distinct.1 <= weight[i] <= 105
Solution
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define endl "\n"
#define fi first
#define se second
#define all(x) begin(x), end(x)
#define rall rbegin(a), rend(a)
#define bitcnt(x) (__builtin_popcountll(x))
#define complete_unique(a) a.erase(unique(begin(a), end(a)), end(a))
#define mst(x, a) memset(x, a, sizeof(x))
#define MP make_pair
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using VLL = std::vector<ll>;
using VI = std::vector<int>;
using PII = std::pair<int, int>;
using PLL = std::pair<ll, ll>;
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
const ll mod = 1e9 + 7;
template <typename T, typename S>
inline bool chmax(T &a, const S &b) {
return a < b ? a = b, 1 : 0;
}
template <typename T, typename S>
inline bool chmin(T &a, const S &b) {
return a > b ? a = b, 1 : 0;
}
#ifdef LOCAL
#include <debug.hpp>
#else
#define dbg(...)
#endif
// head
struct SEG {
static const int N = 100005;
struct node {
int m, lazy;
node() {
m = lazy = 0;
}
void init() {
m = lazy = 0;
}
void up(int x) {
m += x;
lazy += x;
}
node operator+(const node &other) const {
node res = node();
res.m = max(m, other.m);
return res;
}
} t[N << 2], res;
void down(int id) {
int &lazy = t[id].lazy;
t[id << 1].up(lazy);
t[id << 1 | 1].up(lazy);
lazy = 0;
}
void build(int id, int l, int r, const vector<int> &a) {
t[id] = node();
if (l > r) {
return;
}
if (l == r) {
t[id].m = a[l];
return;
}
int mid = (l + r) >> 1;
build(id << 1, l, mid, a);
build(id << 1 | 1, mid + 1, r, a);
t[id] = t[id << 1] + t[id << 1 | 1];
}
void update(int id, int l, int r, int ql, int qr, int v) {
if (ql > qr || ql > r || qr < l) {
return;
}
if (l >= ql && r <= qr) {
t[id].up(v);
return;
}
int mid = (l + r) >> 1;
down(id);
if (ql <= mid)
update(id << 1, l, mid, ql, qr, v);
if (qr > mid)
update(id << 1 | 1, mid + 1, r, ql, qr, v);
t[id] = t[id << 1] + t[id << 1 | 1];
}
void query(int id, int l, int r, int ql, int qr) {
if (ql > qr || ql > r || qr < l) {
return;
}
if (l >= ql && r <= qr) {
res = res + t[id];
return;
}
int mid = (l + r) >> 1;
down(id);
if (ql <= mid)
query(id << 1, l, mid, ql, qr);
if (qr > mid)
query(id << 1 | 1, mid + 1, r, ql, qr);
}
int query(int n, int ix) {
if (ix > n) {
return 0;
}
if (ix < 0) {
return 0;
}
res.init();
query(1, 1, n, ix, ix);
return res.m;
}
};
SEG pre_seg, nx_seg;
class Solution {
public:
vector<int> longestRepeating(string s, string queryCharacters, vector<int> &queryIndices) {
int n = s.length();
s.insert(0, "@");
s.push_back('@');
vector<int> pre(n + 5, 0), nx(n + 5, 0);
pre[0] = 0;
for (int i = 1; i <= n; i++) {
char c = s[i];
char prec = s[i - 1];
if (c == prec) {
pre[i] = pre[i - 1] + 1;
} else {
pre[i] = 1;
}
}
nx[n + 1] = 0;
for (int i = n; i >= 1; i--) {
char c = s[i];
char nxc = s[i + 1];
if (c == nxc) {
nx[i] = nx[i + 1] + 1;
} else {
nx[i] = 1;
}
}
pre_seg.build(1, 1, n, pre);
nx_seg.build(1, 1, n, nx);
vector<int> res;
int k = queryCharacters.length();
for (int i = 0; i < k; i++) {
int ix = queryIndices[i] + 1;
char change_c = queryCharacters[i];
char ori_c = s[ix];
char pre_c = s[ix - 1];
char nx_c = s[ix + 1];
s[ix] = change_c;
if (change_c != ori_c) {
{
int cur_pre = pre_seg.query(n, ix);
int cur_nx = nx_seg.query(n, ix);
nx_seg.update(1, 1, n, ix - cur_pre + 1, ix, -cur_nx);
pre_seg.update(1, 1, n, ix, ix + cur_nx - 1, -cur_pre);
}
{
int ccur_pre = pre_seg.query(n, ix - 1);
int ccur_nx = nx_seg.query(n, ix + 1);
int cur_pre = 1;
int cur_nx = 1;
if (change_c == pre_c) {
cur_pre += ccur_pre;
}
if (change_c == nx_c) {
cur_nx += ccur_nx;
}
nx_seg.update(1, 1, n, ix - cur_pre + 1, ix, cur_nx);
pre_seg.update(1, 1, n, ix, ix + cur_nx - 1, cur_pre);
}
}
pre_seg.res.init();
pre_seg.query(1, 1, n, 1, n);
res.push_back(pre_seg.res.m);
}
return res;
}
};
#ifdef LOCAL
int main() {
{
auto s = new Solution();
auto v = vector<int>({1, 3, 3});
auto ans = s->longestRepeating("babacc", "bcb", v);
dbg(ans);
}
{
auto s = new Solution();
auto v = vector<int>({2, 1});
auto ans = s->longestRepeating("abyzz", "aa", v);
dbg(ans);
}
{
auto s = new Solution();
auto v = vector<int>({5, 0});
auto ans = s->longestRepeating("dbgmcagale", "mf", v);
dbg(ans);
}
return 0;
}
#endif